Question Number 79374 by TawaTawa last updated on 24/Jan/20

Answered by mind is power last updated on 24/Jan/20

$${cv}\:\sim\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\:{Riemann} \\ $$$$\frac{{n}−\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}=\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{−\mathrm{3}}{−\mathrm{1}.\mathrm{1}.\left({n}+\mathrm{2}\right)}−\frac{\mathrm{4}}{\left(−\mathrm{2}\right)\left(−\mathrm{1}\right)\left({n}+\mathrm{3}\right)} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\left\{−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{3}}{\left({n}+\mathrm{2}\right)}−\frac{\mathrm{2}}{\left({n}+\mathrm{3}\right)}\right\} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)+\mathrm{2}\Sigma\left(\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right) \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}+…….\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Sigma\left(\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right)=\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{5}}+…..\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}.\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{6}}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{n}−\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$
Commented by TawaTawa last updated on 24/Jan/20
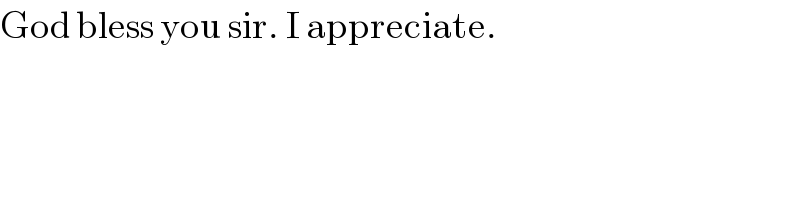
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by mind is power last updated on 24/Jan/20
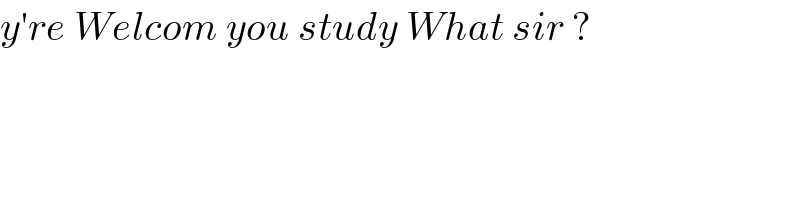
$${y}'{re}\:{Welcom}\:{you}\:{study}\:{What}\:{sir}\:? \\ $$
Commented by TawaTawa last updated on 25/Jan/20

$$\mathrm{Am}\:\mathrm{a}\:\mathrm{girl} \\ $$
Commented by TawaTawa last updated on 25/Jan/20
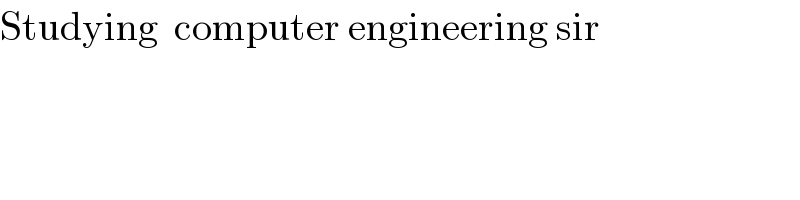
$$\mathrm{Studying}\:\:\mathrm{computer}\:\mathrm{engineering}\:\mathrm{sir} \\ $$
Commented by mind is power last updated on 25/Jan/20
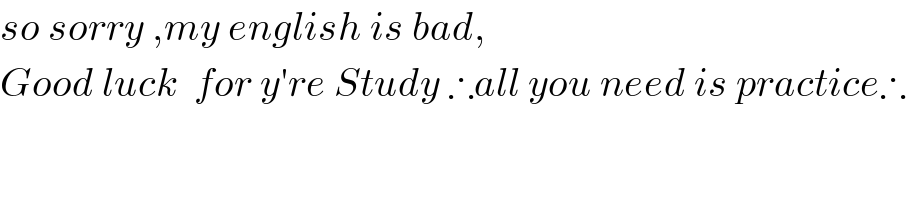
$${so}\:{sorry}\:,{my}\:{english}\:{is}\:{bad}, \\ $$$${Good}\:{luck}\:\:{for}\:{y}'{re}\:{Study}\:\therefore{all}\:{you}\:{need}\:{is}\:{practice}\therefore \\ $$
Commented by TawaTawa last updated on 25/Jan/20

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by TawaTawa last updated on 25/Jan/20
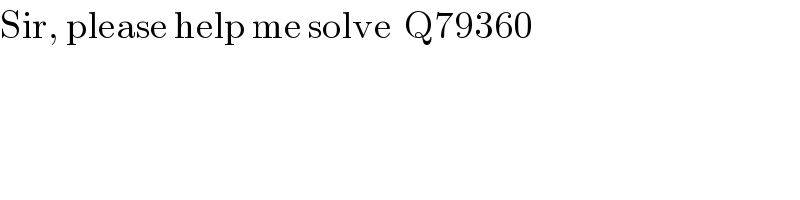
$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{solve}\:\:\mathrm{Q79360} \\ $$
