Question Number 79394 by TawaTawa last updated on 24/Jan/20

Answered by john santu last updated on 25/Jan/20
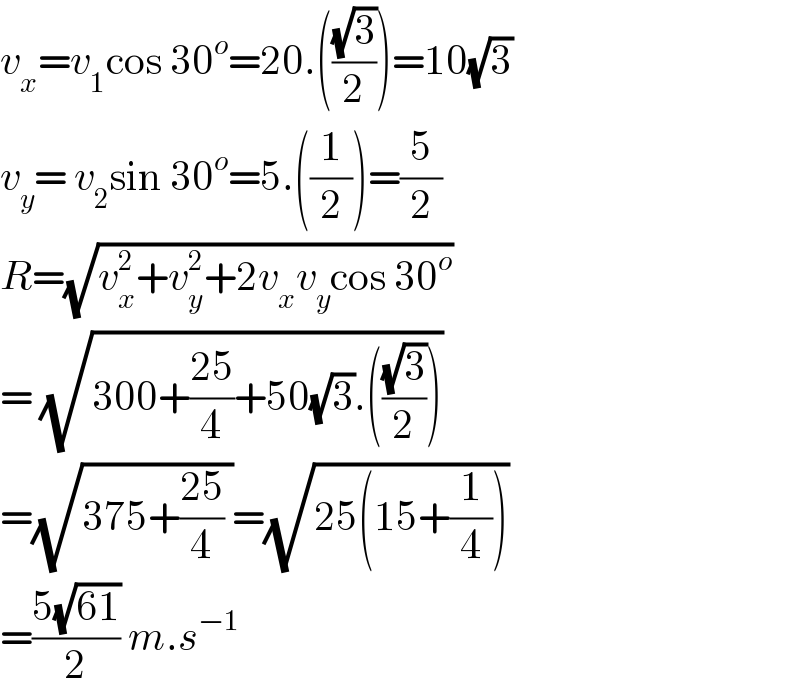
$${v}_{{x}} ={v}_{\mathrm{1}} \mathrm{cos}\:\mathrm{30}^{{o}} =\mathrm{20}.\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\mathrm{10}\sqrt{\mathrm{3}}\: \\ $$$${v}_{{y}} =\:{v}_{\mathrm{2}} \mathrm{sin}\:\mathrm{30}^{{o}} =\mathrm{5}.\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${R}=\sqrt{{v}_{{x}} ^{\mathrm{2}} +{v}_{{y}} ^{\mathrm{2}} +\mathrm{2}{v}_{{x}} {v}_{{y}} \mathrm{cos}\:\mathrm{30}^{{o}} } \\ $$$$=\:\sqrt{\mathrm{300}+\frac{\mathrm{25}}{\mathrm{4}}+\mathrm{50}\sqrt{\mathrm{3}}.\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} \\ $$$$=\sqrt{\mathrm{375}+\frac{\mathrm{25}}{\mathrm{4}}\:}=\sqrt{\mathrm{25}\left(\mathrm{15}+\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$=\frac{\mathrm{5}\sqrt{\mathrm{61}}}{\mathrm{2}}\:{m}.{s}^{−\mathrm{1}} \\ $$
Commented by TawaTawa last updated on 25/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
