Question Number 79413 by rajesh4661kumar@gmail.com last updated on 25/Jan/20
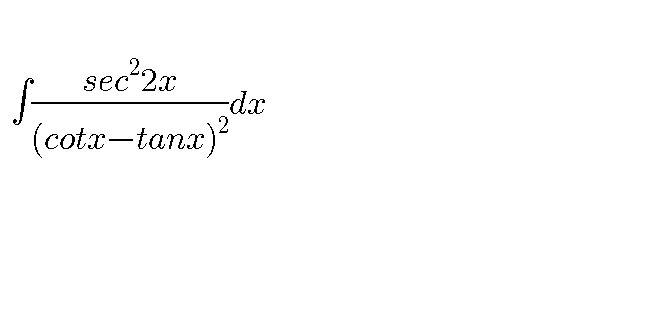
Commented by john santu last updated on 25/Jan/20
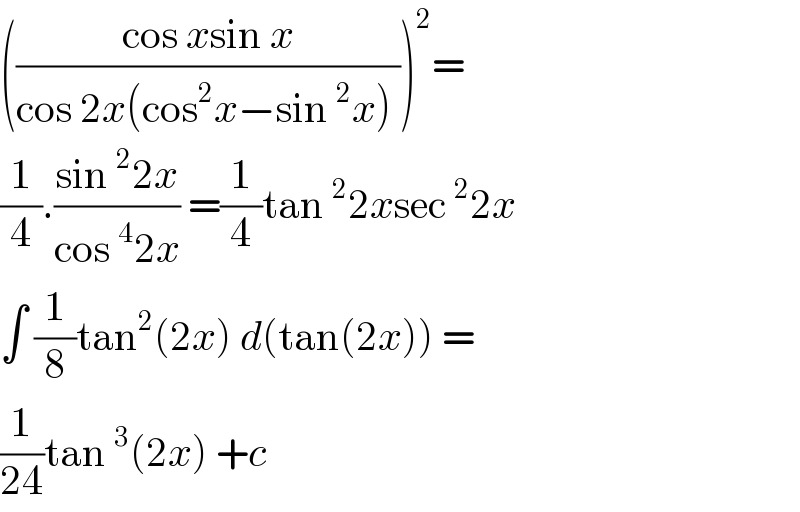
$$\left(\frac{\mathrm{cos}\:{x}\mathrm{sin}\:{x}}{\mathrm{cos}\:\mathrm{2}{x}\left(\mathrm{cos}^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)\:}\right)^{\mathrm{2}} = \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{cos}\:^{\mathrm{4}} \mathrm{2}{x}}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}\:^{\mathrm{2}} \mathrm{2}{x}\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}{x} \\ $$$$\int\:\frac{\mathrm{1}}{\mathrm{8}}\mathrm{tan}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\:{d}\left(\mathrm{tan}\left(\mathrm{2}{x}\right)\right)\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{24}}\mathrm{tan}\:^{\mathrm{3}} \left(\mathrm{2}{x}\right)\:+{c}\: \\ $$
