Question Number 79449 by mr W last updated on 25/Jan/20
Commented by mr W last updated on 25/Jan/20
![[Repost of an old question from b.e.h.i. sir] Find the radius of 20th circle.](https://www.tinkutara.com/question/Q79450.png)
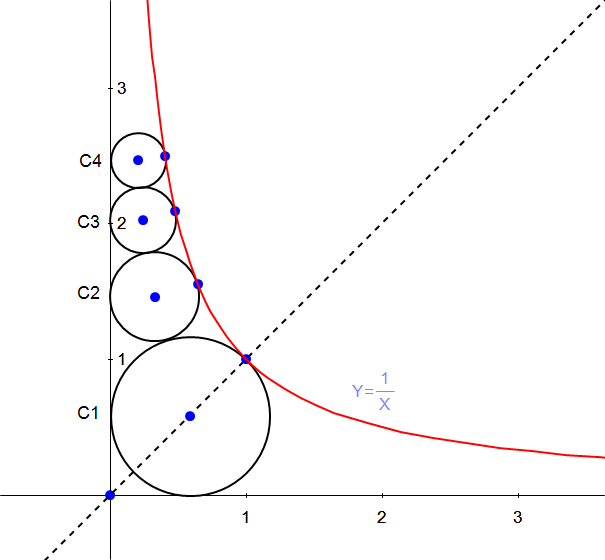
$$\left[{Repost}\:{of}\:{an}\:{old}\:{question}\:{from}\:{b}.{e}.{h}.{i}.\:{sir}\right] \\ $$$${Find}\:{the}\:{radius}\:{of}\:\mathrm{20}{th}\:{circle}. \\ $$
Commented by MJS last updated on 25/Jan/20
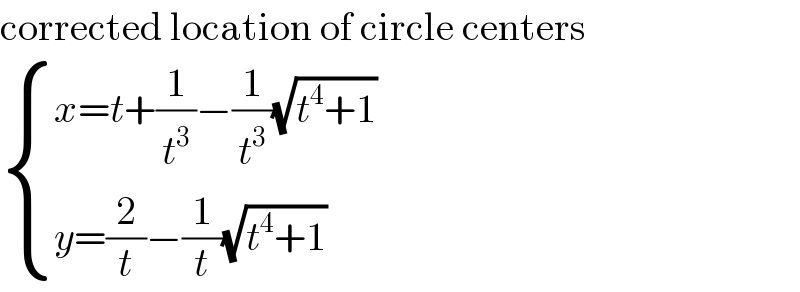
$$\mathrm{corrected}\:\mathrm{location}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{centers} \\ $$$$\begin{cases}{{x}={t}+\frac{\mathrm{1}}{{t}^{\mathrm{3}} }−\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\sqrt{{t}^{\mathrm{4}} +\mathrm{1}}}\\{{y}=\frac{\mathrm{2}}{{t}}−\frac{\mathrm{1}}{{t}}\sqrt{{t}^{\mathrm{4}} +\mathrm{1}}}\end{cases} \\ $$
Commented by john santu last updated on 25/Jan/20

$${waw}…. \\ $$
Commented by MJS last updated on 25/Jan/20

$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake},\:\mathrm{I}'\mathrm{ll}\:\mathrm{post}\:\mathrm{a}\:\mathrm{corrected} \\ $$$$\mathrm{version}\:\mathrm{soon} \\ $$
Commented by MJS last updated on 25/Jan/20
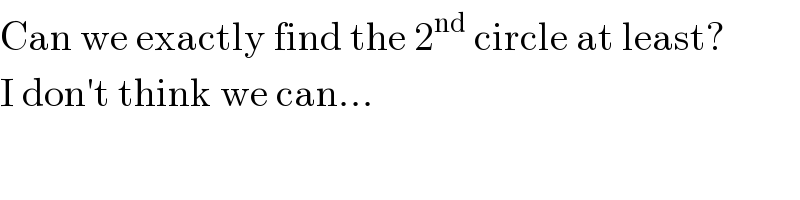
$$\mathrm{Can}\:\mathrm{we}\:\mathrm{exactly}\:\mathrm{find}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{circle}\:\mathrm{at}\:\mathrm{least}? \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}… \\ $$
Commented by MJS last updated on 25/Jan/20
![one possible path, but no exact solution center of C_n =M_n = (((t_n +(1/t_n ^3 )−(1/t_n ^3 )(√(t_n ^4 +1)))),(((2/t_n )−(1/t_n )(√(t_n ^4 +1)))) ) radius of C_n =r_n =t_n +(1/t_n ^3 )−(1/t_n ^3 )(√(t_n ^4 +1)) [t_1 =1 ⇒ M_1 = (((2−(√2))),((2−(√2))) ) ∧ r_1 =2−(√2)] ∣C_n C_(n+1) ∣^2 =(r_n +r_(n+1) )^2 starting with n=1 let t_2 =p (((4−2(√2))/p)−(6/p^2 )+((4−2(√2))/p^3 )−(2/p^6 ))(√(p^4 +1))+2p^2 −(4−2(√2))p−((8−4(√2))/p)+(8/p^2 )−((4−2(√2))/p^3 )+(2/p^6 )+12−8(√2)=+((2/p^2 )+((4−2(√2))/p^3 )+(2/p^6 ))(√(p^4 +1))+p^2 +(4−2(√2))p+(3/p^2 )+((4−2(√2))/p^3 )+(2/p^6 )+6−4]2 ... p(p−1)^2 (p^7 −2(7−4(√2))p^6 +5(11−8(√2))p^5 −4(5−4(√2))p^4 +(63−40(√2))p^3 −2(23−16(√2))p^3 +(73−48(√2))p−8(2−(√2)))=0 we know p≠0∧p≠1 we′re looking for 0<p<1 (there are several possible circles, touching C_1 from “wrong sides”) ⇒ p≈.631658=t_2 ⇒ r_2 ≈.327488 of course we can go on like this but I guess if I calculate with an error of ±10^(−14) at least t_(14) will have an error of ±1 ...](https://www.tinkutara.com/question/Q79514.png)
$$\mathrm{one}\:\mathrm{possible}\:\mathrm{path},\:\mathrm{but}\:\mathrm{no}\:\mathrm{exact}\:\mathrm{solution} \\ $$$$\mathrm{center}\:\mathrm{of}\:{C}_{{n}} ={M}_{{n}} =\begin{pmatrix}{{t}_{{n}} +\frac{\mathrm{1}}{{t}_{{n}} ^{\mathrm{3}} }−\frac{\mathrm{1}}{{t}_{{n}} ^{\mathrm{3}} }\sqrt{{t}_{{n}} ^{\mathrm{4}} +\mathrm{1}}}\\{\frac{\mathrm{2}}{{t}_{{n}} }−\frac{\mathrm{1}}{{t}_{{n}} }\sqrt{{t}_{{n}} ^{\mathrm{4}} +\mathrm{1}}}\end{pmatrix} \\ $$$$\mathrm{radius}\:\mathrm{of}\:{C}_{{n}} ={r}_{{n}} ={t}_{{n}} +\frac{\mathrm{1}}{{t}_{{n}} ^{\mathrm{3}} }−\frac{\mathrm{1}}{{t}_{{n}} ^{\mathrm{3}} }\sqrt{{t}_{{n}} ^{\mathrm{4}} +\mathrm{1}} \\ $$$$\:\:\:\:\:\left[{t}_{\mathrm{1}} =\mathrm{1}\:\Rightarrow\:{M}_{\mathrm{1}} =\begin{pmatrix}{\mathrm{2}−\sqrt{\mathrm{2}}}\\{\mathrm{2}−\sqrt{\mathrm{2}}}\end{pmatrix}\:\wedge\:{r}_{\mathrm{1}} =\mathrm{2}−\sqrt{\mathrm{2}}\right] \\ $$$$\mid{C}_{{n}} {C}_{{n}+\mathrm{1}} \mid^{\mathrm{2}} =\left({r}_{{n}} +{r}_{{n}+\mathrm{1}} \right)^{\mathrm{2}} \\ $$$$\mathrm{starting}\:\mathrm{with}\:{n}=\mathrm{1} \\ $$$$\mathrm{let}\:{t}_{\mathrm{2}} ={p} \\ $$$$\left.\left(\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}{{p}}−\frac{\mathrm{6}}{{p}^{\mathrm{2}} }+\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}{{p}^{\mathrm{3}} }−\frac{\mathrm{2}}{{p}^{\mathrm{6}} }\right)\sqrt{{p}^{\mathrm{4}} +\mathrm{1}}+\mathrm{2}{p}^{\mathrm{2}} −\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right){p}−\frac{\mathrm{8}−\mathrm{4}\sqrt{\mathrm{2}}}{{p}}+\frac{\mathrm{8}}{{p}^{\mathrm{2}} }−\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}{{p}^{\mathrm{3}} }+\frac{\mathrm{2}}{{p}^{\mathrm{6}} }+\mathrm{12}−\mathrm{8}\sqrt{\mathrm{2}}=+\left(\frac{\mathrm{2}}{{p}^{\mathrm{2}} }+\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}{{p}^{\mathrm{3}} }+\frac{\mathrm{2}}{{p}^{\mathrm{6}} }\right)\sqrt{{p}^{\mathrm{4}} +\mathrm{1}}+{p}^{\mathrm{2}} +\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right){p}+\frac{\mathrm{3}}{{p}^{\mathrm{2}} }+\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}{{p}^{\mathrm{3}} }+\frac{\mathrm{2}}{{p}^{\mathrm{6}} }+\mathrm{6}−\mathrm{4}\right]\mathrm{2} \\ $$$$… \\ $$$${p}\left({p}−\mathrm{1}\right)^{\mathrm{2}} \left({p}^{\mathrm{7}} −\mathrm{2}\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{2}}\right){p}^{\mathrm{6}} +\mathrm{5}\left(\mathrm{11}−\mathrm{8}\sqrt{\mathrm{2}}\right){p}^{\mathrm{5}} −\mathrm{4}\left(\mathrm{5}−\mathrm{4}\sqrt{\mathrm{2}}\right){p}^{\mathrm{4}} +\left(\mathrm{63}−\mathrm{40}\sqrt{\mathrm{2}}\right){p}^{\mathrm{3}} −\mathrm{2}\left(\mathrm{23}−\mathrm{16}\sqrt{\mathrm{2}}\right){p}^{\mathrm{3}} +\left(\mathrm{73}−\mathrm{48}\sqrt{\mathrm{2}}\right){p}−\mathrm{8}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\right)=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{know}\:{p}\neq\mathrm{0}\wedge{p}\neq\mathrm{1} \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{0}<{p}<\mathrm{1}\:\:\left(\mathrm{there}\:\mathrm{are}\:\mathrm{several}\right. \\ $$$$\:\:\:\:\:\mathrm{possible}\:\mathrm{circles},\:\mathrm{touching}\:{C}_{\mathrm{1}} \:\mathrm{from}\:“\mathrm{wrong} \\ $$$$\left.\:\:\:\:\:\mathrm{sides}''\right) \\ $$$$\Rightarrow\:{p}\approx.\mathrm{631658}={t}_{\mathrm{2}} \\ $$$$\Rightarrow\:{r}_{\mathrm{2}} \approx.\mathrm{327488} \\ $$$$\mathrm{of}\:\mathrm{course}\:\mathrm{we}\:\mathrm{can}\:\mathrm{go}\:\mathrm{on}\:\mathrm{like}\:\mathrm{this}\:\mathrm{but}\:\mathrm{I}\:\mathrm{guess} \\ $$$$\mathrm{if}\:\mathrm{I}\:\mathrm{calculate}\:\mathrm{with}\:\mathrm{an}\:\mathrm{error}\:\mathrm{of}\:\pm\mathrm{10}^{−\mathrm{14}} \:\mathrm{at}\:\mathrm{least} \\ $$$${t}_{\mathrm{14}} \:\mathrm{will}\:\mathrm{have}\:\mathrm{an}\:\mathrm{error}\:\mathrm{of}\:\pm\mathrm{1}\:… \\ $$
Answered by mr W last updated on 25/Jan/20
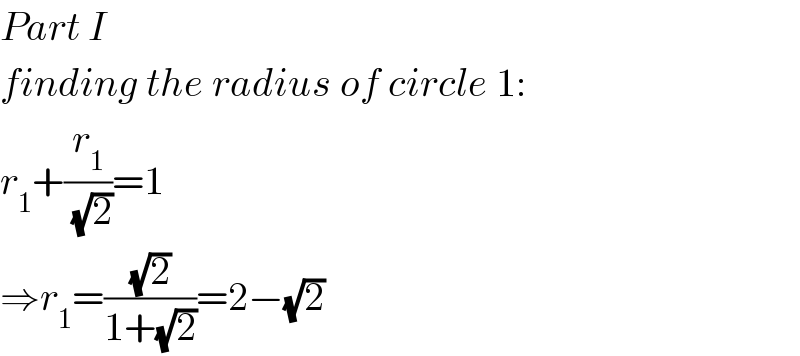
$${Part}\:{I} \\ $$$${finding}\:{the}\:{radius}\:{of}\:{circle}\:\mathrm{1}: \\ $$$${r}_{\mathrm{1}} +\frac{{r}_{\mathrm{1}} }{\:\sqrt{\mathrm{2}}}=\mathrm{1} \\ $$$$\Rightarrow{r}_{\mathrm{1}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}}=\mathrm{2}−\sqrt{\mathrm{2}} \\ $$
Commented by mr W last updated on 25/Jan/20

Commented by mr W last updated on 25/Jan/20

$${Part}\:{II}\:\left({just}\:{an}\:{attempt}…\right) \\ $$$${n}−{th}\:{circle}\:{with}\:{radius}\:{r}_{{n}} \:{and}\:{center} \\ $$$${at}\:{A}\left({r}_{{n}} ,{y}_{{A}} \right). \\ $$$$\left({x}−{r}_{{n}} \right)^{\mathrm{2}} +\left({y}−{y}_{{A}} \right)^{\mathrm{2}} ={r}_{{n}} ^{\mathrm{2}} \\ $$$${it}\:{touches}\:{the}\:{curve}\:{y}=\frac{\mathrm{1}}{{x}}\:{at}\:{C}\left({x}_{{C}} ,\frac{\mathrm{1}}{{x}_{{C}} }\right) \\ $$$$\left({x}_{{C}} −{r}_{{n}} \right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{x}_{{C}} }−{y}_{{A}} \right)^{\mathrm{2}} ={r}_{{n}} ^{\mathrm{2}} \\ $$$$\mathrm{tan}\:\theta=\frac{\frac{\mathrm{1}}{{x}_{{C}} }−{y}_{{A}} }{{x}_{{C}} −{r}_{{n}} }=−\frac{\mathrm{1}}{{y}'}={x}_{{C}} ^{\mathrm{2}} \\ $$$$\Rightarrow{y}_{{A}} =\frac{\mathrm{1}}{{x}_{{C}} }−{x}_{{C}} ^{\mathrm{2}} \left({x}_{{C}} −{r}_{{n}} \right) \\ $$$$\Rightarrow\left({x}_{{C}} −{r}_{{n}} \right)^{\mathrm{2}} \left(\mathrm{1}+{x}_{{C}} ^{\mathrm{4}} \right)={r}_{{n}} ^{\mathrm{2}} \\ $$$$\Rightarrow{x}_{{C}} ^{\mathrm{5}} −\mathrm{2}{r}_{{n}} {x}_{{C}} ^{\mathrm{4}} +{r}_{{n}} ^{\mathrm{2}} {x}_{{C}} ^{\mathrm{3}} +{x}_{{C}} −\mathrm{2}{r}_{{n}} =\mathrm{0} \\ $$$$……\:{it}'{s}\:{unsolvable}\:{for}\:{me}\:{upon}\:{here} \\ $$
Commented by behi83417@gmail.com last updated on 25/Jan/20

$$\mathrm{wow}!\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{attemping}\:\mathrm{dear}\:\mathrm{masters}: \\ $$$$\mathrm{sir}:\mathrm{MJS}\:\mathrm{and}\:\mathrm{sir}:\:\mathrm{mrW}. \\ $$
Commented by behi83417@gmail.com last updated on 25/Jan/20
![x_c ^3 .r_n ^2 −2(1+x_c ^4 )r_n +x_c ^5 +x_c =0 r_n =((1+x_c ^4 ±(√((1+x_c ^4 )^2 −x_c ^3 (x_c ^5 +x_c ))))/x_c ^3 ) ⇒r_n = { (((1+x_c ^4 +(√(1+x_c ^4 )))/x_c ^3 )),(((1+x_c ^4 −(√(1+x_c ^4 )))/x_c ^3 )) :} ⇒^(x_c =x) (∂r_n /∂x_c )=(((4x^3 +((2x^3 )/( (√(1+x^4 )))))x^3 −3x^2 (1+x^4 +(√(1+x^4 ))))/x^6 )=0 ⇒x^2 [4x^4 (√(1+x^4 ))+2x^3 )−3(1+x^4 +(1+x^4 )(√(1+x^4 )))]=0 ⇒ { (,(x=0 [not ok])),(,(4x^4 (√(1+x^4 ))+2x^3 −3−3x^4 −3(√(1+x^4 ))−3x^4 (√(1+x^4 ))=0)) :} ⇒(√(1+x^4 ))(x^4 −3)=3x^4 −2x^3 +3 ⇒(1+x^4 )(x^8 −6x^4 +9)=9x^8 +4x^6 +9−12x^7 +18x^4 −12x^3 ⇒x^(12) −5x^8 +3x^4 +9=9x^8 −12x^7 +4x^6 +18x^4 −12x^3 ⇒x^(12) −14x^8 +12x^7 −4x^6 −15x^4 +12x^3 =0 ⇒ { ((x^3 =0[not ok])),((x^9 −14x^5 +12x^4 −4x^3 −15x+12=0)) :} ⇒x=−2.51 ,0.733 ,1.747 ⇒r_n =((1+1.747^4 +(√(1+1.747^4 )))/(1.747^3 ))=2.537(×) ⇒r_n =((1+.733^4 +(√(1+.733^4 )))/(0.733^3 ))=6.155 (×) ⇒r_n =((1+(−2.51)^4 +(√(1+(−2.51)^4 )))/((−2.51)^3 ))=−2.97(×)](https://www.tinkutara.com/question/Q79483.png)
$$\mathrm{x}_{\mathrm{c}} ^{\mathrm{3}} .\mathrm{r}_{\mathrm{n}} ^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+\mathrm{x}_{\mathrm{c}} ^{\mathrm{4}} \right)\mathrm{r}_{\mathrm{n}} +\mathrm{x}_{\mathrm{c}} ^{\mathrm{5}} +\mathrm{x}_{\mathrm{c}} =\mathrm{0} \\ $$$$\mathrm{r}_{\mathrm{n}} =\frac{\mathrm{1}+\mathrm{x}_{\mathrm{c}} ^{\mathrm{4}} \pm\sqrt{\left(\mathrm{1}+\mathrm{x}_{\mathrm{c}} ^{\mathrm{4}} \right)^{\mathrm{2}} −\mathrm{x}_{\mathrm{c}} ^{\mathrm{3}} \left(\mathrm{x}_{\mathrm{c}} ^{\mathrm{5}} +\mathrm{x}_{\mathrm{c}} \right)}}{\mathrm{x}_{\mathrm{c}} ^{\mathrm{3}} } \\ $$$$\Rightarrow\mathrm{r}_{\mathrm{n}} =\begin{cases}{\frac{\mathrm{1}+\mathrm{x}_{\mathrm{c}} ^{\mathrm{4}} +\sqrt{\mathrm{1}+\mathrm{x}_{\mathrm{c}} ^{\mathrm{4}} }}{\mathrm{x}_{\mathrm{c}} ^{\mathrm{3}} }}\\{\frac{\mathrm{1}+\mathrm{x}_{\mathrm{c}} ^{\mathrm{4}} −\sqrt{\mathrm{1}+\mathrm{x}_{\mathrm{c}} ^{\mathrm{4}} }}{\mathrm{x}_{\mathrm{c}} ^{\mathrm{3}} }}\end{cases} \\ $$$$\overset{\mathrm{x}_{\mathrm{c}} =\mathrm{x}} {\Rightarrow}\:\frac{\partial\mathrm{r}_{\mathrm{n}} }{\partial\mathrm{x}_{\mathrm{c}} }=\frac{\left(\mathrm{4x}^{\mathrm{3}} +\frac{\mathrm{2x}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}\right)\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} +\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\right)}{\mathrm{x}^{\mathrm{6}} }=\mathrm{0} \\ $$$$\left.\Rightarrow\mathrm{x}^{\mathrm{2}} \left[\mathrm{4x}^{\mathrm{4}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }+\mathrm{2x}^{\mathrm{3}} \right)−\mathrm{3}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} +\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\right)\right]=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{}&{\mathrm{x}=\mathrm{0}\:\:\left[\mathrm{not}\:\mathrm{ok}\right]}\\{}&{\mathrm{4x}^{\mathrm{4}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }+\mathrm{2x}^{\mathrm{3}} −\mathrm{3}−\mathrm{3x}^{\mathrm{4}} −\mathrm{3}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }−\mathrm{3x}^{\mathrm{4}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\left(\mathrm{x}^{\mathrm{4}} −\mathrm{3}\right)=\mathrm{3x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{3}} +\mathrm{3} \\ $$$$\Rightarrow\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)\left(\mathrm{x}^{\mathrm{8}} −\mathrm{6x}^{\mathrm{4}} +\mathrm{9}\right)=\mathrm{9x}^{\mathrm{8}} +\mathrm{4x}^{\mathrm{6}} +\mathrm{9}−\mathrm{12x}^{\mathrm{7}} +\mathrm{18x}^{\mathrm{4}} −\mathrm{12x}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{12}} −\mathrm{5x}^{\mathrm{8}} +\mathrm{3x}^{\mathrm{4}} +\mathrm{9}=\mathrm{9x}^{\mathrm{8}} −\mathrm{12x}^{\mathrm{7}} +\mathrm{4x}^{\mathrm{6}} +\mathrm{18x}^{\mathrm{4}} −\mathrm{12x}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{12}} −\mathrm{14x}^{\mathrm{8}} +\mathrm{12x}^{\mathrm{7}} −\mathrm{4x}^{\mathrm{6}} −\mathrm{15x}^{\mathrm{4}} +\mathrm{12x}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{\mathrm{x}^{\mathrm{3}} =\mathrm{0}\left[\mathrm{not}\:\mathrm{ok}\right]}\\{\mathrm{x}^{\mathrm{9}} −\mathrm{14x}^{\mathrm{5}} +\mathrm{12x}^{\mathrm{4}} −\mathrm{4x}^{\mathrm{3}} −\mathrm{15x}+\mathrm{12}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\mathrm{x}=−\mathrm{2}.\mathrm{51}\:,\mathrm{0}.\mathrm{733}\:,\mathrm{1}.\mathrm{747} \\ $$$$\Rightarrow\mathrm{r}_{\mathrm{n}} =\frac{\mathrm{1}+\mathrm{1}.\mathrm{747}^{\mathrm{4}} +\sqrt{\mathrm{1}+\mathrm{1}.\mathrm{747}^{\mathrm{4}} }}{\mathrm{1}.\mathrm{747}^{\mathrm{3}} }=\mathrm{2}.\mathrm{537}\left(×\right) \\ $$$$\Rightarrow\mathrm{r}_{\mathrm{n}} =\frac{\mathrm{1}+.\mathrm{733}^{\mathrm{4}} +\sqrt{\mathrm{1}+.\mathrm{733}^{\mathrm{4}} }}{\mathrm{0}.\mathrm{733}^{\mathrm{3}} }=\mathrm{6}.\mathrm{155}\:\left(×\right) \\ $$$$\Rightarrow\mathrm{r}_{\mathrm{n}} =\frac{\mathrm{1}+\left(−\mathrm{2}.\mathrm{51}\right)^{\mathrm{4}} +\sqrt{\mathrm{1}+\left(−\mathrm{2}.\mathrm{51}\right)^{\mathrm{4}} }}{\left(−\mathrm{2}.\mathrm{51}\right)^{\mathrm{3}} }=−\mathrm{2}.\mathrm{97}\left(×\right) \\ $$
