Menu Close

Question-79520

Tinku Tara 0 Comments
Pin




Question Number 79520 by TawaTawa last updated on 25/Jan/20
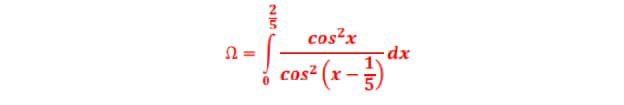
Commented by mathmax by abdo last updated on 26/Jan/20
Ω =∫_0 ^(2/5) ((cos^2 x)/(cos^2 (x−(1/5))))dx =∫_0 ^(2/5) ((1+cos(2x))/(1+cos(2x−(2/5))))dx =_(2x=t) (1/2) ∫_0 ^(4/5) ((1+cost)/(1+cos(t−(2/5))))dt =_(t−(2/5)=u) (1/2)∫_(−(2/5)) ^(2/5) ((1+cos(u+(2/5)))/(1+cosu))du ⇒2Ω =∫_(−(2/5)) ^(2/5) ((1+cos((2/5))cosu −sin((2/5))sinu)/(1+cosu)) du =∫_(−(2/5)) ^(2/5) (du/(1+cosu)) +cos((2/5))∫_(−(2/5)) ^(2/5) ((cosu)/(1+cosu))du−sin((2/5))∫_(−(2/5)) ^(2/5) ((sinu)/(1+codu))du(→0) Ω= ∫_0 ^(2/5) (du/(1+cosu)) +cos((2/5))∫_0 ^(2/(5 )) ((cosu)/(1+cosu))du ∫_0 ^(2/(5 )) (du/(1+cosu))du =_(tan((u/2))=z) ∫_0 ^(tan((1/5))) (1/(1+((1−z^2 )/(1+z^2 ))))×((2dz)/(1+z^2 )) =2 ∫_0 ^(tan((1/5))) (dz/(1+z^2 +1−z^2 )) =tan((1/5)) ∫_0 ^(2/5) ((cosu)/(1+cosu))du =∫_0 ^(2/5) ((1+cosu−1)/(1+cosu))du =(2/5) −tan((1/5)) ⇒ Ω =tan((1/5))+cos((2/5))((2/5) −tan((1/5)))
$$\Omega\:=\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{{cos}^{\mathrm{2}} {x}}{{cos}^{\mathrm{2}} \left({x}−\frac{\mathrm{1}}{\mathrm{5}}\right)}{dx}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{cos}\left(\mathrm{2}{x}−\frac{\mathrm{2}}{\mathrm{5}}\right)}{dx} \\ $$$$=_{\mathrm{2}{x}={t}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{4}}{\mathrm{5}}} \:\frac{\mathrm{1}+{cost}}{\mathrm{1}+{cos}\left({t}−\frac{\mathrm{2}}{\mathrm{5}}\right)}{dt}\:=_{{t}−\frac{\mathrm{2}}{\mathrm{5}}={u}} \:\frac{\mathrm{1}}{\mathrm{2}}\int_{−\frac{\mathrm{2}}{\mathrm{5}}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{\mathrm{1}+{cos}\left({u}+\frac{\mathrm{2}}{\mathrm{5}}\right)}{\mathrm{1}+{cosu}}{du} \\ $$$$\Rightarrow\mathrm{2}\Omega\:=\int_{−\frac{\mathrm{2}}{\mathrm{5}}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{\mathrm{1}+{cos}\left(\frac{\mathrm{2}}{\mathrm{5}}\right){cosu}\:−{sin}\left(\frac{\mathrm{2}}{\mathrm{5}}\right){sinu}}{\mathrm{1}+{cosu}}\:{du} \\ $$$$=\int_{−\frac{\mathrm{2}}{\mathrm{5}}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{{du}}{\mathrm{1}+{cosu}}\:+{cos}\left(\frac{\mathrm{2}}{\mathrm{5}}\right)\int_{−\frac{\mathrm{2}}{\mathrm{5}}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{{cosu}}{\mathrm{1}+{cosu}}{du}−{sin}\left(\frac{\mathrm{2}}{\mathrm{5}}\right)\int_{−\frac{\mathrm{2}}{\mathrm{5}}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{{sinu}}{\mathrm{1}+{codu}}{du}\left(\rightarrow\mathrm{0}\right) \\ $$$$\Omega=\:\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{{du}}{\mathrm{1}+{cosu}}\:\:+{cos}\left(\frac{\mathrm{2}}{\mathrm{5}}\right)\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\mathrm{5}\:}} \:\frac{{cosu}}{\mathrm{1}+{cosu}}{du} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\mathrm{5}\:}} \:\frac{{du}}{\mathrm{1}+{cosu}}{du}\:=_{{tan}\left(\frac{{u}}{\mathrm{2}}\right)={z}} \:\:\:\int_{\mathrm{0}} ^{{tan}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)} \:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}−{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} }}×\frac{\mathrm{2}{dz}}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{{tan}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)} \:\frac{{dz}}{\mathrm{1}+{z}^{\mathrm{2}} \:+\mathrm{1}−{z}^{\mathrm{2}} }\:={tan}\left(\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{{cosu}}{\mathrm{1}+{cosu}}{du}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{2}}{\mathrm{5}}} \:\frac{\mathrm{1}+{cosu}−\mathrm{1}}{\mathrm{1}+{cosu}}{du}\:=\frac{\mathrm{2}}{\mathrm{5}}\:−{tan}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)\:\Rightarrow \\ $$$$\Omega\:={tan}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)+{cos}\left(\frac{\mathrm{2}}{\mathrm{5}}\right)\left(\frac{\mathrm{2}}{\mathrm{5}}\:−{tan}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)\right) \\ $$
Commented by TawaTawa last updated on 26/Jan/20
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 25/Jan/20
∫((cos^2 x)/(cos^2 (x−(1/5))))dx= [t=x−(1/5) → dx=dt] ∫((cos^2 (t+(1/5)))/(cos^2 t))dt= =((1+cos (2/5))/2)∫dt−sin (2/5)∫tan t dt+((1−cos (2/5))/2)∫tan^2 t dt= and these are easy to solve
$$\int\frac{\mathrm{cos}^{\mathrm{2}} \:{x}}{\mathrm{cos}^{\mathrm{2}} \:\left({x}−\frac{\mathrm{1}}{\mathrm{5}}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}−\frac{\mathrm{1}}{\mathrm{5}}\:\rightarrow\:{dx}={dt}\right] \\ $$$$\int\frac{\mathrm{cos}^{\mathrm{2}} \:\left({t}+\frac{\mathrm{1}}{\mathrm{5}}\right)}{\mathrm{cos}^{\mathrm{2}} \:{t}}{dt}= \\ $$$$=\frac{\mathrm{1}+\mathrm{cos}\:\frac{\mathrm{2}}{\mathrm{5}}}{\mathrm{2}}\int{dt}−\mathrm{sin}\:\frac{\mathrm{2}}{\mathrm{5}}\int\mathrm{tan}\:{t}\:{dt}+\frac{\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{2}}{\mathrm{5}}}{\mathrm{2}}\int\mathrm{tan}^{\mathrm{2}} \:{t}\:{dt}= \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *