Menu Close

Question-79538

Tinku Tara 0 Comments
Pin




Question Number 79538 by Pratah last updated on 26/Jan/20
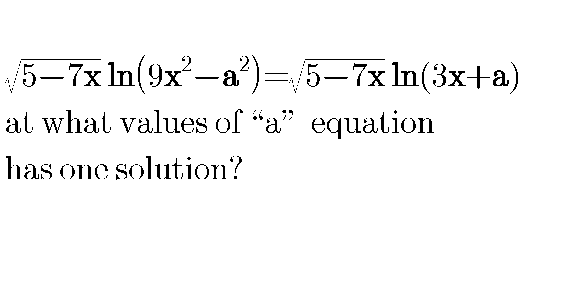
Commented by john santu last updated on 26/Jan/20
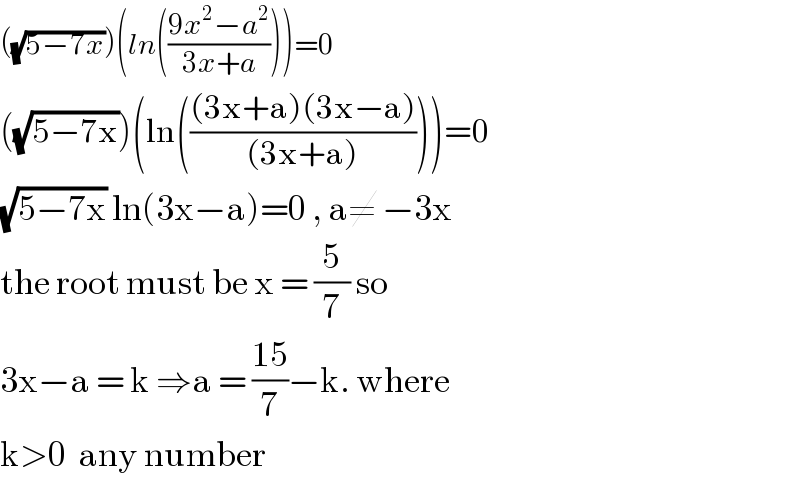
((√(5−7x)))(ln(((9x^2 −a^2 )/(3x+a))))=0 ((√(5−7x)))(ln((((3x+a)(3x−a))/((3x+a)))))=0 (√(5−7x)) ln(3x−a)=0 , a≠ −3x the root must be x = (5/7) so 3x−a = k ⇒a = ((15)/7)−k. where k>0 any number
$$\left(\sqrt{\mathrm{5}−\mathrm{7}{x}}\right)\left({ln}\left(\frac{\mathrm{9}{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{3}{x}+{a}}\right)\right)=\mathrm{0} \\ $$$$\left(\sqrt{\mathrm{5}−\mathrm{7x}}\right)\left(\mathrm{ln}\left(\frac{\left(\mathrm{3x}+\mathrm{a}\right)\left(\mathrm{3x}−\mathrm{a}\right)}{\left(\mathrm{3x}+\mathrm{a}\right)}\right)\right)=\mathrm{0} \\ $$$$\sqrt{\mathrm{5}−\mathrm{7x}}\:\mathrm{ln}\left(\mathrm{3x}−\mathrm{a}\right)=\mathrm{0}\:,\:\mathrm{a}\neq\:−\mathrm{3x} \\ $$$$\mathrm{the}\:\mathrm{root}\:\mathrm{must}\:\mathrm{be}\:\mathrm{x}\:=\:\frac{\mathrm{5}}{\mathrm{7}}\:\mathrm{so} \\ $$$$\mathrm{3x}−\mathrm{a}\:=\:\mathrm{k}\:\Rightarrow\mathrm{a}\:=\:\frac{\mathrm{15}}{\mathrm{7}}−\mathrm{k}.\:\mathrm{where}\: \\ $$$$\mathrm{k}>\mathrm{0}\:\:\mathrm{any}\:\mathrm{number} \\ $$
Commented by Pratah last updated on 26/Jan/20
thanks
$$\mathrm{thanks} \\ $$
Commented by john santu last updated on 26/Jan/20
this answer right?
$${this}\:{answer}\:{right}? \\ $$
Commented by john santu last updated on 26/Jan/20
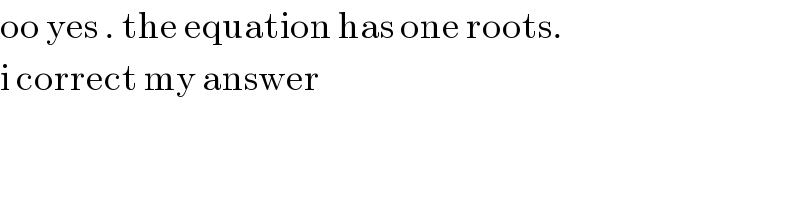
oo yes . the equation has one roots. i correct my answer
$$\mathrm{oo}\:\mathrm{yes}\:.\:\mathrm{the}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{one}\:\mathrm{roots}.\: \\ $$$$\mathrm{i}\:\mathrm{correct}\:\mathrm{my}\:\mathrm{answer} \\ $$
Commented by john santu last updated on 26/Jan/20
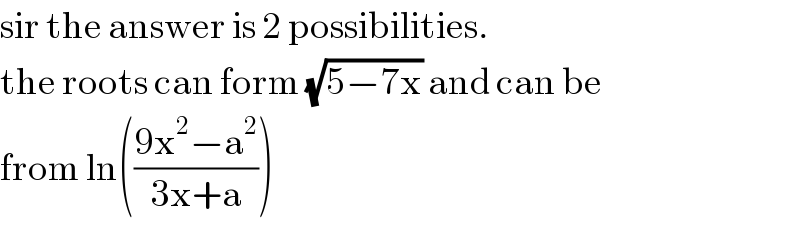
sir the answer is 2 possibilities. the roots can form (√(5−7x)) and can be from ln(((9x^2 −a^2 )/(3x+a)))
$$\mathrm{sir}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{2}\:\mathrm{possibilities}.\: \\ $$$$\mathrm{the}\:\mathrm{roots}\:\mathrm{can}\:\mathrm{form}\:\sqrt{\mathrm{5}−\mathrm{7x}}\:\mathrm{and}\:\mathrm{can}\:\mathrm{be}\: \\ $$$$\mathrm{from}\:\mathrm{ln}\left(\frac{\mathrm{9x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }{\mathrm{3x}+\mathrm{a}}\right) \\ $$
Commented by john santu last updated on 26/Jan/20
when we take the root out of shape (√(5−7x)) , so must be a≠ (8/7) ∧a≠−((15)/7)
$$\mathrm{when}\:\mathrm{we}\:\mathrm{take}\:\mathrm{the}\:\mathrm{root}\:\mathrm{out}\: \\ $$$$\mathrm{of}\:\mathrm{shape}\:\sqrt{\mathrm{5}−\mathrm{7x}}\:,\:\mathrm{so}\:\mathrm{must}\:\mathrm{be}\: \\ $$$$\mathrm{a}\neq\:\frac{\mathrm{8}}{\mathrm{7}}\:\wedge\mathrm{a}\neq−\frac{\mathrm{15}}{\mathrm{7}} \\ $$
Commented by jagoll last updated on 26/Jan/20
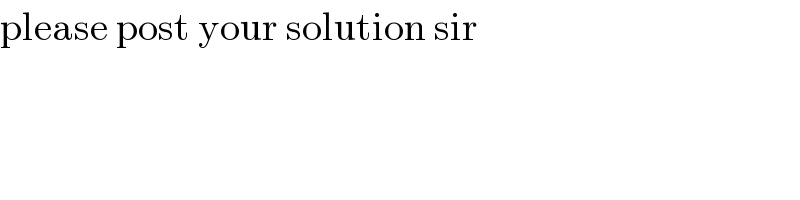
please post your solution sir
$$\mathrm{please}\:\mathrm{post}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 26/Jan/20
to jagoll sir: are you talking to Pratah sir? then you can directly talk to a wall. a wall may give yoy an echo back, but he not.
$${to}\:{jagoll}\:{sir}: \\ $$$${are}\:{you}\:{talking}\:{to}\:{Pratah}\:{sir}?\:{then} \\ $$$${you}\:{can}\:{directly}\:{talk}\:{to}\:{a}\:{wall}.\:{a}\:{wall} \\ $$$${may}\:{give}\:{yoy}\:{an}\:{echo}\:{back},\:{but}\:{he}\:{not}. \\ $$
Commented by jagoll last updated on 26/Jan/20
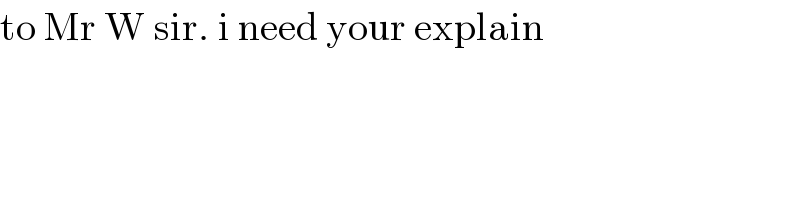
to Mr W sir. i need your explain
$$\mathrm{to}\:\mathrm{Mr}\:\mathrm{W}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{need}\:\mathrm{your}\:\mathrm{explain} \\ $$
Commented by jagoll last updated on 26/Jan/20
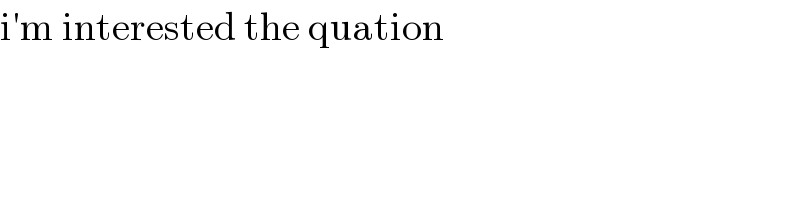
i′m interested the quation
$$\mathrm{i}'\mathrm{m}\:\mathrm{interested}\:\mathrm{the}\:\mathrm{quation} \\ $$
Commented by john santu last updated on 26/Jan/20
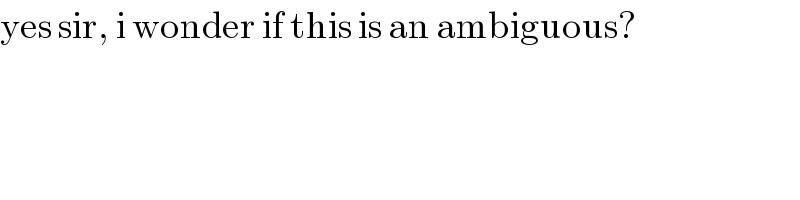
yes sir, i wonder if this is an ambiguous?
$$\mathrm{yes}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{wonder}\:\mathrm{if}\:\mathrm{this}\:\mathrm{is}\:\mathrm{an}\:\mathrm{ambiguous}? \\ $$
Commented by john santu last updated on 26/Jan/20
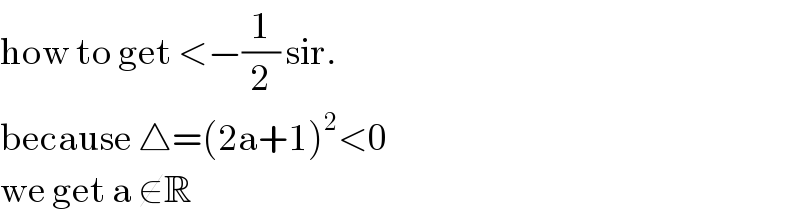
how to get <−(1/2) sir. because △=(2a+1)^2 <0 we get a ∉R
$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:<−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sir}.\:\: \\ $$$$\mathrm{because}\:\bigtriangleup=\left(\mathrm{2a}+\mathrm{1}\right)^{\mathrm{2}} <\mathrm{0}\: \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\notin\mathbb{R} \\ $$
Commented by john santu last updated on 26/Jan/20
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 26/Jan/20
the original equation can be formed to (√(5−7x)){ln (9x^2 −a^2 )−ln (3x+a)}=0 without “loss”. such that the equation makes sense, 5−7x≥0 ⇒x≤(5/7) 3x+a>0 9x^2 −a^2 >0 ⇒(3x−a)(3x+a)>0 ⇒3x−a>0 we see the original eqn. has the root x=(5/7), when (3×(5/7))^2 >a^2 ⇒−((15)/7)<a<((15)/7) and 3×(5/7)>−a ⇒a>−((15)/7) that means if −((15)/7)<a<((15)/7) the eqn. has always the root x=(5/7). such that the eqn. has only this root, the equation ln (9x^2 −a^2 )−ln (3x+a)=0 should have no root or only the root (5/7). ln (9x^2 −a^2 )−ln (3x+a)=0 ⇒ln (3x−a)=0 ⇒3x−a=1 it has always a root x=((a+1)/3) so this root must be (5/7). ((a+1)/3)=(5/7) ⇒a=(8/7) which lies in (−((15)/7),((15)/7)) therefore the answer is when a=(8/7), the original equation has “one” root.
$${the}\:{original}\:{equation}\:{can}\:{be}\:{formed}\:{to} \\ $$$$\sqrt{\mathrm{5}−\mathrm{7}{x}}\left\{\mathrm{ln}\:\left(\mathrm{9}{x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)−\mathrm{ln}\:\left(\mathrm{3}{x}+{a}\right)\right\}=\mathrm{0} \\ $$$${without}\:“{loss}''. \\ $$$${such}\:{that}\:{the}\:{equation}\:{makes}\:{sense}, \\ $$$$\mathrm{5}−\mathrm{7}{x}\geqslant\mathrm{0}\:\Rightarrow{x}\leqslant\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\mathrm{3}{x}+{a}>\mathrm{0}\: \\ $$$$\mathrm{9}{x}^{\mathrm{2}} −{a}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow\left(\mathrm{3}{x}−{a}\right)\left(\mathrm{3}{x}+{a}\right)>\mathrm{0}\:\Rightarrow\mathrm{3}{x}−{a}>\mathrm{0} \\ $$$$ \\ $$$${we}\:{see}\:{the}\:{original}\:{eqn}.\:{has}\:{the}\:{root} \\ $$$${x}=\frac{\mathrm{5}}{\mathrm{7}},\:{when}\:\left(\mathrm{3}×\frac{\mathrm{5}}{\mathrm{7}}\right)^{\mathrm{2}} >{a}^{\mathrm{2}} \:\Rightarrow−\frac{\mathrm{15}}{\mathrm{7}}<{a}<\frac{\mathrm{15}}{\mathrm{7}} \\ $$$${and}\:\mathrm{3}×\frac{\mathrm{5}}{\mathrm{7}}>−{a}\:\Rightarrow{a}>−\frac{\mathrm{15}}{\mathrm{7}} \\ $$$${that}\:{means}\:{if}\:−\frac{\mathrm{15}}{\mathrm{7}}<{a}<\frac{\mathrm{15}}{\mathrm{7}}\:{the}\:{eqn}. \\ $$$${has}\:{always}\:{the}\:{root}\:{x}=\frac{\mathrm{5}}{\mathrm{7}}. \\ $$$${such}\:{that}\:{the}\:{eqn}.\:{has}\:{only}\:{this}\:{root}, \\ $$$${the}\:{equation} \\ $$$$\mathrm{ln}\:\left(\mathrm{9}{x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)−\mathrm{ln}\:\left(\mathrm{3}{x}+{a}\right)=\mathrm{0} \\ $$$${should}\:{have}\:{no}\:{root}\:{or}\:{only}\:{the}\:{root}\:\frac{\mathrm{5}}{\mathrm{7}}. \\ $$$$\mathrm{ln}\:\left(\mathrm{9}{x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)−\mathrm{ln}\:\left(\mathrm{3}{x}+{a}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{ln}\:\left(\mathrm{3}{x}−{a}\right)=\mathrm{0}\:\Rightarrow\mathrm{3}{x}−{a}=\mathrm{1} \\ $$$${it}\:{has}\:{always}\:{a}\:{root}\:{x}=\frac{{a}+\mathrm{1}}{\mathrm{3}} \\ $$$${so}\:{this}\:{root}\:{must}\:{be}\:\frac{\mathrm{5}}{\mathrm{7}}. \\ $$$$\frac{{a}+\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{8}}{\mathrm{7}}\:{which}\:{lies}\:{in}\:\left(−\frac{\mathrm{15}}{\mathrm{7}},\frac{\mathrm{15}}{\mathrm{7}}\right) \\ $$$$ \\ $$$${therefore}\:{the}\:{answer}\:{is} \\ $$$${when}\:{a}=\frac{\mathrm{8}}{\mathrm{7}},\:{the}\:{original}\:{equation} \\ $$$${has}\:“{one}''\:{root}. \\ $$
Commented by mr W last updated on 26/Jan/20
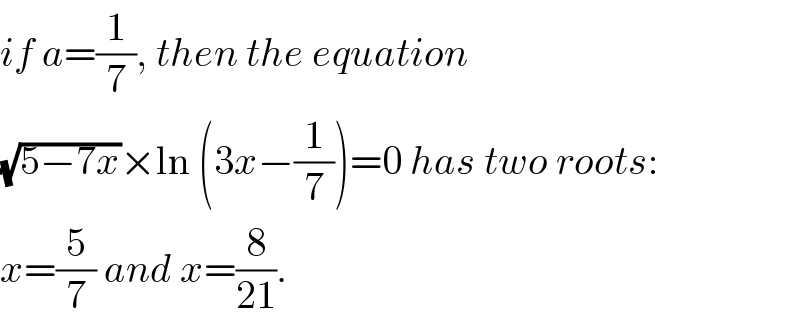
if a=(1/7), then the equation (√(5−7x))×ln (3x−(1/7))=0 has two roots: x=(5/7) and x=(8/(21)).
$${if}\:{a}=\frac{\mathrm{1}}{\mathrm{7}},\:{then}\:{the}\:{equation} \\ $$$$\sqrt{\mathrm{5}−\mathrm{7}{x}}×\mathrm{ln}\:\left(\mathrm{3}{x}−\frac{\mathrm{1}}{\mathrm{7}}\right)=\mathrm{0}\:{has}\:{two}\:{roots}: \\ $$$${x}=\frac{\mathrm{5}}{\mathrm{7}}\:{and}\:{x}=\frac{\mathrm{8}}{\mathrm{21}}. \\ $$
Commented by john santu last updated on 26/Jan/20
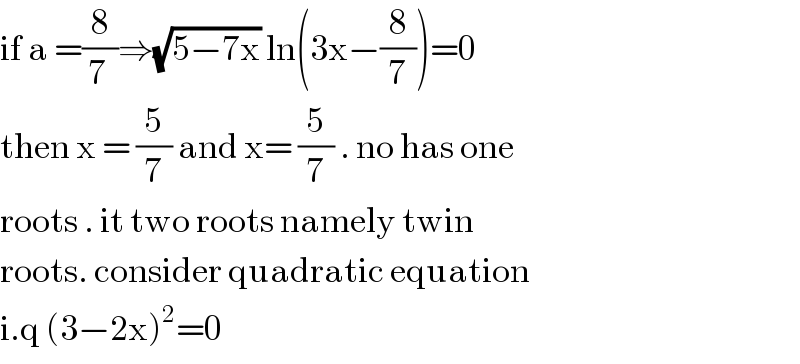
if a =(8/(7 ))⇒(√(5−7x)) ln(3x−(8/7))=0 then x = (5/7) and x= (5/7) . no has one roots . it two roots namely twin roots. consider quadratic equation i.q (3−2x)^2 =0
$$\mathrm{if}\:\mathrm{a}\:=\frac{\mathrm{8}}{\mathrm{7}\:}\Rightarrow\sqrt{\mathrm{5}−\mathrm{7x}}\:\mathrm{ln}\left(\mathrm{3x}−\frac{\mathrm{8}}{\mathrm{7}}\right)=\mathrm{0} \\ $$$$\mathrm{then}\:\mathrm{x}\:=\:\frac{\mathrm{5}}{\mathrm{7}}\:\mathrm{and}\:\mathrm{x}=\:\frac{\mathrm{5}}{\mathrm{7}}\:.\:\mathrm{no}\:\mathrm{has}\:\mathrm{one}\: \\ $$$$\mathrm{roots}\:.\:\mathrm{it}\:\mathrm{two}\:\mathrm{roots}\:\mathrm{namely}\:\mathrm{twin} \\ $$$$\mathrm{roots}.\:\mathrm{consider}\:\mathrm{quadratic}\:\mathrm{equation} \\ $$$$\mathrm{i}.\mathrm{q}\:\left(\mathrm{3}−\mathrm{2x}\right)^{\mathrm{2}} =\mathrm{0} \\ $$
Commented by john santu last updated on 26/Jan/20
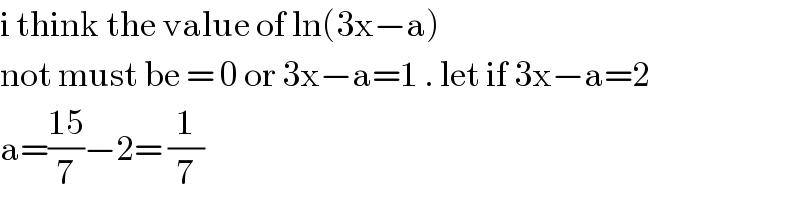
i think the value of ln(3x−a) not must be = 0 or 3x−a=1 . let if 3x−a=2 a=((15)/7)−2= (1/7)
$$\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{ln}\left(\mathrm{3x}−\mathrm{a}\right)\: \\ $$$$\mathrm{not}\:\mathrm{must}\:\mathrm{be}\:=\:\mathrm{0}\:\mathrm{or}\:\mathrm{3x}−\mathrm{a}=\mathrm{1}\:.\:\mathrm{let}\:\mathrm{if}\:\mathrm{3x}−\mathrm{a}=\mathrm{2} \\ $$$$\mathrm{a}=\frac{\mathrm{15}}{\mathrm{7}}−\mathrm{2}=\:\frac{\mathrm{1}}{\mathrm{7}} \\ $$
Commented by mr W last updated on 26/Jan/20
if there are n values of x such that f(x)=0, then we say the eqn. f(x)=0 has n roots. the eqnuation (√(5−7x)) ln(3x−(8/7))=0 has only “one” root, namely x=(5/7), no two! in case of a polynomial equation n−th order we say it has always n roots, but m roots of them can be the same, because the polynomial may have factors like (3−2x)^m . but in our case we don′t have to do with polynomial.
$${if}\:{there}\:{are}\:{n}\:{values}\:{of}\:{x}\:{such}\:{that} \\ $$$${f}\left({x}\right)=\mathrm{0},\:{then}\:{we}\:{say}\:{the}\:{eqn}.\:{f}\left({x}\right)=\mathrm{0} \\ $$$${has}\:{n}\:{roots}. \\ $$$${the}\:{eqnuation}\:\:\sqrt{\mathrm{5}−\mathrm{7x}}\:\mathrm{ln}\left(\mathrm{3x}−\frac{\mathrm{8}}{\mathrm{7}}\right)=\mathrm{0}\:{has} \\ $$$${only}\:“{one}''\:{root},\:{namely}\:{x}=\frac{\mathrm{5}}{\mathrm{7}},\:{no}\:{two}! \\ $$$${in}\:{case}\:{of}\:{a}\:{polynomial}\:{equation}\:{n}−{th} \\ $$$${order}\:{we}\:{say}\:{it}\:{has}\:{always}\:{n}\:{roots}, \\ $$$${but}\:{m}\:{roots}\:{of}\:{them}\:{can}\:{be}\:{the}\:{same}, \\ $$$${because}\:{the}\:{polynomial}\:{may}\:{have} \\ $$$${factors}\:{like}\:\left(\mathrm{3}−\mathrm{2}{x}\right)^{{m}} . \\ $$$${but}\:{in}\:{our}\:{case}\:{we}\:{don}'{t}\:{have}\:{to}\:{do}\:{with} \\ $$$${polynomial}. \\ $$
Commented by mr W last updated on 26/Jan/20
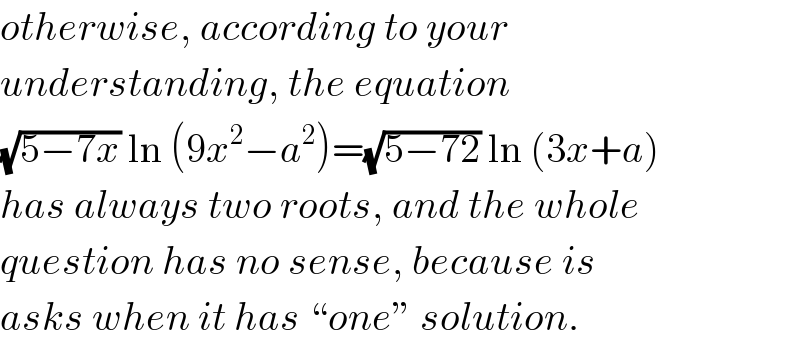
otherwise, according to your understanding, the equation (√(5−7x)) ln (9x^2 −a^2 )=(√(5−72)) ln (3x+a) has always two roots, and the whole question has no sense, because is asks when it has “one” solution.
$${otherwise},\:{according}\:{to}\:{your} \\ $$$${understanding},\:{the}\:{equation} \\ $$$$\sqrt{\mathrm{5}−\mathrm{7}{x}}\:\mathrm{ln}\:\left(\mathrm{9}{x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)=\sqrt{\mathrm{5}−\mathrm{72}}\:\mathrm{ln}\:\left(\mathrm{3}{x}+{a}\right) \\ $$$${has}\:{always}\:{two}\:{roots},\:{and}\:{the}\:{whole} \\ $$$${question}\:{has}\:{no}\:{sense},\:{because}\:{is} \\ $$$${asks}\:{when}\:{it}\:{has}\:“{one}''\:{solution}. \\ $$
Commented by john santu last updated on 26/Jan/20
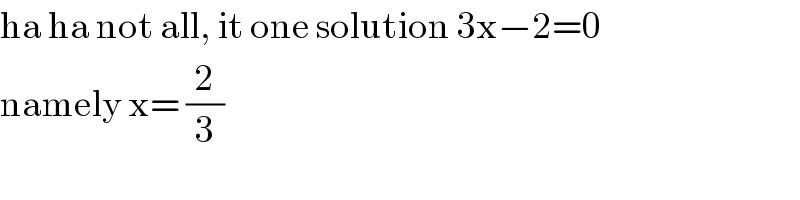
ha ha not all, it one solution 3x−2=0 namely x= (2/3)
$$\mathrm{ha}\:\mathrm{ha}\:\mathrm{not}\:\mathrm{all},\:\mathrm{it}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{3x}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{namely}\:\mathrm{x}=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 26/Jan/20
ok deal a = (8/7)
$$\mathrm{ok}\:\mathrm{deal}\:\mathrm{a}\:=\:\frac{\mathrm{8}}{\mathrm{7}} \\ $$
Commented by john santu last updated on 26/Jan/20
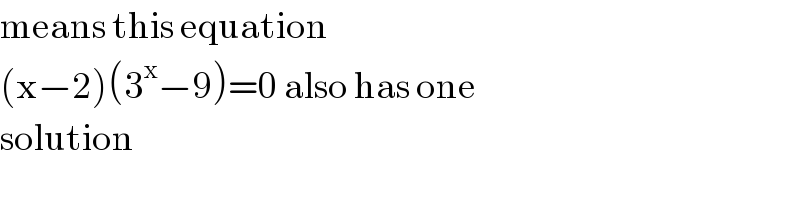
means this equation (x−2)(3^x −9)=0 also has one solution
$$\mathrm{means}\:\mathrm{this}\:\mathrm{equation}\: \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{3}^{\mathrm{x}} −\mathrm{9}\right)=\mathrm{0}\:\mathrm{also}\:\mathrm{has}\:\mathrm{one}\: \\ $$$$\mathrm{solution} \\ $$
Commented by mr W last updated on 26/Jan/20
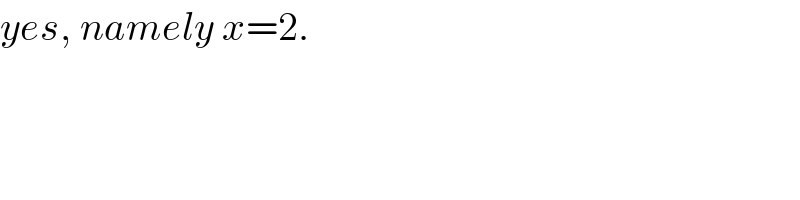
yes, namely x=2.
$${yes},\:{namely}\:{x}=\mathrm{2}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *