Question Number 79572 by ajfour last updated on 26/Jan/20
Commented by ajfour last updated on 26/Jan/20

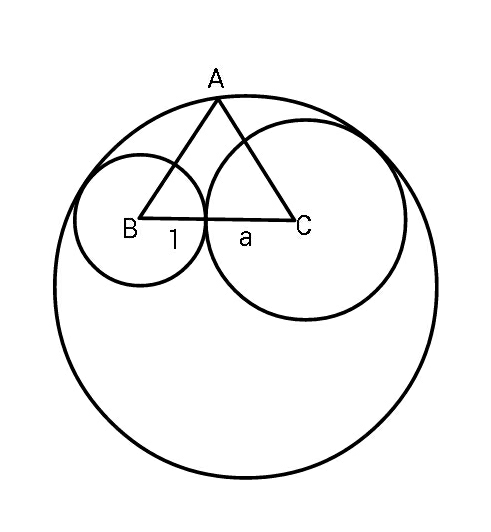
$$\bigtriangleup{ABC}\:{is}\:{equilateral}.\:{The}\:{smaller} \\ $$$${circles}\:{have}\:{radii}\:\mathrm{1}\:{and}\:{a}.\:{Find} \\ $$$${the}\:{circumcircle}\:{radius}. \\ $$
Answered by mr W last updated on 26/Jan/20
Commented by mr W last updated on 26/Jan/20

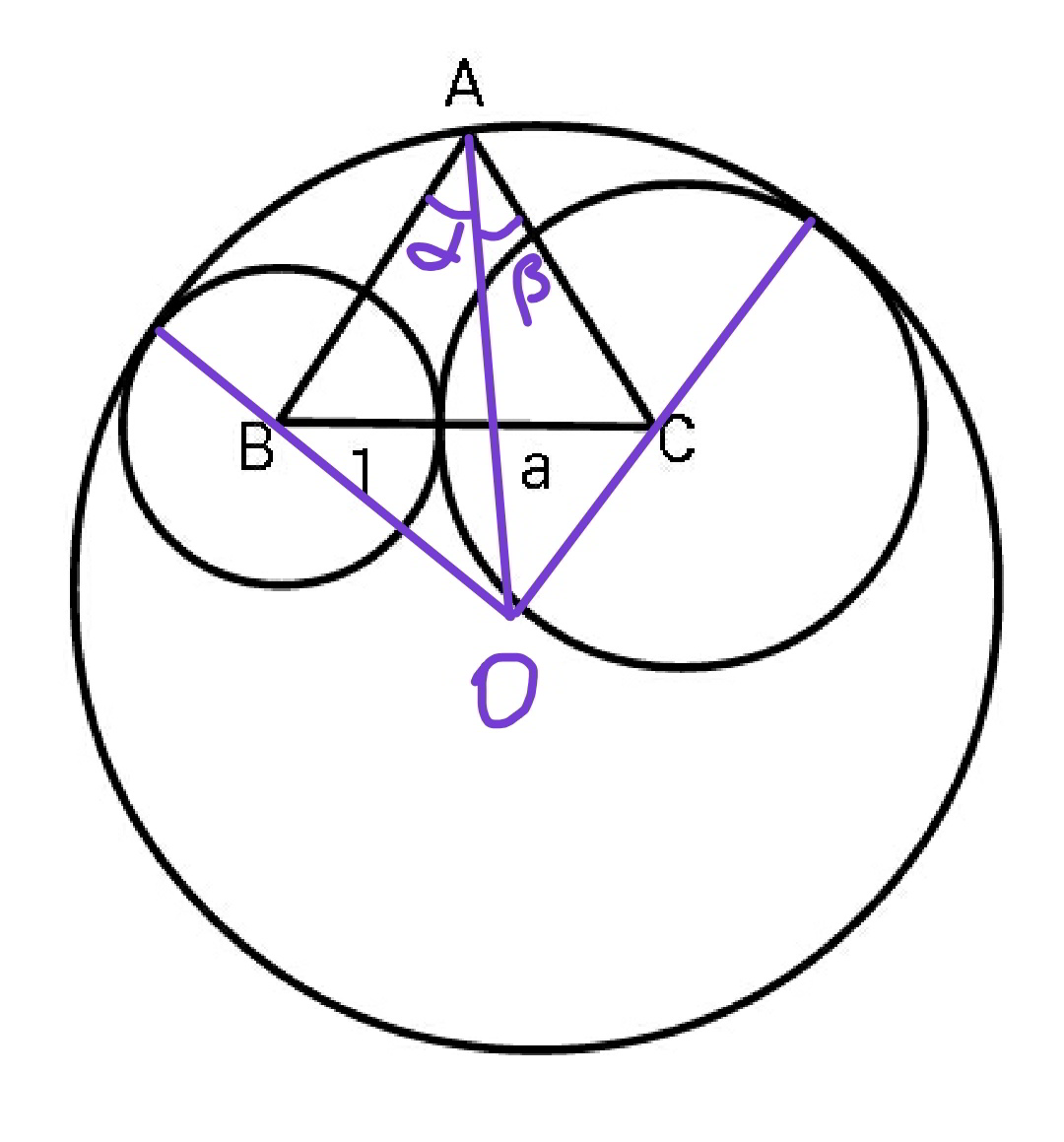
$${OA}={R} \\ $$$${OB}={R}−\mathrm{1} \\ $$$${OC}={R}−{a} \\ $$$${AB}={AC}=\mathrm{1}+{a} \\ $$$$\mathrm{cos}\:\alpha=\frac{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} −\left({R}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+{a}\right){R}}=\frac{{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{2}{R}}{\mathrm{2}{R}\left(\mathrm{1}+{a}\right)} \\ $$$$\mathrm{cos}\:\beta=\frac{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} −\left({R}−{a}\right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+{a}\right){R}}=\frac{\mathrm{1}+\mathrm{2}{a}+\mathrm{2}{Ra}}{\mathrm{2}{R}\left(\mathrm{1}+{a}\right)} \\ $$$$\alpha+\beta=\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{cos}\:\alpha=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}−\beta\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\beta+\sqrt{\mathrm{3}}\mathrm{sin}\:\beta\right) \\ $$$$\mathrm{2}×\frac{{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{2}{R}}{\mathrm{2}{R}\left(\mathrm{1}+{a}\right)}=\frac{\mathrm{1}+\mathrm{2}{a}+\mathrm{2}{Ra}}{\mathrm{2}{R}\left(\mathrm{1}+{a}\right)}+\frac{\sqrt{\mathrm{3}}\sqrt{\mathrm{4}{R}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{2}{a}\right)^{\mathrm{2}} −\left(\mathrm{1}+\mathrm{2}{a}\right)^{\mathrm{2}} −\mathrm{4}{a}\left(\mathrm{1}+\mathrm{2}{a}\right){R}}}{\mathrm{2}{R}\left(\mathrm{1}+{a}\right)} \\ $$$$\mathrm{2}\left(\mathrm{2}−{a}\right){R}+\left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{a}−\mathrm{1}\right)=\sqrt{\mathrm{3}}\sqrt{\mathrm{4}{R}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{2}{a}\right)^{\mathrm{2}} −\left(\mathrm{1}+\mathrm{2}{a}\right)^{\mathrm{2}} −\mathrm{4}{a}\left(\mathrm{1}+\mathrm{2}{a}\right){R}} \\ $$$$\mathrm{4}\left(\mathrm{2}−{a}\right)^{\mathrm{2}} {R}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{2}−{a}\right)\left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{a}−\mathrm{1}\right){R}+\left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{a}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{12}\left(\mathrm{1}+\mathrm{2}{a}\right)^{\mathrm{2}} {R}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{1}+\mathrm{2}{a}\right)^{\mathrm{2}} −\mathrm{12}{a}\left(\mathrm{1}+\mathrm{2}{a}\right){R} \\ $$$$\mathrm{2}\left(\mathrm{11}{a}^{\mathrm{2}} +\mathrm{16}{a}−\mathrm{1}\right){R}^{\mathrm{2}} +\left(\mathrm{2}{a}^{\mathrm{3}} −\mathrm{14}{a}^{\mathrm{2}} −\mathrm{11}{a}+\mathrm{2}\right){R}−\mathrm{2}\left({a}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{R}=\frac{\sqrt{\left(\mathrm{2}{a}^{\mathrm{3}} −\mathrm{14}{a}^{\mathrm{2}} −\mathrm{11}{a}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{16}\left(\mathrm{11}{a}^{\mathrm{2}} +\mathrm{16}{a}−\mathrm{1}\right)\left({a}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}\right)}−\left(\mathrm{2}{a}^{\mathrm{3}} −\mathrm{14}{a}^{\mathrm{2}} −\mathrm{11}{a}+\mathrm{2}\right)}{\mathrm{4}\left(\mathrm{11}{a}^{\mathrm{2}} +\mathrm{16}{a}−\mathrm{1}\right)} \\ $$
Commented by john santu last updated on 26/Jan/20

$$\mathrm{in}\:\mathrm{this}\:\mathrm{picture}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{see}\:\mathrm{the}\:\mathrm{letter}\:\mathrm{i} \\ $$
Commented by john santu last updated on 26/Jan/20
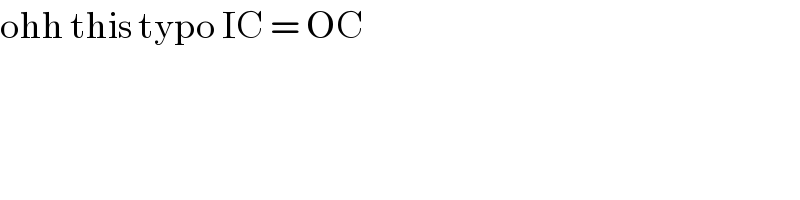
$$\mathrm{ohh}\:\mathrm{this}\:\mathrm{typo}\:\mathrm{IC}\:=\:\mathrm{OC} \\ $$
Commented by ajfour last updated on 26/Jan/20
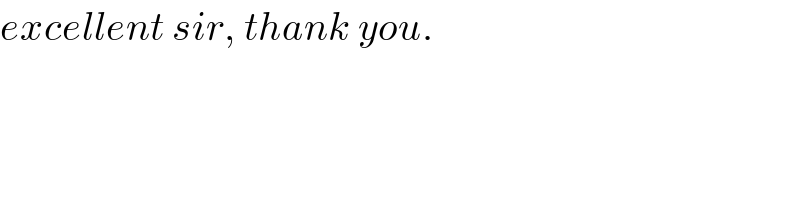
$${excellent}\:{sir},\:{thank}\:{you}. \\ $$
