Question Number 79609 by mr W last updated on 26/Jan/20

Commented by mr W last updated on 26/Jan/20

$${if}\:{the}\:{large}\:{square}\:{has}\:{the}\:{side}\:{length} \\ $$$$\mathrm{10},\:{find}\:{the}\:{radius}\:{r}\:{of}\:{the}\:{smallest} \\ $$$${circle}. \\ $$
Answered by ajfour last updated on 26/Jan/20
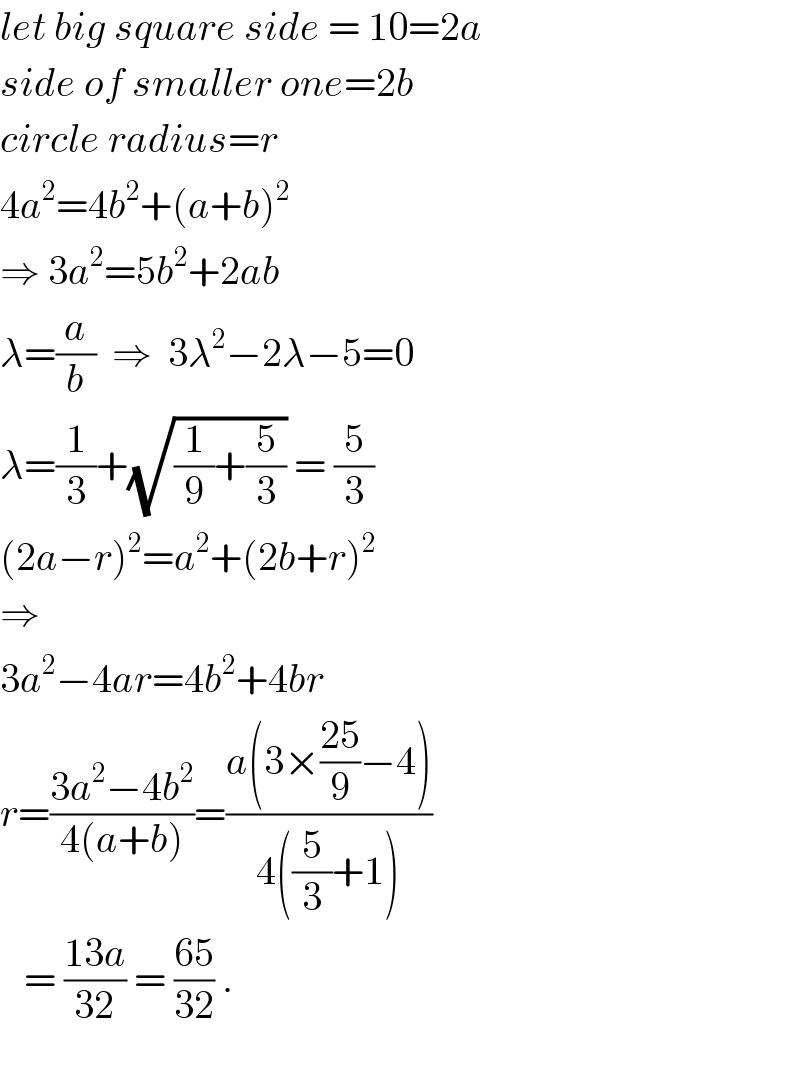
$${let}\:{big}\:{square}\:{side}\:=\:\mathrm{10}=\mathrm{2}{a} \\ $$$${side}\:{of}\:{smaller}\:{one}=\mathrm{2}{b} \\ $$$${circle}\:{radius}={r} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} =\mathrm{4}{b}^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{3}{a}^{\mathrm{2}} =\mathrm{5}{b}^{\mathrm{2}} +\mathrm{2}{ab} \\ $$$$\lambda=\frac{{a}}{{b}}\:\:\Rightarrow\:\:\mathrm{3}\lambda^{\mathrm{2}} −\mathrm{2}\lambda−\mathrm{5}=\mathrm{0} \\ $$$$\lambda=\frac{\mathrm{1}}{\mathrm{3}}+\sqrt{\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{5}}{\mathrm{3}}}\:=\:\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\left(\mathrm{2}{a}−{r}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +\left(\mathrm{2}{b}+{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{3}{a}^{\mathrm{2}} −\mathrm{4}{ar}=\mathrm{4}{b}^{\mathrm{2}} +\mathrm{4}{br} \\ $$$${r}=\frac{\mathrm{3}{a}^{\mathrm{2}} −\mathrm{4}{b}^{\mathrm{2}} }{\mathrm{4}\left({a}+{b}\right)}=\frac{{a}\left(\mathrm{3}×\frac{\mathrm{25}}{\mathrm{9}}−\mathrm{4}\right)}{\mathrm{4}\left(\frac{\mathrm{5}}{\mathrm{3}}+\mathrm{1}\right)} \\ $$$$\:\:\:=\:\frac{\mathrm{13}{a}}{\mathrm{32}}\:=\:\frac{\mathrm{65}}{\mathrm{32}}\:. \\ $$$$ \\ $$
Commented by ajfour last updated on 26/Jan/20
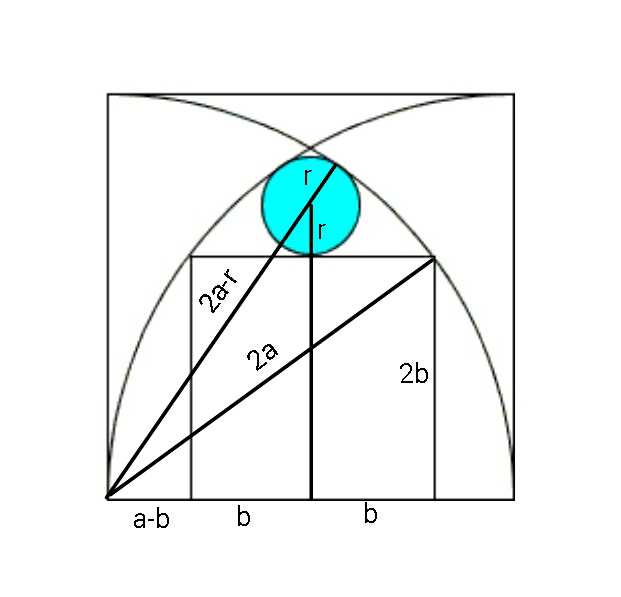
Commented by mr W last updated on 26/Jan/20
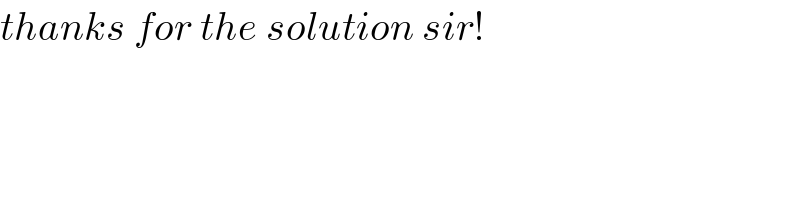
$${thanks}\:{for}\:{the}\:{solution}\:{sir}! \\ $$
