Question Number 79634 by TawaTawa last updated on 26/Jan/20
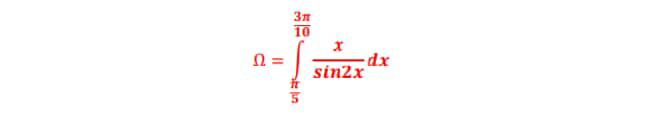
Commented by mathmax by abdo last updated on 27/Jan/20
![Ω =∫_(π/5) ^((3π)/(10)) (x/(sin(2x)))dx changement x=(π/2)−t givet=(π/2)−x Ω=∫_((3π)/(10)) ^(π/5) (((π/2)−t)/(sin(2t)))(−dt) =(π/2)∫_(π/5) ^((3π)/(10)) (dt/(sin(2t))) −Ω ⇒ 2Ω =(π/2) ∫_(π/5) ^((3π)/(10)) (dt/(sin(2t))) changement tant =u give ∫_(π/5) ^((3π)/(10)) (dt/(sin(2t))) =∫_(tan((π/5))) ^(tan(((3π)/(10)))) (1/((2u)/(1+u^2 )))×(du/(1+u^2 )) =(1/2)[ln∣u∣]_(tan((π/5))) ^(tan(((3π)/(10)))) =(1/2){ln(tan(((3π)/(10)))−ln(tan((π/5)))} =(1/2){ ln(tan((π/2)−(π/5)))−ln(tan((π/5)))} =(1/2){ln((1/(tan((π/5)))))−ln(tan((π/5)))}=−ln(tan((π/5))) ⇒ Ω=−(π/4)ln(tan((π/5)))](https://www.tinkutara.com/question/Q79687.png)
$$\Omega\:=\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \:\frac{{x}}{{sin}\left(\mathrm{2}{x}\right)}{dx}\:\:{changement}\:{x}=\frac{\pi}{\mathrm{2}}−{t}\:{givet}=\frac{\pi}{\mathrm{2}}−{x} \\ $$$$\Omega=\int_{\frac{\mathrm{3}\pi}{\mathrm{10}}} ^{\frac{\pi}{\mathrm{5}}} \:\frac{\frac{\pi}{\mathrm{2}}−{t}}{{sin}\left(\mathrm{2}{t}\right)}\left(−{dt}\right)\:=\frac{\pi}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \:\frac{{dt}}{{sin}\left(\mathrm{2}{t}\right)}\:−\Omega\:\Rightarrow \\ $$$$\mathrm{2}\Omega\:=\frac{\pi}{\mathrm{2}}\:\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \:\frac{{dt}}{{sin}\left(\mathrm{2}{t}\right)}\:\:{changement}\:{tant}\:={u}\:{give} \\ $$$$\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \:\frac{{dt}}{{sin}\left(\mathrm{2}{t}\right)}\:=\int_{{tan}\left(\frac{\pi}{\mathrm{5}}\right)} ^{{tan}\left(\frac{\mathrm{3}\pi}{\mathrm{10}}\right)} \:\:\frac{\mathrm{1}}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}×\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid{u}\mid\right]_{{tan}\left(\frac{\pi}{\mathrm{5}}\right)} ^{{tan}\left(\frac{\mathrm{3}\pi}{\mathrm{10}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left({tan}\left(\frac{\mathrm{3}\pi}{\mathrm{10}}\right)−{ln}\left({tan}\left(\frac{\pi}{\mathrm{5}}\right)\right)\right\}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:{ln}\left({tan}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{5}}\right)\right)−{ln}\left({tan}\left(\frac{\pi}{\mathrm{5}}\right)\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\frac{\mathrm{1}}{{tan}\left(\frac{\pi}{\mathrm{5}}\right)}\right)−{ln}\left({tan}\left(\frac{\pi}{\mathrm{5}}\right)\right)\right\}=−{ln}\left({tan}\left(\frac{\pi}{\mathrm{5}}\right)\right)\:\Rightarrow \\ $$$$\Omega=−\frac{\pi}{\mathrm{4}}{ln}\left({tan}\left(\frac{\pi}{\mathrm{5}}\right)\right) \\ $$
Commented by TawaTawa last updated on 27/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 29/Jan/20

$${you}\:{are}\:{welcome} \\ $$
Answered by mind is power last updated on 27/Jan/20
![Ω=∫_(π/5) ^((3π)/(10)) (x/(sin(2x)))dx ∫_a ^b f(x)dx=∫_a ^b f(a+b−x)dx⇒ ∫_(π/5) ^((3π)/(10)) (((π/2)−x)/(sin(2((π/2)−x))))dx=∫_(π/5) ^((3π)/(10)) (((π/2)−x)/(sin(π−2x)))dx=−∫_(π/5) ^((3π)/(10)) (x/(sin(2x)))+ (π/2)∫_(π/5) ^((3π)/(10)) (dx/(sin(2x)))⇒ ⇒2∫_(π/5) ^((3π)/(10)) ((xdx)/(sin(2x)))=(π/2)∫_(π/5) ^((3π)/(10)) (dx/(sin(2x)))=(π/4)∫_(π/5) ^((3π)/(10)) (dx/(sin(x)cos(x))) =(π/4)∫_(π/5) ^((3π)/(10)) ((cos(x))/(sin(x).cos^2 (x)))dx=(π/4)∫_(π/5) ^((3π)/(10)) cot(x).(1+tg^2 (x))dx =(π/4)∫_(π/5) ^((3π)/(10)) tg((π/2)−x)d(tg(x)) =(π/8)[−tg^2 ((π/2)−x)]_(π/5) ^((3π)/(10)) =−(π/8)(tg^2 ((π/5))−tg^2 (((3π)/(10)))) we can find exact tg((π/5)),and tg(((3π)/(10)))](https://www.tinkutara.com/question/Q79654.png)
$$\Omega=\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{{x}}{{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx}\Rightarrow \\ $$$$\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{\frac{\pi}{\mathrm{2}}−{x}}{{sin}\left(\mathrm{2}\left(\frac{\pi}{\mathrm{2}}−{x}\right)\right)}{dx}=\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{\frac{\pi}{\mathrm{2}}−{x}}{{sin}\left(\pi−\mathrm{2}{x}\right)}{dx}=−\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{{x}}{{sin}\left(\mathrm{2}{x}\right)}+ \\ $$$$\frac{\pi}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{{dx}}{{sin}\left(\mathrm{2}{x}\right)}\Rightarrow \\ $$$$\Rightarrow\mathrm{2}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{{xdx}}{{sin}\left(\mathrm{2}{x}\right)}=\frac{\pi}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{{dx}}{{sin}\left(\mathrm{2}{x}\right)}=\frac{\pi}{\mathrm{4}}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{{dx}}{{sin}\left({x}\right){cos}\left({x}\right)} \\ $$$$=\frac{\pi}{\mathrm{4}}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} \frac{{cos}\left({x}\right)}{{sin}\left({x}\right).{cos}^{\mathrm{2}} \left({x}\right)}{dx}=\frac{\pi}{\mathrm{4}}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} {cot}\left({x}\right).\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)\right){dx} \\ $$$$=\frac{\pi}{\mathrm{4}}\int_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} {tg}\left(\frac{\pi}{\mathrm{2}}−{x}\right){d}\left({tg}\left({x}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{8}}\left[−{tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)\right]_{\frac{\pi}{\mathrm{5}}} ^{\frac{\mathrm{3}\pi}{\mathrm{10}}} =−\frac{\pi}{\mathrm{8}}\left({tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{5}}\right)−{tg}^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{10}}\right)\right) \\ $$$${we}\:{can}\:{find}\:\:{exact}\:{tg}\left(\frac{\pi}{\mathrm{5}}\right),{and}\:{tg}\left(\frac{\mathrm{3}\pi}{\mathrm{10}}\right) \\ $$$$ \\ $$
Commented by TawaTawa last updated on 27/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mind is power last updated on 27/Jan/20
$${thak}\:{you}\:,{withe}\:{pleasur} \\ $$
