Question Number 79675 by ajfour last updated on 27/Jan/20

Commented by ajfour last updated on 27/Jan/20

$${The}\:{square}\:{has}\:{side}\:{s}. \\ $$$${Can}\:{we}\:{find}\:{a}\:{set}\:{of}\:{radii}\:{values}? \\ $$
Commented by ajfour last updated on 27/Jan/20

Commented by ajfour last updated on 27/Jan/20
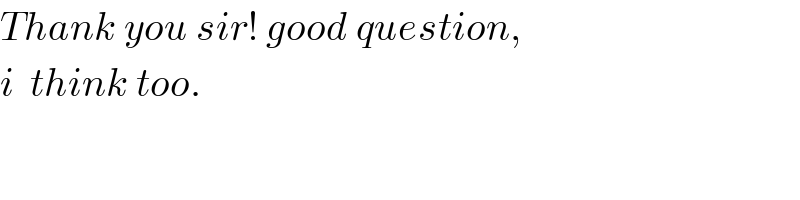
$${Thank}\:{you}\:{sir}!\:{good}\:{question}, \\ $$$${i}\:\:{think}\:{too}. \\ $$
Commented by mr W last updated on 27/Jan/20

$${let}\:{c}=\lambda{s} \\ $$$$\left({a}+{c}\right)^{\mathrm{2}} −\left({a}−{c}\right)^{\mathrm{2}} =\left({s}−{c}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{ac}=\left({s}−{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{a}=\frac{\left({s}−{c}\right)^{\mathrm{2}} }{\mathrm{4}{c}}=\frac{\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} {s}}{\mathrm{4}\lambda} \\ $$$$ \\ $$$$\left({b}+{c}\right)^{\mathrm{2}} −\left({s}−{b}−{c}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\mathrm{2}{bs}=\left({s}−{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{b}=\frac{\left({s}−{c}\right)^{\mathrm{2}} }{\mathrm{2}{s}}=\frac{\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} {s}}{\mathrm{2}} \\ $$$$ \\ $$$${a}+{b}={s} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} }{\mathrm{4}\lambda}+\frac{\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \left(\mathrm{2}\lambda+\mathrm{1}\right)=\mathrm{4}\lambda \\ $$$$\Rightarrow\mathrm{2}\lambda^{\mathrm{3}} −\mathrm{3}\lambda^{\mathrm{2}} −\mathrm{4}\lambda+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\lambda+\mathrm{1}\right)\left(\mathrm{2}\lambda^{\mathrm{2}} −\mathrm{5}\lambda+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda=−\mathrm{1}<\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{5}\pm\sqrt{\mathrm{17}}}{\mathrm{4}}\:\:{should}\:<\mathrm{1} \\ $$$$\Rightarrow{there}\:{is}\:{only}\:{one}\:{set}\:{of}\:{radii}\:{with} \\ $$$$\lambda=\frac{\mathrm{5}−\sqrt{\mathrm{17}}}{\mathrm{4}}\approx\mathrm{0}.\mathrm{219} \\ $$$${a}=\frac{\left(\mathrm{7}+\sqrt{\mathrm{17}}\right){s}}{\mathrm{16}}\approx\mathrm{0}.\mathrm{695}{s} \\ $$$${b}=\frac{\left(\mathrm{9}−\sqrt{\mathrm{17}}\right){s}}{\mathrm{16}}\approx\mathrm{0}.\mathrm{305}{s} \\ $$$${c}=\frac{\left(\mathrm{5}−\sqrt{\mathrm{17}}\right){s}}{\mathrm{4}}\approx\mathrm{0}.\mathrm{219}{s} \\ $$
Commented by mr W last updated on 27/Jan/20

$${nice}\:{question}! \\ $$
Commented by MJS last updated on 27/Jan/20

$$\mathrm{can}\:\mathrm{we}\:\mathrm{find}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{when}\:{AB}\:\mathrm{is}\:\mathrm{not}\:\mathrm{parallel} \\ $$$$\mathrm{to}\:{s}?\:\mathrm{it}\:\mathrm{might}\:\mathrm{get}\:\mathrm{hard}… \\ $$
Commented by ajfour last updated on 27/Jan/20

$${it}\:{came}\:{out}\:{automatically}, \\ $$$${question}\:{did}\:{not}\:{give}\:{such}\:{a} \\ $$$${condition},\:{Sir}. \\ $$
Commented by mr W last updated on 27/Jan/20

$${since}\:{centers}\:{A}\:{and}\:{B}\:{are}\:{on}\:{the} \\ $$$${opposite}\:{sides},\:{we}\:{have}\:{automatically} \\ $$$${a}+{b}={s}. \\ $$
Commented by MJS last updated on 27/Jan/20

$$\mathrm{ok} \\ $$
Commented by mr W last updated on 27/Jan/20

$${MJS}\:{sir}:\:{do}\:{you}\:{have}\:{experience}\:{with} \\ $$$${trilinear}\:{coordinates}\:{system}?\:{can}\:{it} \\ $$$${be}\:{helpful}\:{to}\:{solve}\:{Q}\mathrm{79694}?\:{thanks}! \\ $$
Commented by MJS last updated on 27/Jan/20

$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{help} \\ $$
