Menu Close

Question-79697

Tinku Tara 0 Comments
Pin




Question Number 79697 by ajfour last updated on 27/Jan/20
Commented by ajfour last updated on 27/Jan/20
Find coordinates of A,B,C if each coloured regions I→IV have the same area.
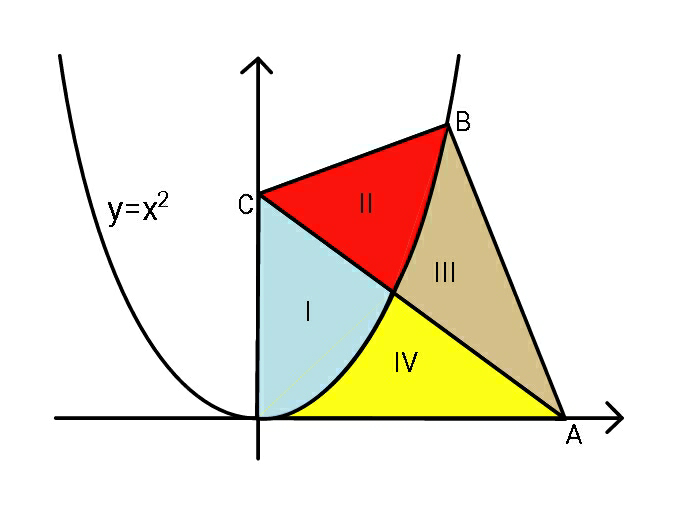
$${Find}\:{coordinates}\:{of}\:{A},{B},{C}\:{if} \\ $$$${each}\:{coloured}\:{regions}\:{I}\rightarrow{IV} \\ $$$${have}\:{the}\:{same}\:{area}. \\ $$
Answered by ajfour last updated on 27/Jan/20
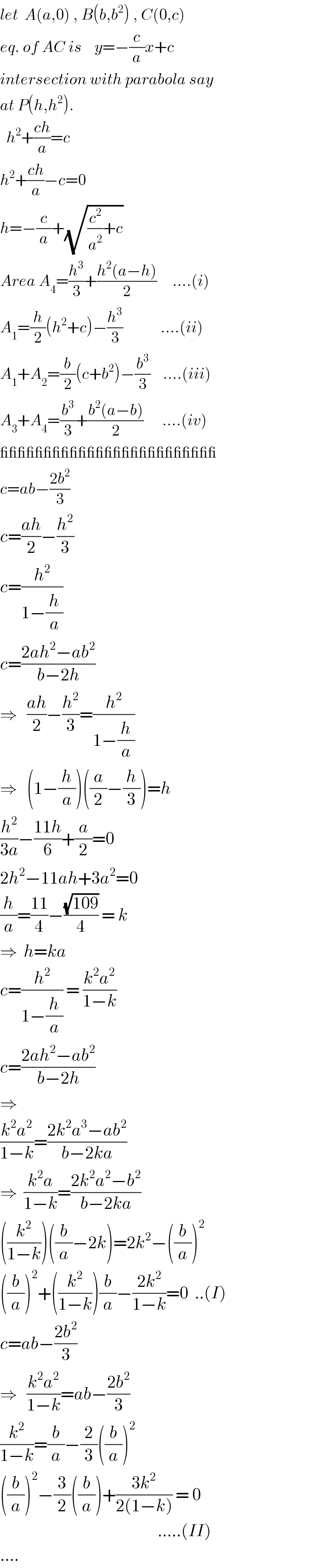
let A(a,0) , B(b,b^2 ) , C(0,c) eq. of AC is y=−(c/a)x+c intersection with parabola say at P(h,h^2 ). h^2 +((ch)/a)=c h^2 +((ch)/a)−c=0 h=−(c/a)+(√((c^2 /a^2 )+c)) Area A_4 =(h^3 /3)+((h^2 (a−h))/2) ....(i) A_1 =(h/2)(h^2 +c)−(h^3 /3) ....(ii) A_1 +A_2 =(b/2)(c+b^2 )−(b^3 /3) ....(iii) A_3 +A_4 =(b^3 /3)+((b^2 (a−b))/2) ....(iv) _________________________ c=ab−((2b^2 )/3) c=((ah)/2)−(h^2 /3) c=(h^2 /(1−(h/a))) c=((2ah^2 −ab^2 )/(b−2h)) ⇒ ((ah)/2)−(h^2 /3)=(h^2 /(1−(h/a))) ⇒ (1−(h/a))((a/2)−(h/3))=h (h^2 /(3a))−((11h)/6)+(a/2)=0 2h^2 −11ah+3a^2 =0 (h/a)=((11)/4)−((√(109))/4) = k ⇒ h=ka c=(h^2 /(1−(h/a))) = ((k^2 a^2 )/(1−k)) c=((2ah^2 −ab^2 )/(b−2h)) ⇒ ((k^2 a^2 )/(1−k))=((2k^2 a^3 −ab^2 )/(b−2ka)) ⇒ ((k^2 a)/(1−k))=((2k^2 a^2 −b^2 )/(b−2ka)) ((k^2 /(1−k)))((b/a)−2k)=2k^2 −((b/a))^2 ((b/a))^2 +((k^2 /(1−k)))(b/a)−((2k^2 )/(1−k))=0 ..(I) c=ab−((2b^2 )/3) ⇒ ((k^2 a^2 )/(1−k))=ab−((2b^2 )/3) (k^2 /(1−k))=(b/a)−(2/3)((b/a))^2 ((b/a))^2 −(3/2)((b/a))+((3k^2 )/(2(1−k))) = 0 .....(II) ....
$${let}\:\:{A}\left({a},\mathrm{0}\right)\:,\:{B}\left({b},{b}^{\mathrm{2}} \right)\:,\:{C}\left(\mathrm{0},{c}\right) \\ $$$${eq}.\:{of}\:{AC}\:{is}\:\:\:\:{y}=−\frac{{c}}{{a}}{x}+{c} \\ $$$${intersection}\:{with}\:{parabola}\:{say} \\ $$$${at}\:{P}\left({h},{h}^{\mathrm{2}} \right). \\ $$$$\:\:{h}^{\mathrm{2}} +\frac{{ch}}{{a}}={c} \\ $$$${h}^{\mathrm{2}} +\frac{{ch}}{{a}}−{c}=\mathrm{0} \\ $$$${h}=−\frac{{c}}{{a}}+\sqrt{\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+{c}} \\ $$$${Area}\:{A}_{\mathrm{4}} =\frac{{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{h}^{\mathrm{2}} \left({a}−{h}\right)}{\mathrm{2}}\:\:\:\:\:….\left({i}\right) \\ $$$${A}_{\mathrm{1}} =\frac{{h}}{\mathrm{2}}\left({h}^{\mathrm{2}} +{c}\right)−\frac{{h}^{\mathrm{3}} }{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$${A}_{\mathrm{1}} +{A}_{\mathrm{2}} =\frac{{b}}{\mathrm{2}}\left({c}+{b}^{\mathrm{2}} \right)−\frac{{b}^{\mathrm{3}} }{\mathrm{3}}\:\:\:\:….\left({iii}\right) \\ $$$${A}_{\mathrm{3}} +{A}_{\mathrm{4}} =\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} \left({a}−{b}\right)}{\mathrm{2}}\:\:\:\:\:\:….\left({iv}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${c}={ab}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${c}=\frac{{ah}}{\mathrm{2}}−\frac{{h}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${c}=\frac{{h}^{\mathrm{2}} }{\mathrm{1}−\frac{{h}}{{a}}} \\ $$$${c}=\frac{\mathrm{2}{ah}^{\mathrm{2}} −{ab}^{\mathrm{2}} }{{b}−\mathrm{2}{h}} \\ $$$$\Rightarrow\:\:\:\frac{{ah}}{\mathrm{2}}−\frac{{h}^{\mathrm{2}} }{\mathrm{3}}=\frac{{h}^{\mathrm{2}} }{\mathrm{1}−\frac{{h}}{{a}}} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{1}−\frac{{h}}{{a}}\right)\left(\frac{{a}}{\mathrm{2}}−\frac{{h}}{\mathrm{3}}\right)={h} \\ $$$$\frac{{h}^{\mathrm{2}} }{\mathrm{3}{a}}−\frac{\mathrm{11}{h}}{\mathrm{6}}+\frac{{a}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{2}{h}^{\mathrm{2}} −\mathrm{11}{ah}+\mathrm{3}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{h}}{{a}}=\frac{\mathrm{11}}{\mathrm{4}}−\frac{\sqrt{\mathrm{109}}}{\mathrm{4}}\:=\:{k} \\ $$$$\Rightarrow\:\:{h}={ka} \\ $$$${c}=\frac{{h}^{\mathrm{2}} }{\mathrm{1}−\frac{{h}}{{a}}}\:=\:\frac{{k}^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{1}−{k}} \\ $$$${c}=\frac{\mathrm{2}{ah}^{\mathrm{2}} −{ab}^{\mathrm{2}} }{{b}−\mathrm{2}{h}} \\ $$$$\Rightarrow\:\: \\ $$$$\frac{{k}^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{1}−{k}}=\frac{\mathrm{2}{k}^{\mathrm{2}} {a}^{\mathrm{3}} −{ab}^{\mathrm{2}} }{{b}−\mathrm{2}{ka}} \\ $$$$\Rightarrow\:\:\frac{{k}^{\mathrm{2}} {a}}{\mathrm{1}−{k}}=\frac{\mathrm{2}{k}^{\mathrm{2}} {a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{b}−\mathrm{2}{ka}} \\ $$$$\left(\frac{{k}^{\mathrm{2}} }{\mathrm{1}−{k}}\right)\left(\frac{{b}}{{a}}−\mathrm{2}{k}\right)=\mathrm{2}{k}^{\mathrm{2}} −\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} \\ $$$$\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} +\left(\frac{{k}^{\mathrm{2}} }{\mathrm{1}−{k}}\right)\frac{{b}}{{a}}−\frac{\mathrm{2}{k}^{\mathrm{2}} }{\mathrm{1}−{k}}=\mathrm{0}\:\:..\left({I}\right) \\ $$$${c}={ab}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:\frac{{k}^{\mathrm{2}} {a}^{\mathrm{2}} }{\mathrm{1}−{k}}={ab}−\frac{\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\frac{{k}^{\mathrm{2}} }{\mathrm{1}−{k}}=\frac{{b}}{{a}}−\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} \:\:\: \\ $$$$\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{{b}}{{a}}\right)+\frac{\mathrm{3}{k}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}−{k}\right)}\:=\:\mathrm{0}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left({II}\right) \\ $$$$…. \\ $$
Commented by ajfour last updated on 27/Jan/20
I just have to check, seems sure, that they′ll conflict..
$${I}\:{just}\:{have}\:{to}\:{check},\:{seems} \\ $$$${sure},\:{that}\:{they}'{ll}\:{conflict}.. \\ $$
Answered by mr W last updated on 28/Jan/20
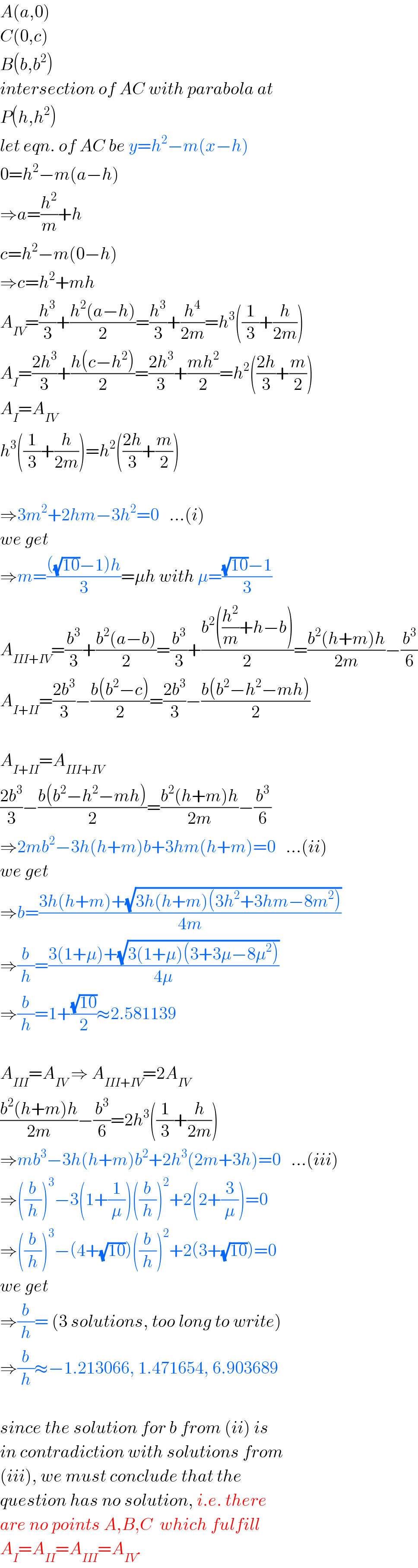
A(a,0) C(0,c) B(b,b^2 ) intersection of AC with parabola at P(h,h^2 ) let eqn. of AC be y=h^2 −m(x−h) 0=h^2 −m(a−h) ⇒a=(h^2 /m)+h c=h^2 −m(0−h) ⇒c=h^2 +mh A_(IV) =(h^3 /3)+((h^2 (a−h))/2)=(h^3 /3)+(h^4 /(2m))=h^3 ((1/3)+(h/(2m))) A_I =((2h^3 )/3)+((h(c−h^2 ))/2)=((2h^3 )/3)+((mh^2 )/2)=h^2 (((2h)/3)+(m/2)) A_I =A_(IV) h^3 ((1/3)+(h/(2m)))=h^2 (((2h)/3)+(m/2)) ⇒3m^2 +2hm−3h^2 =0 ...(i) we get ⇒m=((((√(10))−1)h)/3)=μh with μ=(((√(10))−1)/3) A_(III+IV) =(b^3 /3)+((b^2 (a−b))/2)=(b^3 /3)+((b^2 ((h^2 /m)+h−b))/2)=((b^2 (h+m)h)/(2m))−(b^3 /6) A_(I+II) =((2b^3 )/3)−((b(b^2 −c))/2)=((2b^3 )/3)−((b(b^2 −h^2 −mh))/2) A_(I+II) =A_(III+IV) ((2b^3 )/3)−((b(b^2 −h^2 −mh))/2)=((b^2 (h+m)h)/(2m))−(b^3 /6) ⇒2mb^2 −3h(h+m)b+3hm(h+m)=0 ...(ii) we get ⇒b=((3h(h+m)+(√(3h(h+m)(3h^2 +3hm−8m^2 ))))/(4m)) ⇒(b/h)=((3(1+μ)+(√(3(1+μ)(3+3μ−8μ^2 ))))/(4μ)) ⇒(b/h)=1+((√(10))/2)≈2.581139 A_(III) =A_(IV) ⇒ A_(III+IV) =2A_(IV) ((b^2 (h+m)h)/(2m))−(b^3 /6)=2h^3 ((1/3)+(h/(2m))) ⇒mb^3 −3h(h+m)b^2 +2h^3 (2m+3h)=0 ...(iii) ⇒((b/h))^3 −3(1+(1/μ))((b/h))^2 +2(2+(3/μ))=0 ⇒((b/h))^3 −(4+(√(10)))((b/h))^2 +2(3+(√(10)))=0 we get ⇒(b/h)= (3 solutions, too long to write) ⇒(b/h)≈−1.213066, 1.471654, 6.903689 since the solution for b from (ii) is in contradiction with solutions from (iii), we must conclude that the question has no solution, i.e. there are no points A,B,C which fulfill A_I =A_(II) =A_(III) =A_(IV) .
$${A}\left({a},\mathrm{0}\right) \\ $$$${C}\left(\mathrm{0},{c}\right) \\ $$$${B}\left({b},{b}^{\mathrm{2}} \right) \\ $$$${intersection}\:{of}\:{AC}\:{with}\:{parabola}\:{at} \\ $$$${P}\left({h},{h}^{\mathrm{2}} \right) \\ $$$${let}\:{eqn}.\:{of}\:{AC}\:{be}\:{y}={h}^{\mathrm{2}} −{m}\left({x}−{h}\right) \\ $$$$\mathrm{0}={h}^{\mathrm{2}} −{m}\left({a}−{h}\right) \\ $$$$\Rightarrow{a}=\frac{{h}^{\mathrm{2}} }{{m}}+{h} \\ $$$${c}={h}^{\mathrm{2}} −{m}\left(\mathrm{0}−{h}\right) \\ $$$$\Rightarrow{c}={h}^{\mathrm{2}} +{mh} \\ $$$${A}_{{IV}} =\frac{{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{h}^{\mathrm{2}} \left({a}−{h}\right)}{\mathrm{2}}=\frac{{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{h}^{\mathrm{4}} }{\mathrm{2}{m}}={h}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{{h}}{\mathrm{2}{m}}\right) \\ $$$${A}_{{I}} =\frac{\mathrm{2}{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{h}\left({c}−{h}^{\mathrm{2}} \right)}{\mathrm{2}}=\frac{\mathrm{2}{h}^{\mathrm{3}} }{\mathrm{3}}+\frac{{mh}^{\mathrm{2}} }{\mathrm{2}}={h}^{\mathrm{2}} \left(\frac{\mathrm{2}{h}}{\mathrm{3}}+\frac{{m}}{\mathrm{2}}\right) \\ $$$${A}_{{I}} ={A}_{{IV}} \\ $$$${h}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{{h}}{\mathrm{2}{m}}\right)={h}^{\mathrm{2}} \left(\frac{\mathrm{2}{h}}{\mathrm{3}}+\frac{{m}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\Rightarrow\mathrm{3}{m}^{\mathrm{2}} +\mathrm{2}{hm}−\mathrm{3}{h}^{\mathrm{2}} =\mathrm{0}\:\:\:…\left({i}\right) \\ $$$${we}\:{get} \\ $$$$\Rightarrow{m}=\frac{\left(\sqrt{\mathrm{10}}−\mathrm{1}\right){h}}{\mathrm{3}}=\mu{h}\:{with}\:\mu=\frac{\sqrt{\mathrm{10}}−\mathrm{1}}{\mathrm{3}} \\ $$$${A}_{{III}+{IV}} =\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} \left({a}−{b}\right)}{\mathrm{2}}=\frac{{b}^{\mathrm{3}} }{\mathrm{3}}+\frac{{b}^{\mathrm{2}} \left(\frac{{h}^{\mathrm{2}} }{{m}}+{h}−{b}\right)}{\mathrm{2}}=\frac{{b}^{\mathrm{2}} \left({h}+{m}\right){h}}{\mathrm{2}{m}}−\frac{{b}^{\mathrm{3}} }{\mathrm{6}} \\ $$$${A}_{{I}+{II}} =\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{3}}−\frac{{b}\left({b}^{\mathrm{2}} −{c}\right)}{\mathrm{2}}=\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{3}}−\frac{{b}\left({b}^{\mathrm{2}} −{h}^{\mathrm{2}} −{mh}\right)}{\mathrm{2}} \\ $$$$ \\ $$$${A}_{{I}+{II}} ={A}_{{III}+{IV}} \\ $$$$\frac{\mathrm{2}{b}^{\mathrm{3}} }{\mathrm{3}}−\frac{{b}\left({b}^{\mathrm{2}} −{h}^{\mathrm{2}} −{mh}\right)}{\mathrm{2}}=\frac{{b}^{\mathrm{2}} \left({h}+{m}\right){h}}{\mathrm{2}{m}}−\frac{{b}^{\mathrm{3}} }{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{2}{mb}^{\mathrm{2}} −\mathrm{3}{h}\left({h}+{m}\right){b}+\mathrm{3}{hm}\left({h}+{m}\right)=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$${we}\:{get} \\ $$$$\Rightarrow{b}=\frac{\mathrm{3}{h}\left({h}+{m}\right)+\sqrt{\mathrm{3}{h}\left({h}+{m}\right)\left(\mathrm{3}{h}^{\mathrm{2}} +\mathrm{3}{hm}−\mathrm{8}{m}^{\mathrm{2}} \right)}}{\mathrm{4}{m}} \\ $$$$\Rightarrow\frac{{b}}{{h}}=\frac{\mathrm{3}\left(\mathrm{1}+\mu\right)+\sqrt{\mathrm{3}\left(\mathrm{1}+\mu\right)\left(\mathrm{3}+\mathrm{3}\mu−\mathrm{8}\mu^{\mathrm{2}} \right)}}{\mathrm{4}\mu} \\ $$$$\Rightarrow\frac{{b}}{{h}}=\mathrm{1}+\frac{\sqrt{\mathrm{10}}}{\mathrm{2}}\approx\mathrm{2}.\mathrm{581139} \\ $$$$ \\ $$$${A}_{{III}} ={A}_{{IV}} \:\Rightarrow\:{A}_{{III}+{IV}} =\mathrm{2}{A}_{{IV}} \\ $$$$\frac{{b}^{\mathrm{2}} \left({h}+{m}\right){h}}{\mathrm{2}{m}}−\frac{{b}^{\mathrm{3}} }{\mathrm{6}}=\mathrm{2}{h}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{{h}}{\mathrm{2}{m}}\right) \\ $$$$\Rightarrow{mb}^{\mathrm{3}} −\mathrm{3}{h}\left({h}+{m}\right){b}^{\mathrm{2}} +\mathrm{2}{h}^{\mathrm{3}} \left(\mathrm{2}{m}+\mathrm{3}{h}\right)=\mathrm{0}\:\:\:…\left({iii}\right) \\ $$$$\Rightarrow\left(\frac{{b}}{{h}}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{1}+\frac{\mathrm{1}}{\mu}\right)\left(\frac{{b}}{{h}}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{2}+\frac{\mathrm{3}}{\mu}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\frac{{b}}{{h}}\right)^{\mathrm{3}} −\left(\mathrm{4}+\sqrt{\mathrm{10}}\right)\left(\frac{{b}}{{h}}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{3}+\sqrt{\mathrm{10}}\right)=\mathrm{0} \\ $$$${we}\:{get} \\ $$$$\Rightarrow\frac{{b}}{{h}}=\:\left(\mathrm{3}\:{solutions},\:{too}\:{long}\:{to}\:{write}\right) \\ $$$$\Rightarrow\frac{{b}}{{h}}\approx−\mathrm{1}.\mathrm{213066},\:\mathrm{1}.\mathrm{471654},\:\mathrm{6}.\mathrm{903689} \\ $$$$ \\ $$$${since}\:{the}\:{solution}\:{for}\:{b}\:{from}\:\left({ii}\right)\:{is} \\ $$$${in}\:{contradiction}\:{with}\:{solutions}\:{from} \\ $$$$\left({iii}\right),\:{we}\:{must}\:{conclude}\:{that}\:{the} \\ $$$${question}\:{has}\:{no}\:{solution},\:{i}.{e}.\:{there} \\ $$$${are}\:{no}\:{points}\:{A},{B},{C}\:\:{which}\:{fulfill}\: \\ $$$${A}_{{I}} ={A}_{{II}} ={A}_{{III}} ={A}_{{IV}} . \\ $$
Commented by john santu last updated on 27/Jan/20
AC : cx + ay = ac
$$\mathrm{AC}\::\:\mathrm{cx}\:+\:\mathrm{ay}\:=\:\mathrm{ac}\: \\ $$
Commented by mr W last updated on 28/Jan/20
for AC i use the equation in form of y=h^2 −m(x−h). it goes through point P(h,h^2 ) [the same as D(d,d^2 ) in your workings] and has the inclination −m. such that A_I =A_(IV) we have m=((((√(10))−1)h)/3).
$${for}\:{AC}\:{i}\:{use}\:{the}\:{equation}\:{in}\:{form}\:{of} \\ $$$${y}={h}^{\mathrm{2}} −{m}\left({x}−{h}\right). \\ $$$${it}\:{goes}\:{through}\:{point}\:{P}\left({h},{h}^{\mathrm{2}} \right)\:\left[{the}\:{same}\right. \\ $$$$\left.{as}\:{D}\left({d},{d}^{\mathrm{2}} \right)\:{in}\:{your}\:{workings}\right]\:{and}\:{has} \\ $$$${the}\:{inclination}\:−{m}. \\ $$$${such}\:{that}\:{A}_{{I}} ={A}_{{IV}} \:{we}\:{have} \\ $$$${m}=\frac{\left(\sqrt{\mathrm{10}}−\mathrm{1}\right){h}}{\mathrm{3}}. \\ $$
Commented by ajfour last updated on 28/Jan/20
unfortunately a no solution question, thanks for attempting sir.
$${unfortunately}\:{a}\:{no}\:{solution} \\ $$$${question},\:{thanks}\:{for} \\ $$$${attempting}\:{sir}. \\ $$
Commented by mr W last updated on 28/Jan/20
but it′s again a very challenging question whose solution is not so obvious at first glance. one can really learn through such questions. therefore thanks alot sir!
$${but}\:{it}'{s}\:{again}\:{a}\:{very}\:{challenging}\: \\ $$$${question}\:{whose}\:{solution}\:{is}\:{not}\:{so} \\ $$$${obvious}\:{at}\:{first}\:{glance}.\:{one}\:{can}\:{really} \\ $$$${learn}\:{through}\:{such}\:{questions}. \\ $$$${therefore}\:{thanks}\:{alot}\:{sir}! \\ $$
Commented by john santu last updated on 28/Jan/20
this case closed?
$$\mathrm{this}\:\mathrm{case}\:\mathrm{closed}? \\ $$
Commented by mr W last updated on 28/Jan/20
Commented by mr W last updated on 28/Jan/20
here more explanation why there is no solution for this question. for every point P(h,h^2 ) we can find point A(a,0) and C(0,c) such that A_I =A_(IV) when a=(1+(1/μ))h and c=(1+μ)h^2 . with μ=(((√(10))−1)/3)=constant. for every point P(h,h^2 ) we can find one point B, say B_1 (b_1 ,b_1 ^2 ), such that A_(II) =A_(III) when b_1 =2.581139h (exact value possible) for every point P(h,h^2 ) we can find two points B, say B_2 (b_2 ,b_2 ^2 ) and B_3 (b_3 ,b_3 ^2 ), such that A_(III) =A_(IV) when b_2 =1.471654h (exact value possible) b_3 =6.903689h (exact value possible) we see that we can not select the point P, i.e. find a value for h such that B_1 coincides with B_2 or B_3 , that means it′s impossible to get A_I =A_(II) =A_(III) =A_(IV) .
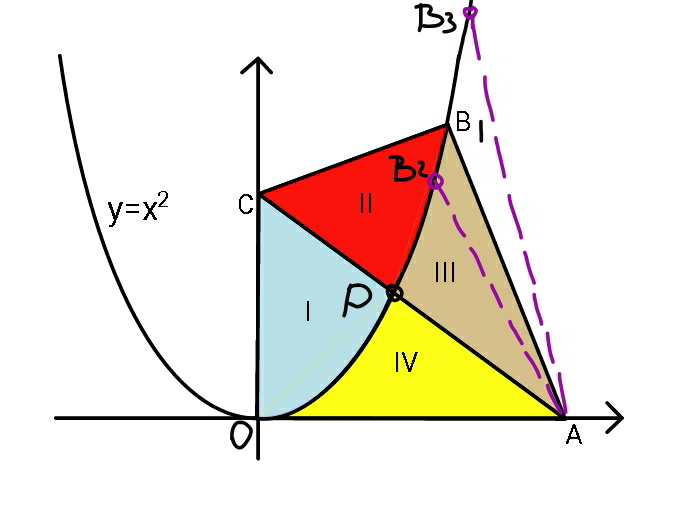
$${here}\:{more}\:{explanation}\:{why}\:{there}\:{is} \\ $$$${no}\:{solution}\:{for}\:{this}\:{question}. \\ $$$$ \\ $$$${for}\:{every}\:{point}\:{P}\left({h},{h}^{\mathrm{2}} \right)\:{we}\:{can}\:{find} \\ $$$${point}\:{A}\left({a},\mathrm{0}\right)\:{and}\:{C}\left(\mathrm{0},{c}\right)\:{such}\:{that} \\ $$$${A}_{{I}} ={A}_{{IV}} \:{when} \\ $$$${a}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mu}\right){h}\:{and}\:{c}=\left(\mathrm{1}+\mu\right){h}^{\mathrm{2}} . \\ $$$${with}\:\mu=\frac{\sqrt{\mathrm{10}}−\mathrm{1}}{\mathrm{3}}={constant}. \\ $$$$ \\ $$$${for}\:{every}\:{point}\:{P}\left({h},{h}^{\mathrm{2}} \right)\:{we}\:{can}\:{find} \\ $$$${one}\:{point}\:{B},\:{say}\:{B}_{\mathrm{1}} \left({b}_{\mathrm{1}} ,{b}_{\mathrm{1}} ^{\mathrm{2}} \right),\:{such}\:{that} \\ $$$${A}_{{II}} ={A}_{{III}} \:{when} \\ $$$${b}_{\mathrm{1}} =\mathrm{2}.\mathrm{581139}{h}\:\left({exact}\:{value}\:{possible}\right) \\ $$$$ \\ $$$${for}\:{every}\:{point}\:{P}\left({h},{h}^{\mathrm{2}} \right)\:{we}\:{can}\:{find} \\ $$$${two}\:{points}\:{B},\:{say}\:{B}_{\mathrm{2}} \left({b}_{\mathrm{2}} ,{b}_{\mathrm{2}} ^{\mathrm{2}} \right)\:{and} \\ $$$${B}_{\mathrm{3}} \left({b}_{\mathrm{3}} ,{b}_{\mathrm{3}} ^{\mathrm{2}} \right),\:{such}\:{that} \\ $$$${A}_{{III}} ={A}_{{IV}} \:\:{when} \\ $$$${b}_{\mathrm{2}} =\mathrm{1}.\mathrm{471654}{h}\:\left({exact}\:{value}\:{possible}\right) \\ $$$${b}_{\mathrm{3}} =\mathrm{6}.\mathrm{903689}{h}\:\left({exact}\:{value}\:{possible}\right) \\ $$$$ \\ $$$${we}\:{see}\:{that}\:{we}\:{can}\:{not}\:{select}\:{the} \\ $$$${point}\:{P},\:{i}.{e}.\:{find}\:{a}\:{value}\:{for}\:{h}\:{such} \\ $$$${that}\:{B}_{\mathrm{1}} \:{coincides}\:{with}\:{B}_{\mathrm{2}} \:{or}\:{B}_{\mathrm{3}} , \\ $$$${that}\:{means}\:{it}'{s}\:{impossible}\:{to}\:{get} \\ $$$${A}_{{I}} ={A}_{{II}} ={A}_{{III}} ={A}_{{IV}} \:. \\ $$
Commented by mr W last updated on 28/Jan/20
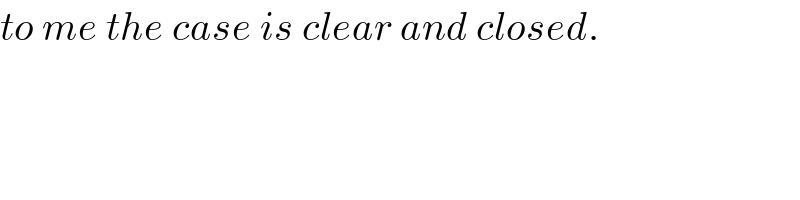
to me the case is clear and closed.
$${to}\:{me}\:{the}\:{case}\:{is}\:{clear}\:{and}\:{closed}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *