Question Number 79731 by M±th+et£s last updated on 27/Jan/20

Commented by M±th+et£s last updated on 27/Jan/20

$${AH}:{HC}=\mathrm{4}:\mathrm{3} \\ $$$${BG}:{GC}=\mathrm{5}:\mathrm{9} \\ $$$${find}\:{AF}:{FB} \\ $$
Commented by mr W last updated on 27/Jan/20
$${equilateral}\:{triangle}? \\ $$
Commented by M±th+et£s last updated on 27/Jan/20

$${yes}\:{sir} \\ $$
Commented by mr W last updated on 27/Jan/20

$$\mathrm{5}:\mathrm{2} \\ $$
Commented by M±th+et£s last updated on 27/Jan/20
$${its}\:{right}\:{but}\:{can}\:{you}\:{show}\:{your}\:{work}\:{and}\:{thank}\:{you}\:{sir} \\ $$
Answered by mr W last updated on 27/Jan/20

Commented by M±th+et£s last updated on 27/Jan/20
$${thank}\:{you}\:{so}\:{much}\:{sir}\: \\ $$
Commented by mr W last updated on 27/Jan/20
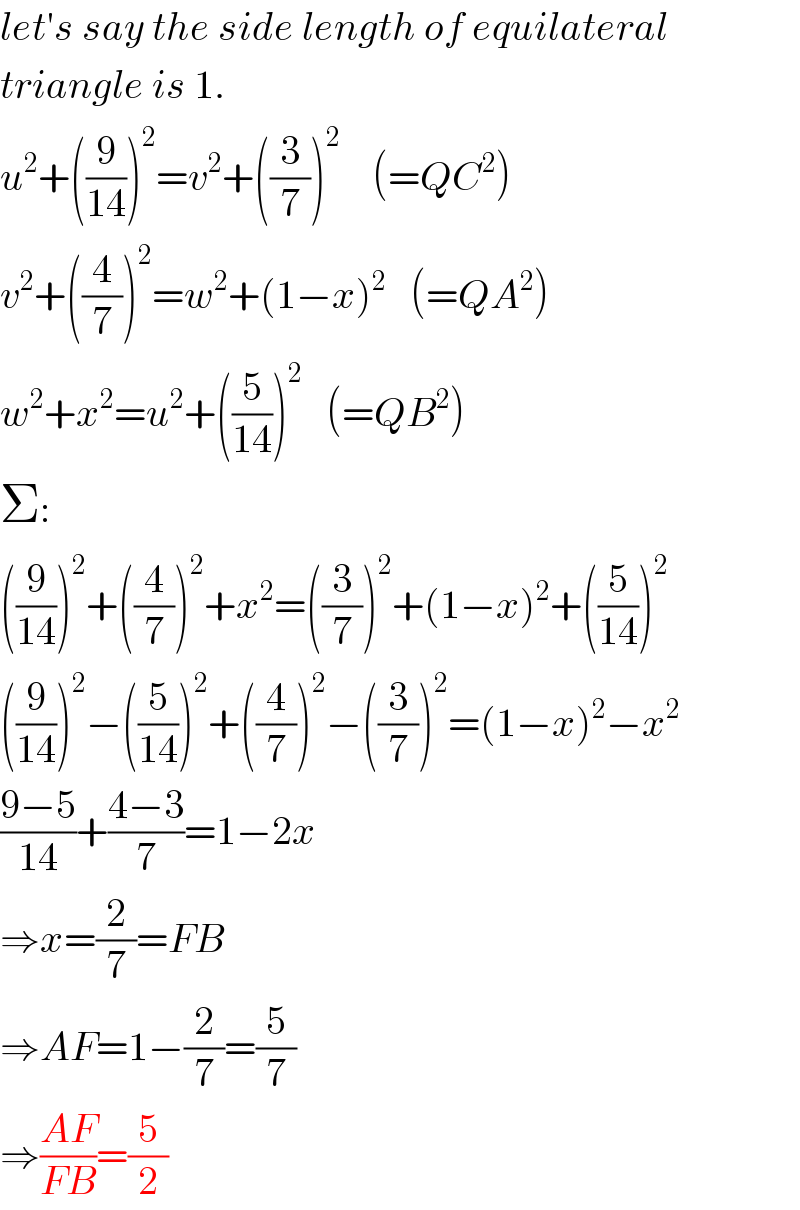
$${let}'{s}\:{say}\:{the}\:{side}\:{length}\:{of}\:{equilateral} \\ $$$${triangle}\:{is}\:\mathrm{1}. \\ $$$${u}^{\mathrm{2}} +\left(\frac{\mathrm{9}}{\mathrm{14}}\right)^{\mathrm{2}} ={v}^{\mathrm{2}} +\left(\frac{\mathrm{3}}{\mathrm{7}}\right)^{\mathrm{2}} \:\:\:\:\left(={QC}^{\mathrm{2}} \right) \\ $$$${v}^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{7}}\right)^{\mathrm{2}} ={w}^{\mathrm{2}} +\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \:\:\:\left(={QA}^{\mathrm{2}} \right) \\ $$$${w}^{\mathrm{2}} +{x}^{\mathrm{2}} ={u}^{\mathrm{2}} +\left(\frac{\mathrm{5}}{\mathrm{14}}\right)^{\mathrm{2}} \:\:\:\left(={QB}^{\mathrm{2}} \right) \\ $$$$\Sigma: \\ $$$$\left(\frac{\mathrm{9}}{\mathrm{14}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{7}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} =\left(\frac{\mathrm{3}}{\mathrm{7}}\right)^{\mathrm{2}} +\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +\left(\frac{\mathrm{5}}{\mathrm{14}}\right)^{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{9}}{\mathrm{14}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{5}}{\mathrm{14}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{7}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}}{\mathrm{7}}\right)^{\mathrm{2}} =\left(\mathrm{1}−{x}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} \\ $$$$\frac{\mathrm{9}−\mathrm{5}}{\mathrm{14}}+\frac{\mathrm{4}−\mathrm{3}}{\mathrm{7}}=\mathrm{1}−\mathrm{2}{x} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}}{\mathrm{7}}={FB} \\ $$$$\Rightarrow{AF}=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{7}}=\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\Rightarrow\frac{{AF}}{{FB}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$
