Question Number 79798 by ajfour last updated on 28/Jan/20
Commented by ajfour last updated on 28/Jan/20
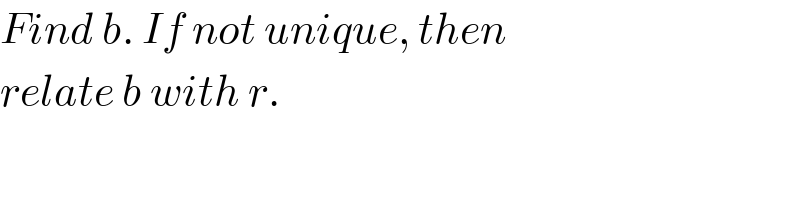
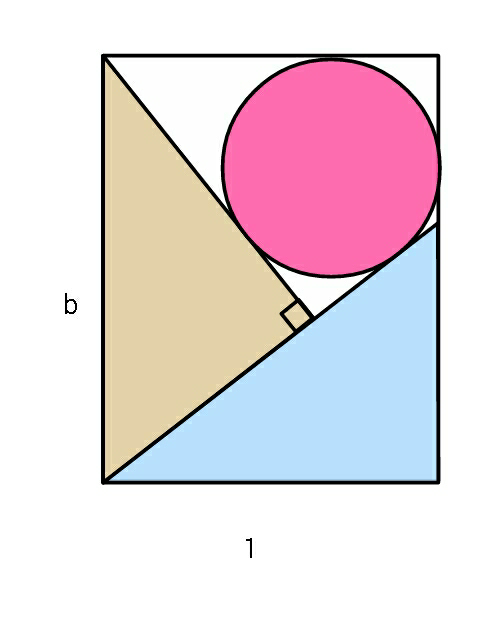
$${Find}\:{b}.\:{If}\:{not}\:{unique},\:{then} \\ $$$${relate}\:{b}\:{with}\:{r}. \\ $$
Commented by key of knowledge last updated on 28/Jan/20

$$\mathrm{i}\:\mathrm{thinks}\:\mathrm{not}\:\mathrm{enouth}\:\mathrm{informaion}. \\ $$$$\mathrm{if}\:\mathrm{R}_{\mathrm{c}} =\mathrm{r}\Rightarrow\mathrm{b}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{r}}{\mathrm{1}−\mathrm{r}}+\frac{\mathrm{1}−\mathrm{r}}{\mathrm{r}}\right) \\ $$
Commented by ajfour last updated on 28/Jan/20
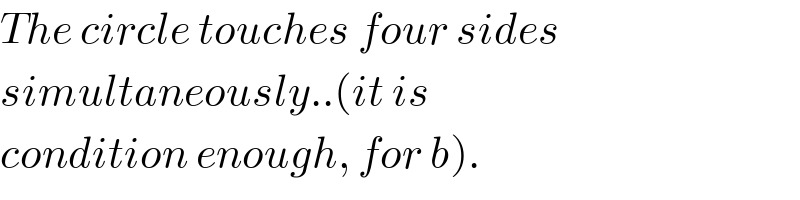
$${The}\:{circle}\:{touches}\:{four}\:{sides} \\ $$$${simultaneously}..\left({it}\:{is}\:\right. \\ $$$$\left.{condition}\:{enough},\:{for}\:{b}\right). \\ $$
Commented by mr W last updated on 28/Jan/20
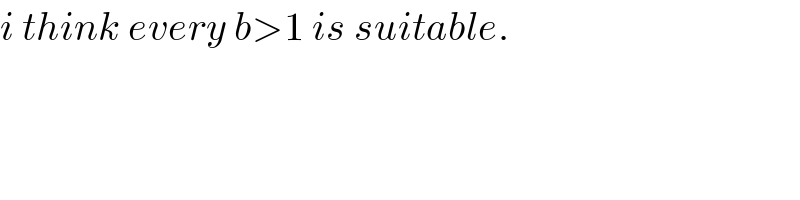
$${i}\:{think}\:{every}\:{b}>\mathrm{1}\:{is}\:{suitable}. \\ $$
Commented by ajfour last updated on 28/Jan/20
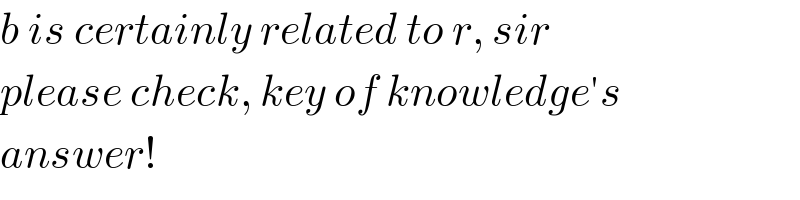
$${b}\:{is}\:{certainly}\:{related}\:{to}\:{r},\:{sir} \\ $$$${please}\:{check},\:{key}\:{of}\:{knowledge}'{s} \\ $$$${answer}! \\ $$
Commented by mr W last updated on 28/Jan/20
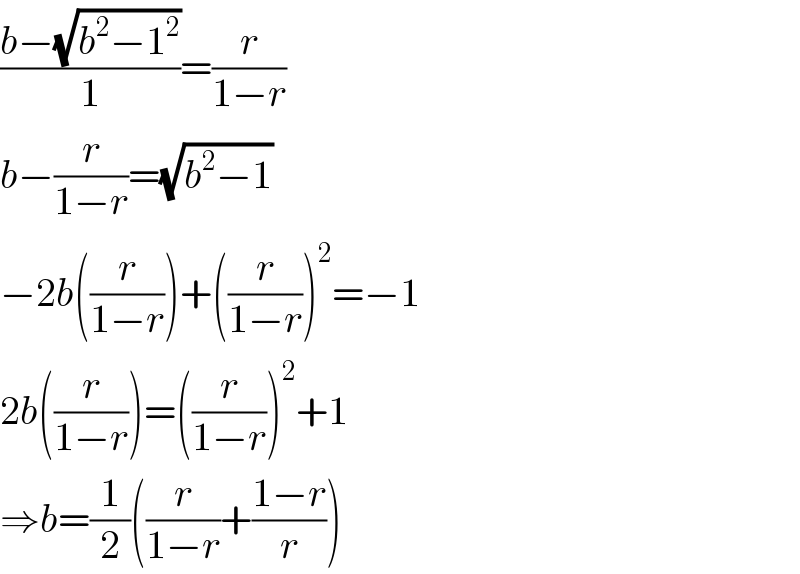
$$\frac{{b}−\sqrt{{b}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }}{\mathrm{1}}=\frac{{r}}{\mathrm{1}−{r}} \\ $$$${b}−\frac{{r}}{\mathrm{1}−{r}}=\sqrt{{b}^{\mathrm{2}} −\mathrm{1}} \\ $$$$−\mathrm{2}{b}\left(\frac{{r}}{\mathrm{1}−{r}}\right)+\left(\frac{{r}}{\mathrm{1}−{r}}\right)^{\mathrm{2}} =−\mathrm{1} \\ $$$$\mathrm{2}{b}\left(\frac{{r}}{\mathrm{1}−{r}}\right)=\left(\frac{{r}}{\mathrm{1}−{r}}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$$\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{r}}{\mathrm{1}−{r}}+\frac{\mathrm{1}−{r}}{{r}}\right) \\ $$
Commented by ajfour last updated on 28/Jan/20
$${Thanks}\:{mrW}\:{Sir}. \\ $$
