Question-79807

Question Number 79807 by Pratah last updated on 28/Jan/20

Commented by Pratah last updated on 28/Jan/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Commented by john santu last updated on 28/Jan/20

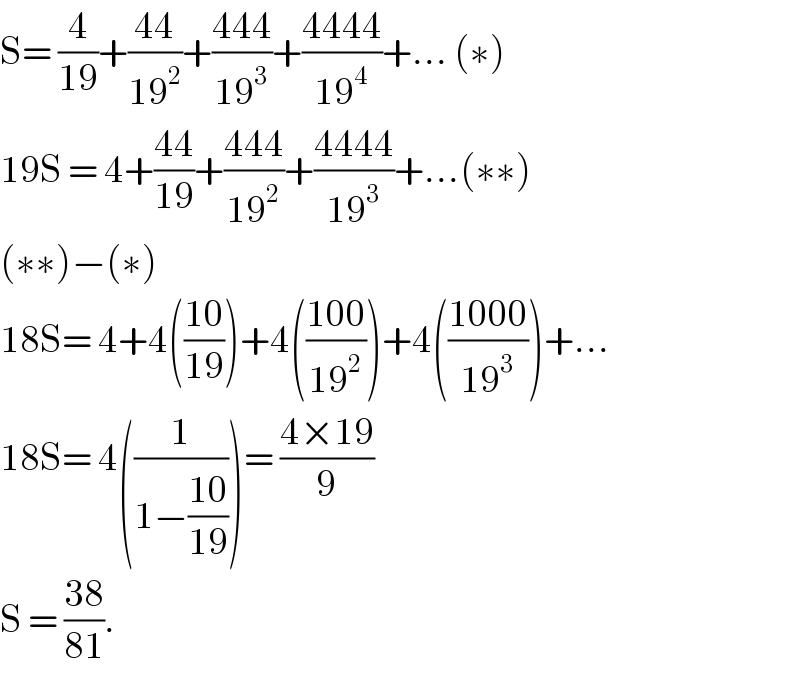
S= (4/(19))+((44)/(19^2 ))+((444)/(19^3 ))+((4444)/(19^4 ))+... (∗) 19S = 4+((44)/(19))+((444)/(19^2 ))+((4444)/(19^3 ))+...(∗∗) (∗∗)−(∗) 18S= 4+4(((10)/(19)))+4(((100)/(19^2 )))+4(((1000)/(19^3 )))+... 18S= 4((1/(1−((10)/(19)))))= ((4×19)/9) S = ((38)/(81)).

$$\mathrm{S}=\:\frac{\mathrm{4}}{\mathrm{19}}+\frac{\mathrm{44}}{\mathrm{19}^{\mathrm{2}} }+\frac{\mathrm{444}}{\mathrm{19}^{\mathrm{3}} }+\frac{\mathrm{4444}}{\mathrm{19}^{\mathrm{4}} }+…\:\left(\ast\right) \\ $$$$\mathrm{19S}\:=\:\mathrm{4}+\frac{\mathrm{44}}{\mathrm{19}}+\frac{\mathrm{444}}{\mathrm{19}^{\mathrm{2}} }+\frac{\mathrm{4444}}{\mathrm{19}^{\mathrm{3}} }+…\left(\ast\ast\right) \\ $$$$\left(\ast\ast\right)−\left(\ast\right) \\ $$$$\mathrm{18S}=\:\mathrm{4}+\mathrm{4}\left(\frac{\mathrm{10}}{\mathrm{19}}\right)+\mathrm{4}\left(\frac{\mathrm{100}}{\mathrm{19}^{\mathrm{2}} }\right)+\mathrm{4}\left(\frac{\mathrm{1000}}{\mathrm{19}^{\mathrm{3}} }\right)+… \\ $$$$\mathrm{18S}=\:\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{10}}{\mathrm{19}}}\right)=\:\frac{\mathrm{4}×\mathrm{19}}{\mathrm{9}} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{38}}{\mathrm{81}}.\: \\ $$

Answered by mr W last updated on 28/Jan/20

S=Σ_(n=1) ^∞ ((4(1+10+100+...+10^(n−1) ))/(19^n )) S=Σ_(n=1) ^∞ ((4(10^n −1))/(9×19^n )) S=(4/9)Σ_(n=1) ^∞ ((10^n −1)/(19^n )) S=(4/9)Σ_(n=1) ^∞ [(((10)/(19)))^n −((1/(19)))^n ] S=(4/9)((((10)/(19))/(1−((10)/(19))))−((1/(19))/(1−(1/(19))))) S=(4/9)(((10)/9)−(1/(18))) ⇒S=((38)/(81))

$${S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}\left(\mathrm{1}+\mathrm{10}+\mathrm{100}+…+\mathrm{10}^{{n}−\mathrm{1}} \right)}{\mathrm{19}^{{n}} } \\ $$$${S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{9}×\mathrm{19}^{{n}} } \\ $$$${S}=\frac{\mathrm{4}}{\mathrm{9}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{10}^{{n}} −\mathrm{1}}{\mathrm{19}^{{n}} } \\ $$$${S}=\frac{\mathrm{4}}{\mathrm{9}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\left(\frac{\mathrm{10}}{\mathrm{19}}\right)^{{n}} −\left(\frac{\mathrm{1}}{\mathrm{19}}\right)^{{n}} \right] \\ $$$${S}=\frac{\mathrm{4}}{\mathrm{9}}\left(\frac{\frac{\mathrm{10}}{\mathrm{19}}}{\mathrm{1}−\frac{\mathrm{10}}{\mathrm{19}}}−\frac{\frac{\mathrm{1}}{\mathrm{19}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{19}}}\right) \\ $$$${S}=\frac{\mathrm{4}}{\mathrm{9}}\left(\frac{\mathrm{10}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{18}}\right) \\ $$$$\Rightarrow{S}=\frac{\mathrm{38}}{\mathrm{81}} \\ $$

Commented by Pratah last updated on 28/Jan/20

$$\mathrm{thanks} \\ $$

Answered by Smail last updated on 28/Jan/20

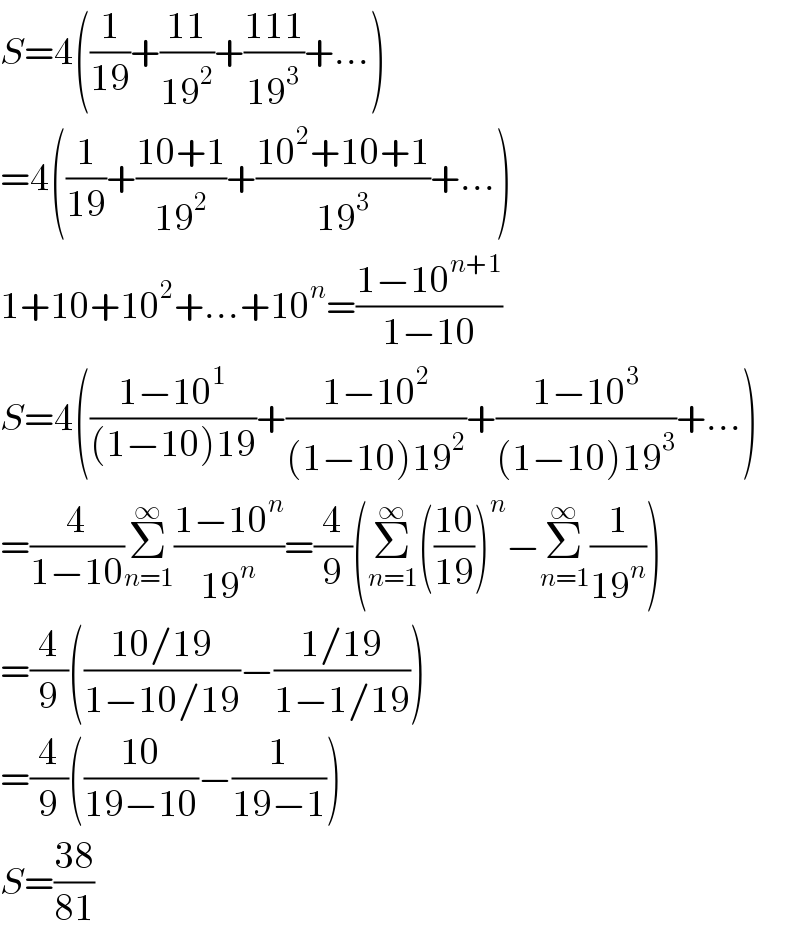
S=4((1/(19))+((11)/(19^2 ))+((111)/(19^3 ))+...) =4((1/(19))+((10+1)/(19^2 ))+((10^2 +10+1)/(19^3 ))+...) 1+10+10^2 +...+10^n =((1−10^(n+1) )/(1−10)) S=4(((1−10^1 )/((1−10)19))+((1−10^2 )/((1−10)19^2 ))+((1−10^3 )/((1−10)19^3 ))+...) =(4/(1−10))Σ_(n=1) ^∞ ((1−10^n )/(19^n ))=(4/9)(Σ_(n=1) ^∞ (((10)/(19)))^n −Σ_(n=1) ^∞ (1/(19^n ))) =(4/9)(((10/19)/(1−10/19))−((1/19)/(1−1/19))) =(4/9)(((10)/(19−10))−(1/(19−1))) S=((38)/(81))

$${S}=\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{19}}+\frac{\mathrm{11}}{\mathrm{19}^{\mathrm{2}} }+\frac{\mathrm{111}}{\mathrm{19}^{\mathrm{3}} }+…\right) \\ $$$$=\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{19}}+\frac{\mathrm{10}+\mathrm{1}}{\mathrm{19}^{\mathrm{2}} }+\frac{\mathrm{10}^{\mathrm{2}} +\mathrm{10}+\mathrm{1}}{\mathrm{19}^{\mathrm{3}} }+…\right) \\ $$$$\mathrm{1}+\mathrm{10}+\mathrm{10}^{\mathrm{2}} +…+\mathrm{10}^{{n}} =\frac{\mathrm{1}−\mathrm{10}^{{n}+\mathrm{1}} }{\mathrm{1}−\mathrm{10}} \\ $$$${S}=\mathrm{4}\left(\frac{\mathrm{1}−\mathrm{10}^{\mathrm{1}} }{\left(\mathrm{1}−\mathrm{10}\right)\mathrm{19}}+\frac{\mathrm{1}−\mathrm{10}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{10}\right)\mathrm{19}^{\mathrm{2}} }+\frac{\mathrm{1}−\mathrm{10}^{\mathrm{3}} }{\left(\mathrm{1}−\mathrm{10}\right)\mathrm{19}^{\mathrm{3}} }+…\right) \\ $$$$=\frac{\mathrm{4}}{\mathrm{1}−\mathrm{10}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}−\mathrm{10}^{{n}} }{\mathrm{19}^{{n}} }=\frac{\mathrm{4}}{\mathrm{9}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{10}}{\mathrm{19}}\right)^{{n}} −\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{19}^{{n}} }\right) \\ $$$$=\frac{\mathrm{4}}{\mathrm{9}}\left(\frac{\mathrm{10}/\mathrm{19}}{\mathrm{1}−\mathrm{10}/\mathrm{19}}−\frac{\mathrm{1}/\mathrm{19}}{\mathrm{1}−\mathrm{1}/\mathrm{19}}\right) \\ $$$$=\frac{\mathrm{4}}{\mathrm{9}}\left(\frac{\mathrm{10}}{\mathrm{19}−\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{19}−\mathrm{1}}\right) \\ $$$${S}=\frac{\mathrm{38}}{\mathrm{81}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply