Question-79824

Question Number 79824 by TawaTawa last updated on 28/Jan/20

Commented by TawaTawa last updated on 28/Jan/20

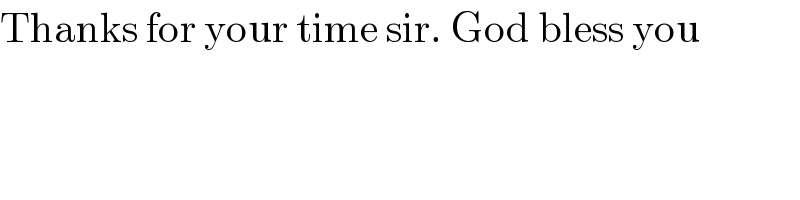
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$

Commented by TawaTawa last updated on 28/Jan/20

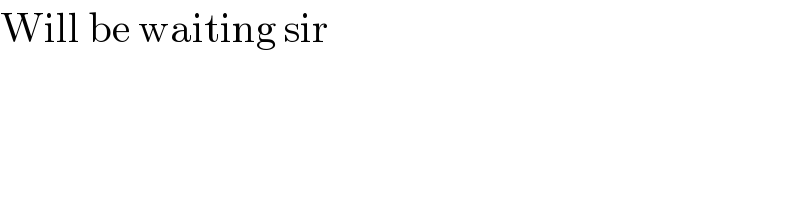
$$\mathrm{Will}\:\mathrm{be}\:\mathrm{waiting}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 29/Jan/20

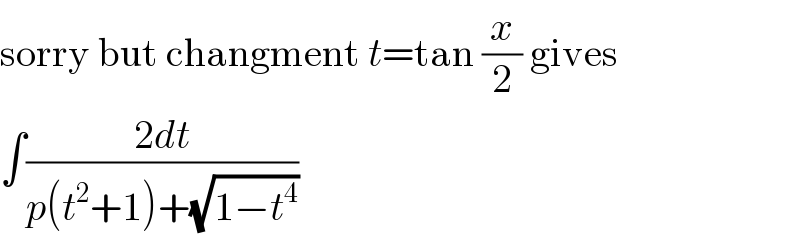
sorry but changment t=tan (x/2) gives ∫((2dt)/(p(t^2 +1)+(√(1−t^4 ))))

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{changment}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\mathrm{gives} \\ $$$$\int\frac{\mathrm{2}{dt}}{{p}\left({t}^{\mathrm{2}} +\mathrm{1}\right)+\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }} \\ $$

Commented by mind is power last updated on 29/Jan/20

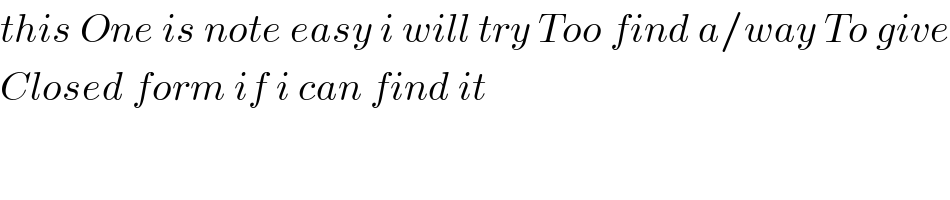
$${this}\:{One}\:{is}\:{note}\:{easy}\:{i}\:{will}\:{try}\:{Too}\:{find}\:{a}/{way}\:{To}\:{give} \\ $$$${Closed}\:{form}\:{if}\:{i}\:{can}\:{find}\:{it} \\ $$

Commented by mathmax by abdo last updated on 29/Jan/20

let take a try A =∫_0 ^(π/2) (dx/(p+(√(cosx)))) cha7gement tan((x/2))=t give A =∫_0 ^1 (1/(p+(√((1−t^2 )/(1+t^2 )))))×(2/(1+t^2 ))dt =2 ∫_0 ^1 (dt/(p(1+t^2 )+(√(1−t^4 )))) =2 ∫_0 ^1 ((p(1+t^2 )−(√(1−t^4 )))/(p^2 (1+t^2 )^2 −(1−t^4 )))dt =2p ∫_0 ^1 ((t^2 +1)/(p^2 (t^4 +2t^2 +1)−1+t^4 ))dt −2 ∫_0 ^1 ((√(1−t^4 ))/(p^2 (t^4 +2t^2 +1)−1+t^4 ))dt =2p ∫_0 ^1 ((t^2 +1)/((p^2 +1)t^4 +2p^2 t^2 +p^2 −1))dt −2 ∫_0 ^1 ((√(1−t^4 ))/((p^2 +1)t^4 +2p^2 t^2 +p^2 −1))dt =A−B let decompose F(t) =((t^2 +1)/((p^(2 ) +1)t^4 +2p^2 t^2 +p^2 −1)) =((x+1)/((p^2 +1)x^2 +2p^2 x +p^2 −1))=g(x) with x=t^2 Δ^′ =p^4 −(p^4 −1) =1 ⇒x_1 =((−p^2 +1)/(p^2 +1)) =((1−p^2 )/(1+p^2 )) x_2 =((−p^2 −1)/(p^2 +1)) =−1 ⇒g(x)=((x+1)/((p^2 +1)(x+1)(x−((1−p^2 )/(1+p^2 ))))) =(1/((p^2 +1)(x−((1−p^2 )/(1+p^2 ))))) =(1/((p^2 +1)(t^2 −((1−p^2 )/(1+p^2 ))))) if p>1 we get F(t) =(1/((p^2 +1)(t^2 +((p^2 −1)/(p^2 +1))))) we do the changement t=(√((p^2 −1)/(p^2 +1)))u ⇒2p∫_0 ^1 F(t)dt =((2p)/(p^2 +1)) ∫_0 ^(√((p^2 +1)/(p^2 −1))) (1/(u^2 +1))×((p^2 +1)/(p^2 −1))du =((2p)/(p^2 −1)) arctan(√((p^2 +1)/(p^2 −1))) if 0<p<1 we get F(t)=(1/((p^2 +1)(t−a_p )(t+a_p ))) (a_p =(√((1−p^2 )/(1+p^2 ))))=(1/(2a_p (p^2 +1))){(1/(t−a_p ))−(1/(t+a_p ))} ⇒ 2p ∫_0 ^1 F(t)dt =(p/(a_p (p^2 +1))) [ln∣((t−a_p )/(t+a_p ))∣]_0 ^1 =(p/(a_p (p^2 +1)))ln∣((1−a_p )/(1+a_p ))∣ ...be continued...

$${let}\:{take}\:{a}\:{try}\:\:\:{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{{p}+\sqrt{{cosx}}}\:\:{cha}\mathrm{7}{gement}\:\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{{p}+\sqrt{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}}×\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{{p}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{p}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)−\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}{{p}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{1}−{t}^{\mathrm{4}} \right)}{dt}\:=\mathrm{2}{p}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{p}^{\mathrm{2}} \left({t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\right)−\mathrm{1}+{t}^{\mathrm{4}} }{dt} \\ $$$$−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}{{p}^{\mathrm{2}} \left({t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\right)−\mathrm{1}+{t}^{\mathrm{4}} }{dt} \\ $$$$=\mathrm{2}{p}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{\left({p}^{\mathrm{2}} \:+\mathrm{1}\right){t}^{\mathrm{4}} \:+\mathrm{2}{p}^{\mathrm{2}} {t}^{\mathrm{2}} \:+{p}^{\mathrm{2}} \:−\mathrm{1}}{dt}\:−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}{\left({p}^{\mathrm{2}} \:+\mathrm{1}\right){t}^{\mathrm{4}} \:+\mathrm{2}{p}^{\mathrm{2}} {t}^{\mathrm{2}} \:+{p}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$={A}−{B}\:\:{let}\:{decompose}\:{F}\left({t}\right)\:=\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{\left({p}^{\mathrm{2}\:} +\mathrm{1}\right){t}^{\mathrm{4}} \:+\mathrm{2}{p}^{\mathrm{2}} {t}^{\mathrm{2}} \:+{p}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{{x}+\mathrm{1}}{\left({p}^{\mathrm{2}} \:+\mathrm{1}\right){x}^{\mathrm{2}} \:+\mathrm{2}{p}^{\mathrm{2}} {x}\:+{p}^{\mathrm{2}} −\mathrm{1}}={g}\left({x}\right)\:\:{with}\:{x}={t}^{\mathrm{2}} \\ $$$$\Delta^{'} \:={p}^{\mathrm{4}} −\left({p}^{\mathrm{4}} −\mathrm{1}\right)\:=\mathrm{1}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−{p}^{\mathrm{2}} \:+\mathrm{1}}{{p}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{1}−{p}^{\mathrm{2}} }{\mathrm{1}+{p}^{\mathrm{2}} } \\ $$$${x}_{\mathrm{2}} =\frac{−{p}^{\mathrm{2}} \:−\mathrm{1}}{{p}^{\mathrm{2}} \:+\mathrm{1}}\:=−\mathrm{1}\:\Rightarrow{g}\left({x}\right)=\frac{{x}+\mathrm{1}}{\left({p}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}+\mathrm{1}\right)\left({x}−\frac{\mathrm{1}−{p}^{\mathrm{2}} }{\mathrm{1}+{p}^{\mathrm{2}} }\right)} \\ $$$$=\frac{\mathrm{1}}{\left({p}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}−\frac{\mathrm{1}−{p}^{\mathrm{2}} }{\mathrm{1}+{p}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{1}}{\left({p}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{2}} −\frac{\mathrm{1}−{p}^{\mathrm{2}} }{\mathrm{1}+{p}^{\mathrm{2}} }\right)} \\ $$$${if}\:\:{p}>\mathrm{1}\:\:{we}\:{get}\:\:{F}\left({t}\right)\:=\frac{\mathrm{1}}{\left({p}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\frac{{p}^{\mathrm{2}} −\mathrm{1}}{{p}^{\mathrm{2}} \:+\mathrm{1}}\right)}\:\:{we}\:{do}\:{the}\:{changement} \\ $$$${t}=\sqrt{\frac{{p}^{\mathrm{2}} −\mathrm{1}}{{p}^{\mathrm{2}} +\mathrm{1}}}{u}\:\Rightarrow\mathrm{2}{p}\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({t}\right){dt}\:=\frac{\mathrm{2}{p}}{{p}^{\mathrm{2}} \:+\mathrm{1}}\:\int_{\mathrm{0}} ^{\sqrt{\frac{{p}^{\mathrm{2}} +\mathrm{1}}{{p}^{\mathrm{2}} −\mathrm{1}}}} \:\:\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{1}}×\frac{{p}^{\mathrm{2}} +\mathrm{1}}{{p}^{\mathrm{2}} −\mathrm{1}}{du} \\ $$$$=\frac{\mathrm{2}{p}}{{p}^{\mathrm{2}} −\mathrm{1}}\:{arctan}\sqrt{\frac{{p}^{\mathrm{2}} +\mathrm{1}}{{p}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${if}\:\mathrm{0}<{p}<\mathrm{1}\:{we}\:{get}\:{F}\left({t}\right)=\frac{\mathrm{1}}{\left({p}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}−{a}_{{p}} \right)\left({t}+{a}_{{p}} \right)} \\ $$$$\left({a}_{{p}} =\sqrt{\frac{\mathrm{1}−{p}^{\mathrm{2}} }{\mathrm{1}+{p}^{\mathrm{2}} }}\right)=\frac{\mathrm{1}}{\mathrm{2}{a}_{{p}} \left({p}^{\mathrm{2}} \:+\mathrm{1}\right)}\left\{\frac{\mathrm{1}}{{t}−{a}_{{p}} }−\frac{\mathrm{1}}{{t}+{a}_{{p}} }\right\}\:\Rightarrow \\ $$$$\mathrm{2}{p}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({t}\right){dt}\:=\frac{{p}}{{a}_{{p}} \left({p}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\left[{ln}\mid\frac{{t}−{a}_{{p}} }{{t}+{a}_{{p}} }\mid\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{{p}}{{a}_{{p}} \left({p}^{\mathrm{2}} \:+\mathrm{1}\right)}{ln}\mid\frac{\mathrm{1}−{a}_{{p}} }{\mathrm{1}+{a}_{{p}} }\mid \\ $$$$…{be}\:{continued}… \\ $$

Commented by TawaTawa last updated on 30/Jan/20

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by mathmax by abdo last updated on 30/Jan/20

$${you}\:{are}\:{welcome}. \\ $$

Answered by Kamel Kamel last updated on 29/Jan/20

Abdomathmax dx=((2dt)/(1+t^2 )) not ((2dt)/( (√(1+t^2 )))). The closed form of this integral is given with hypergeometric functions.

$$\mathrm{Abdomathmax}\:\mathrm{dx}=\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\mathrm{not}\:\frac{\mathrm{2dt}}{\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}. \\ $$$$\mathrm{The}\:\mathrm{closed}\:\mathrm{form}\:\mathrm{of}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{is} \\ $$$$\mathrm{given}\:\mathrm{with}\:\mathrm{hypergeometric}\:\mathrm{functions}. \\ $$

Answered by mind is power last updated on 30/Jan/20