Question Number 79826 by Pratah last updated on 28/Jan/20
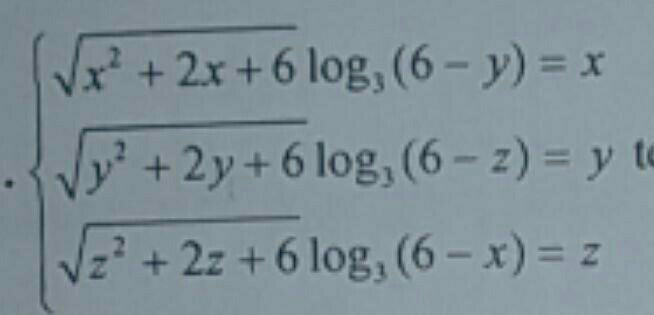
Commented by Pratah last updated on 28/Jan/20

$$\mathrm{please}\:\:\mathrm{solution}.\:\:\mathrm{help} \\ $$
Commented by mr W last updated on 28/Jan/20

$${you}\:{may}\:{repeat}\:{the}\:{question}\:{another} \\ $$$$\infty\:{times},\:{but}\:{you}\:{won}'{t}\:{get}\:{an}\:{other} \\ $$$${answer}\:{than}\:{in}\:{Q}\mathrm{78732}… \\ $$
Commented by Pratah last updated on 28/Jan/20

$$\mathrm{solution}\:\mathrm{pls} \\ $$
Commented by mr W last updated on 28/Jan/20
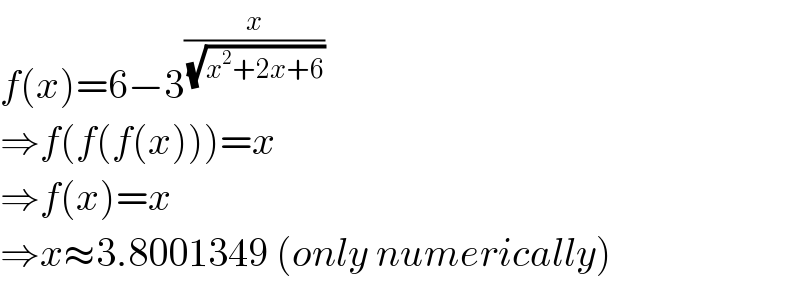
$${f}\left({x}\right)=\mathrm{6}−\mathrm{3}^{\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{6}}}} \\ $$$$\Rightarrow{f}\left({f}\left({f}\left({x}\right)\right)\right)={x} \\ $$$$\Rightarrow{f}\left({x}\right)={x} \\ $$$$\Rightarrow{x}\approx\mathrm{3}.\mathrm{8001349}\:\left({only}\:{numerically}\right) \\ $$
Commented by Pratah last updated on 28/Jan/20
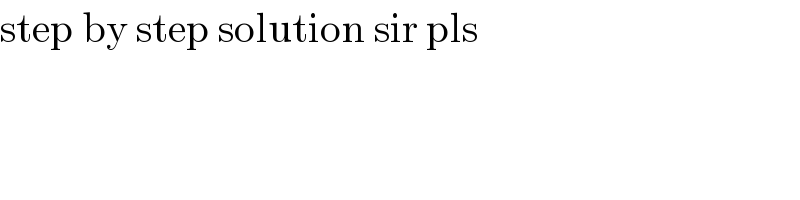
$$\mathrm{step}\:\mathrm{by}\:\mathrm{step}\:\mathrm{solution}\:\mathrm{sir}\:\mathrm{pls} \\ $$
Commented by mr W last updated on 28/Jan/20
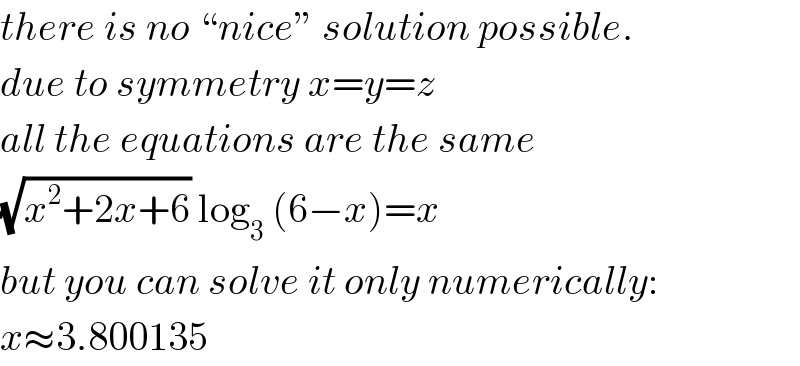
$${there}\:{is}\:{no}\:“{nice}''\:{solution}\:{possible}. \\ $$$${due}\:{to}\:{symmetry}\:{x}={y}={z} \\ $$$${all}\:{the}\:{equations}\:{are}\:{the}\:{same} \\ $$$$\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{6}}\:\mathrm{log}_{\mathrm{3}} \:\left(\mathrm{6}−{x}\right)={x} \\ $$$${but}\:{you}\:{can}\:{solve}\:{it}\:{only}\:{numerically}: \\ $$$${x}\approx\mathrm{3}.\mathrm{800135} \\ $$
Commented by Pratah last updated on 28/Jan/20

$$\mathrm{ok} \\ $$
