Question Number 79837 by Pratah last updated on 28/Jan/20
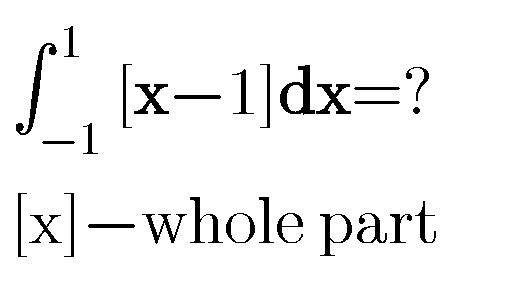
Commented by mr W last updated on 28/Jan/20

$${see}\:{Q}\mathrm{79814} \\ $$
Commented by Pratah last updated on 28/Jan/20

$$\mathrm{this}\:\mathrm{one}\:\mathrm{is}\:\mathrm{different} \\ $$
Commented by mr W last updated on 28/Jan/20

$${if}\:{you}\:{understand}\:{Q}\mathrm{79814},\:{then}\:{you} \\ $$$${should}\:{also}\:{be}\:{able}\:{to}\:{solve}\:{this}\:{one}. \\ $$
Commented by Pratah last updated on 28/Jan/20

$$\mathrm{no} \\ $$
Commented by mr W last updated on 28/Jan/20
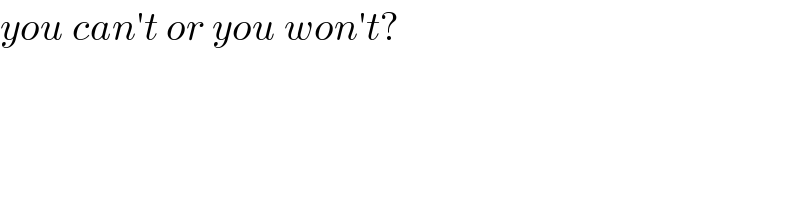
$${you}\:{can}'{t}\:{or}\:{you}\:{won}'{t}? \\ $$
Commented by abdomathmax last updated on 28/Jan/20
![∫_(−1) ^1 [x−1]dx =∫_(−1) ^1 [x]dx −∫_(−1) ^1 dx =∫_(−1) ^0 (−1)dx +∫_0 ^1 )o)dx −2 =1−2 =−1](https://www.tinkutara.com/question/Q79868.png)
$$\int_{−\mathrm{1}} ^{\mathrm{1}} \left[{x}−\mathrm{1}\right]{dx}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \left[{x}\right]{dx}\:−\int_{−\mathrm{1}} ^{\mathrm{1}} {dx} \\ $$$$\left.=\left.\int_{−\mathrm{1}} ^{\mathrm{0}} \left(−\mathrm{1}\right){dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \right){o}\right){dx}\:−\mathrm{2} \\ $$$$=\mathrm{1}−\mathrm{2}\:=−\mathrm{1} \\ $$
Commented by Pratah last updated on 29/Jan/20
$$\mathrm{no}\:\mathrm{correct} \\ $$
Commented by Pratah last updated on 29/Jan/20
$$\mathrm{sir}\:\mathrm{abdomathmax} \\ $$
Commented by mr W last updated on 29/Jan/20
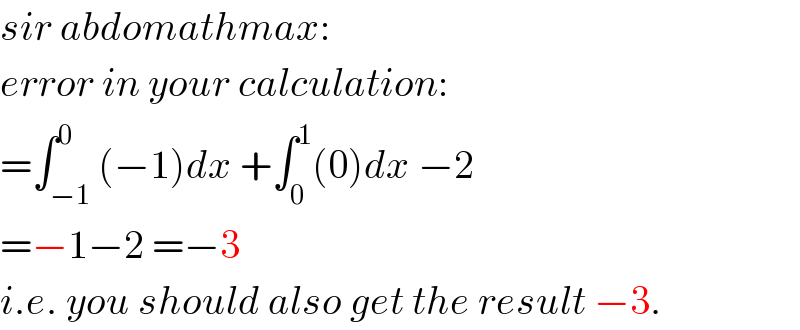
$${sir}\:{abdomathmax}: \\ $$$${error}\:{in}\:{your}\:{calculation}: \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{0}} \left(−\mathrm{1}\right){dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{0}\right){dx}\:−\mathrm{2} \\ $$$$=−\mathrm{1}−\mathrm{2}\:=−\mathrm{3} \\ $$$${i}.{e}.\:{you}\:{should}\:{also}\:{get}\:{the}\:{result}\:−\mathrm{3}. \\ $$
Commented by mathmax by abdo last updated on 29/Jan/20
$${yes}\:{sir}\:{thank}\:{you}. \\ $$
Answered by key of knowledge last updated on 28/Jan/20
![−1≤x<0⇒[x−1]=−2⇒∫_(−1) ^0 (−2)dx=−2 0≤x<1⇒∫_0 ^1 (−1)dx=−1 (−1)+(−2)=−3](https://www.tinkutara.com/question/Q79859.png)
$$−\mathrm{1}\leqslant\mathrm{x}<\mathrm{0}\Rightarrow\left[\mathrm{x}−\mathrm{1}\right]=−\mathrm{2}\Rightarrow\int_{−\mathrm{1}} ^{\mathrm{0}} \left(−\mathrm{2}\right)\mathrm{dx}=−\mathrm{2} \\ $$$$\mathrm{0}\leqslant\mathrm{x}<\mathrm{1}\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)\mathrm{dx}=−\mathrm{1} \\ $$$$\left(−\mathrm{1}\right)+\left(−\mathrm{2}\right)=−\mathrm{3} \\ $$
Commented by Pratah last updated on 28/Jan/20

$$\mathrm{answer}:\:−\mathrm{1} \\ $$
Commented by mr W last updated on 28/Jan/20
![sir Pratah: to understand your definition, please answer: [−0.8]=−1 or 0 ?](https://www.tinkutara.com/question/Q79865.png)
$${sir}\:{Pratah}: \\ $$$${to}\:{understand}\:{your}\:{definition},\:{please} \\ $$$${answer}: \\ $$$$\left[−\mathrm{0}.\mathrm{8}\right]=−\mathrm{1}\:{or}\:\mathrm{0}\:? \\ $$
Commented by MJS last updated on 28/Jan/20
wait... he must answer to understand? ...or he must understand to answer? ����
Commented by Pratah last updated on 29/Jan/20
![[−1+0.2]=−1 ;(](https://www.tinkutara.com/question/Q79901.png)
$$\left[−\mathrm{1}+\mathrm{0}.\mathrm{2}\right]=−\mathrm{1}\:\:;\left(\right. \\ $$
Commented by mr W last updated on 29/Jan/20
![pratah sir: if [−0.8]=−1 then ∫_(−1) ^( 1) [x−1]dx=−3 ≠−1 (which you gave)](https://www.tinkutara.com/question/Q79908.png)
$${pratah}\:{sir}: \\ $$$${if}\:\left[−\mathrm{0}.\mathrm{8}\right]=−\mathrm{1} \\ $$$${then} \\ $$$$\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left[{x}−\mathrm{1}\right]{dx}=−\mathrm{3}\:\neq−\mathrm{1}\:\left({which}\:{you}\:{gave}\right) \\ $$
Commented by Pratah last updated on 29/Jan/20

Commented by mr W last updated on 29/Jan/20
![build your own opinion if you don′t have one! that′s why i asked you the definition of [−0.8] at the begining! you told [−0.8]=−1, but this diagram shows the graph [x−1], and it shows at x=0.5: [0.5−1]=[−0.5]=0≠−1 at x=−0.5: [−0.5−1]=[−1.5]=−1≠−2. that means the solution you gave uses a different definition for [x] than you!](https://www.tinkutara.com/question/Q79927.png)
$${build}\:{your}\:{own}\:{opinion}\:{if}\:{you}\:{don}'{t} \\ $$$${have}\:{one}! \\ $$$${that}'{s}\:{why}\:{i}\:{asked}\:{you}\:{the}\:{definition} \\ $$$${of}\:\left[−\mathrm{0}.\mathrm{8}\right]\:{at}\:{the}\:{begining}! \\ $$$${you}\:{told}\:\left[−\mathrm{0}.\mathrm{8}\right]=−\mathrm{1},\:{but}\:{this}\:{diagram} \\ $$$${shows}\:{the}\:{graph}\:\left[{x}−\mathrm{1}\right],\:{and}\:{it}\:{shows} \\ $$$${at}\:{x}=\mathrm{0}.\mathrm{5}:\:\left[\mathrm{0}.\mathrm{5}−\mathrm{1}\right]=\left[−\mathrm{0}.\mathrm{5}\right]=\mathrm{0}\neq−\mathrm{1} \\ $$$${at}\:{x}=−\mathrm{0}.\mathrm{5}:\:\left[−\mathrm{0}.\mathrm{5}−\mathrm{1}\right]=\left[−\mathrm{1}.\mathrm{5}\right]=−\mathrm{1}\neq−\mathrm{2}. \\ $$$${that}\:{means}\:{the}\:{solution}\:{you}\:{gave} \\ $$$${uses}\:{a}\:{different}\:{definition}\:{for}\:\left[{x}\right] \\ $$$${than}\:{you}! \\ $$
