Menu Close

Question-79932

Tinku Tara 0 Comments
Pin




Question Number 79932 by mr W last updated on 29/Jan/20
Commented by mr W last updated on 29/Jan/20
[Q79861 reposted]
$$\left[{Q}\mathrm{79861}\:{reposted}\right] \\ $$
Answered by mr W last updated on 29/Jan/20
I think I′ve found an easy way to prove: let′s look at f(x)=ln (x), we see f(x)=ln x≤(x/e) (“=” is only at x=e) (see diagram below if you have doubt) P_n =(√(2((3((4...(n)^(1/n) ))^(1/4) ))^(1/3) )) P_n =2^(1/2) 3^((1/2)×(1/3)) 4^((1/2)×(1/3)×(1/4)) ...n^((1/2)×(1/3)×(1/4)×...×(1/n)) P_n =2^(1/(2!)) 3^(1/(3!)) 4^(1/(4!)) ...n^(1/(n!)) =Π_(k=2) ^n k^(1/(k!)) ln P_n =Σ_(k=2) ^n ((ln k)/(k!))<Σ_(k=2) ^n (k/(ek!))=(1/e)Σ_(k=2) ^n (1/((k−1)!))=(1/e)Σ_(k=1) ^(n−1) (1/(k!)) <(1/e)Σ_(k=1) ^∞ (1/(k!))=(1/e)(Σ_(k=0) ^∞ (1/(k!))−1)=(1/e)(e−1)=1−(1/e) ⇒P_n <e^(1−(1/e)) =(e/( (e)^(1/e) ))≈1.8816<2 ⇒proved
$${I}\:{think}\:{I}'{ve}\:{found}\:{an}\:{easy}\:{way}\:{to}\:{prove}: \\ $$$$ \\ $$$${let}'{s}\:{look}\:{at}\:{f}\left({x}\right)=\mathrm{ln}\:\left({x}\right),\:{we}\:{see} \\ $$$${f}\left({x}\right)=\mathrm{ln}\:{x}\leqslant\frac{{x}}{{e}}\:\left(“=''\:{is}\:{only}\:{at}\:{x}={e}\right) \\ $$$$\left({see}\:{diagram}\:{below}\:{if}\:{you}\:{have}\:{doubt}\right) \\ $$$$ \\ $$$${P}_{{n}} =\sqrt{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt[{\mathrm{4}}]{\mathrm{4}…\sqrt[{{n}}]{{n}}}}} \\ $$$${P}_{{n}} =\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{4}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}} …{n}^{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}×…×\frac{\mathrm{1}}{{n}}} \\ $$$${P}_{{n}} =\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}!}} \mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}!}} \mathrm{4}^{\frac{\mathrm{1}}{\mathrm{4}!}} …{n}^{\frac{\mathrm{1}}{{n}!}} =\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}{k}^{\frac{\mathrm{1}}{{k}!}} \\ $$$$\mathrm{ln}\:{P}_{{n}} =\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\frac{\mathrm{ln}\:{k}}{{k}!}<\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\:\frac{{k}}{{ek}!}=\frac{\mathrm{1}}{{e}}\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!}=\frac{\mathrm{1}}{{e}}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{k}!} \\ $$$$<\frac{\mathrm{1}}{{e}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}=\frac{\mathrm{1}}{{e}}\left(\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}!}−\mathrm{1}\right)=\frac{\mathrm{1}}{{e}}\left({e}−\mathrm{1}\right)=\mathrm{1}−\frac{\mathrm{1}}{{e}} \\ $$$$\Rightarrow{P}_{{n}} <{e}^{\mathrm{1}−\frac{\mathrm{1}}{{e}}} =\frac{{e}}{\:\sqrt[{{e}}]{{e}}}\approx\mathrm{1}.\mathrm{8816}<\mathrm{2}\:\Rightarrow{proved} \\ $$
Commented by M±th+et£s last updated on 29/Jan/20
thank you sir great solution
$${thank}\:{you}\:{sir}\:{great}\:{solution} \\ $$
Commented by MJS last updated on 29/Jan/20
lim_(n→∞) P_n ≈1.82902467956
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{P}_{{n}} \:\approx\mathrm{1}.\mathrm{82902467956} \\ $$
Commented by MJS last updated on 29/Jan/20
P_n =2^(1/(2!)) 3^(1/(3!)) 4^(1/(4!)) ...n^(1/(n!)) looking at the prime factors... 2^(1/(2!)) 3^(1/(3!)) 4^(1/(4!)) 5^(1/(5!)) 6^(1/(6!)) 7^(1/(7!)) 8^(1/(8!)) 9^(1/(9!)) 10^(1/(10!)) = =2^((2122111)/(3628800)) 3^((20329)/(120960)) 5^((30241)/(3628800)) 7^(1/(5040)) this looks nasty... we should hope for another Riemann...
$${P}_{{n}} =\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}!}} \mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}!}} \mathrm{4}^{\frac{\mathrm{1}}{\mathrm{4}!}} …{n}^{\frac{\mathrm{1}}{{n}!}} \\ $$$$\mathrm{looking}\:\mathrm{at}\:\mathrm{the}\:\mathrm{prime}\:\mathrm{factors}… \\ $$$$\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}!}} \mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}!}} \mathrm{4}^{\frac{\mathrm{1}}{\mathrm{4}!}} \mathrm{5}^{\frac{\mathrm{1}}{\mathrm{5}!}} \mathrm{6}^{\frac{\mathrm{1}}{\mathrm{6}!}} \mathrm{7}^{\frac{\mathrm{1}}{\mathrm{7}!}} \mathrm{8}^{\frac{\mathrm{1}}{\mathrm{8}!}} \mathrm{9}^{\frac{\mathrm{1}}{\mathrm{9}!}} \mathrm{10}^{\frac{\mathrm{1}}{\mathrm{10}!}} = \\ $$$$=\mathrm{2}^{\frac{\mathrm{2122111}}{\mathrm{3628800}}} \mathrm{3}^{\frac{\mathrm{20329}}{\mathrm{120960}}} \mathrm{5}^{\frac{\mathrm{30241}}{\mathrm{3628800}}} \mathrm{7}^{\frac{\mathrm{1}}{\mathrm{5040}}} \\ $$$$\mathrm{this}\:\mathrm{looks}\:\mathrm{nasty}…\:\mathrm{we}\:\mathrm{should}\:\mathrm{hope}\:\mathrm{for}\:\mathrm{another} \\ $$$$\mathrm{Riemann}… \\ $$
Commented by TawaTawa last updated on 29/Jan/20
Sir mrW, come and help me in Q79943
$$\mathrm{Sir}\:\mathrm{mrW},\:\mathrm{come}\:\mathrm{and}\:\mathrm{help}\:\mathrm{me}\:\mathrm{in}\:\:\mathrm{Q79943} \\ $$
Commented by mr W last updated on 29/Jan/20
Commented by mr W last updated on 29/Jan/20
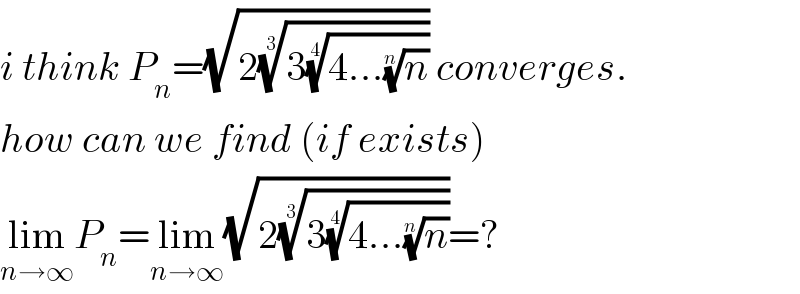
i think P_n =(√(2((3((4...(n)^(1/n) ))^(1/4) ))^(1/3) )) converges. how can we find (if exists) lim_(n→∞) P_n =lim_(n→∞) (√(2((3((4...(n)^(1/n) ))^(1/4) ))^(1/3) ))=?
$${i}\:{think}\:{P}_{{n}} =\sqrt{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt[{\mathrm{4}}]{\mathrm{4}…\sqrt[{{n}}]{{n}}}}}\:{converges}. \\ $$$${how}\:{can}\:{we}\:{find}\:\left({if}\:{exists}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{P}_{{n}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{3}\sqrt[{\mathrm{4}}]{\mathrm{4}…\sqrt[{{n}}]{{n}}}}}=? \\ $$
Commented by mr W last updated on 29/Jan/20
thanks sir! is any “exact” solution possible?
$${thanks}\:{sir}! \\ $$$${is}\:{any}\:“{exact}''\:{solution}\:{possible}? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *