Question Number 79966 by M±th+et£s last updated on 29/Jan/20

Commented by M±th+et£s last updated on 29/Jan/20

$${solve}\:{thd}\:{ODE} \\ $$
Answered by mr W last updated on 29/Jan/20
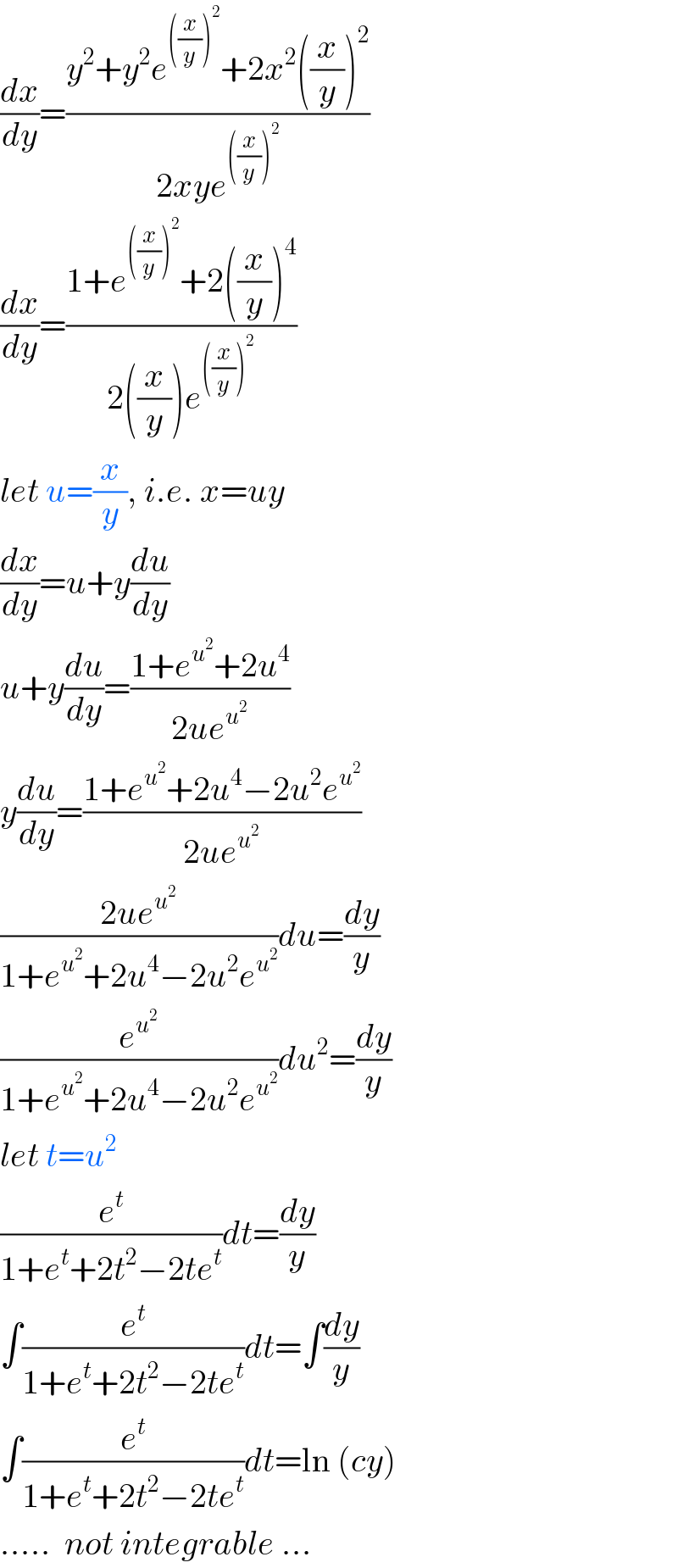
$$\frac{{dx}}{{dy}}=\frac{{y}^{\mathrm{2}} +{y}^{\mathrm{2}} {e}^{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} } +\mathrm{2}{x}^{\mathrm{2}} \left(\frac{{x}}{{y}}\right)^{\mathrm{2}} }{\mathrm{2}{xye}^{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} } } \\ $$$$\frac{{dx}}{{dy}}=\frac{\mathrm{1}+{e}^{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} } +\mathrm{2}\left(\frac{{x}}{{y}}\right)^{\mathrm{4}} }{\mathrm{2}\left(\frac{{x}}{{y}}\right){e}^{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} } } \\ $$$${let}\:{u}=\frac{{x}}{{y}},\:{i}.{e}.\:{x}={uy} \\ $$$$\frac{{dx}}{{dy}}={u}+{y}\frac{{du}}{{dy}} \\ $$$${u}+{y}\frac{{du}}{{dy}}=\frac{\mathrm{1}+{e}^{{u}^{\mathrm{2}} } +\mathrm{2}{u}^{\mathrm{4}} }{\mathrm{2}{ue}^{{u}^{\mathrm{2}} } } \\ $$$${y}\frac{{du}}{{dy}}=\frac{\mathrm{1}+{e}^{{u}^{\mathrm{2}} } +\mathrm{2}{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} {e}^{{u}^{\mathrm{2}} } }{\mathrm{2}{ue}^{{u}^{\mathrm{2}} } } \\ $$$$\frac{\mathrm{2}{ue}^{{u}^{\mathrm{2}} } }{\mathrm{1}+{e}^{{u}^{\mathrm{2}} } +\mathrm{2}{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} {e}^{{u}^{\mathrm{2}} } }{du}=\frac{{dy}}{{y}} \\ $$$$\frac{{e}^{{u}^{\mathrm{2}} } }{\mathrm{1}+{e}^{{u}^{\mathrm{2}} } +\mathrm{2}{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} {e}^{{u}^{\mathrm{2}} } }{du}^{\mathrm{2}} =\frac{{dy}}{{y}} \\ $$$${let}\:{t}={u}^{\mathrm{2}} \\ $$$$\frac{{e}^{{t}} }{\mathrm{1}+{e}^{{t}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{te}^{{t}} }{dt}=\frac{{dy}}{{y}} \\ $$$$\int\frac{{e}^{{t}} }{\mathrm{1}+{e}^{{t}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{te}^{{t}} }{dt}=\int\frac{{dy}}{{y}} \\ $$$$\int\frac{{e}^{{t}} }{\mathrm{1}+{e}^{{t}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{te}^{{t}} }{dt}=\mathrm{ln}\:\left({cy}\right) \\ $$$$…..\:\:{not}\:{integrable}\:… \\ $$
