Menu Close

Question-80015

Tinku Tara 0 Comments
Pin




Question Number 80015 by mr W last updated on 30/Jan/20
Commented by mr W last updated on 30/Jan/20
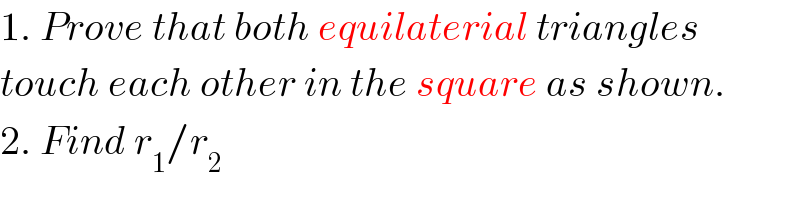
1. Prove that both equilaterial triangles touch each other in the square as shown. 2. Find r_1 /r_2
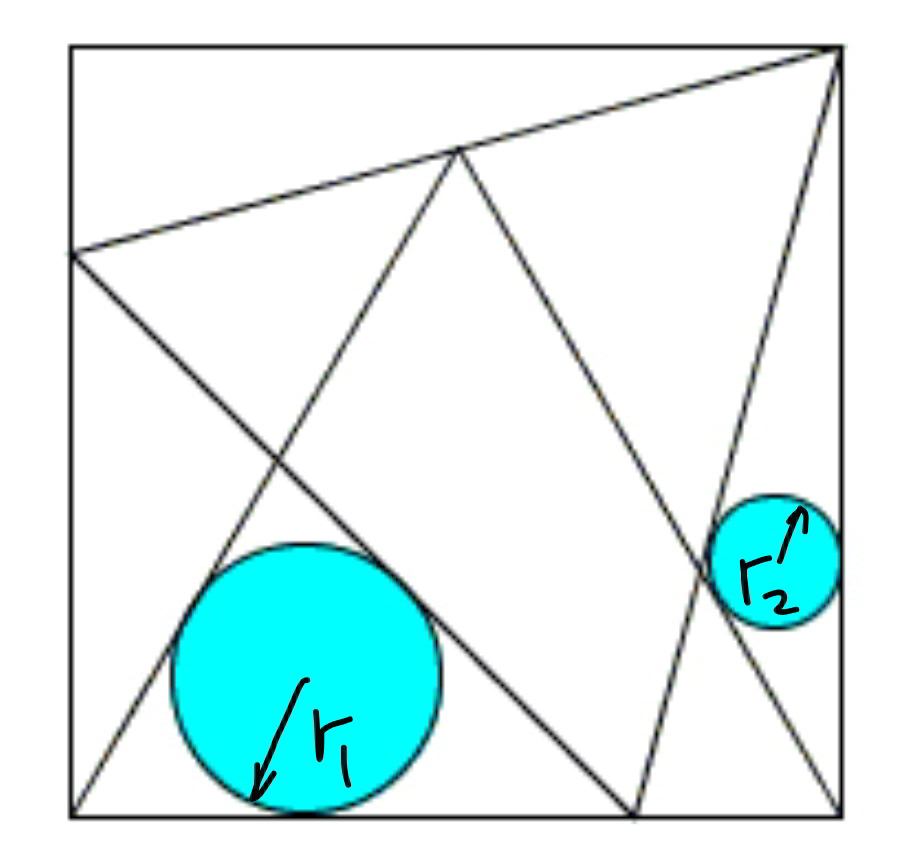
$$\mathrm{1}.\:{Prove}\:{that}\:{both}\:{equilaterial}\:{triangles} \\ $$$${touch}\:{each}\:{other}\:{in}\:{the}\:{square}\:{as}\:{shown}. \\ $$$$\mathrm{2}.\:{Find}\:{r}_{\mathrm{1}} /{r}_{\mathrm{2}} \\ $$
Commented by jagoll last updated on 30/Jan/20
circle againt
$${circle}\:{againt} \\ $$
Answered by mind is power last updated on 30/Jan/20
let ABCD square A(0,0);B(1,0) C(1,1) D(0,1) triangle ABE de Bas E is image of B by rootation center A angle 60 ⇒Z_E −Z_A =e^(i(π/3)) (Z_B −Z_A ) ⇒Z_E =((1/2)+((i(√3))/2))1 E((1/2),((√3)/2)) we get head of triangle the last one has C(1,1) and F=(CE)∩(AD) (CE):y=((((√3)/2)−1)/(−(1/2)))x+b y=(2−(√3))x+(√3)−1 F= { ((y=(2−(√3))x+(√3)−1)),((x=0)) :} ⇒y=(√3)−1⇒F(0,(√3)−1) the last Head G is obtined as Rootation of F by (π/3) center C Z_G =Z_c +((1/2)+((i(√3))/2))(Z_F −Z_c ) =(1+i)+(1/2)(1+i(√3))(i((√3)−1)−1−i) =(1+i)+(1/2)(1+i(√3))(i((√3)−2)−1) =1+i+(1/2)(−4+2(√3)−2i) =(−2+(√3)−i)+1+i =(√3)−1 G((√3)−1,0) ∈(AB) as show in diagramme This proof existence of such Triangle r_1 ,r_2 juste circle inside Two triangle witche we can find coordinate of head too be continued
$${let}\: \\ $$$${ABCD}\:{square} \\ $$$${A}\left(\mathrm{0},\mathrm{0}\right);{B}\left(\mathrm{1},\mathrm{0}\right)\:{C}\left(\mathrm{1},\mathrm{1}\right)\:{D}\left(\mathrm{0},\mathrm{1}\right) \\ $$$${triangle}\: \\ $$$${ABE}\:\:{de}\:{Bas} \\ $$$${E}\:{is}\:{image}\:{of}\:{B}\:{by}\:{rootation}\:{center}\:{A}\:{angle}\:\mathrm{60} \\ $$$$\Rightarrow{Z}_{{E}} −{Z}_{{A}} ={e}^{{i}\frac{\pi}{\mathrm{3}}} \left({Z}_{{B}} −{Z}_{{A}} \right) \\ $$$$\Rightarrow{Z}_{{E}} =\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\mathrm{1} \\ $$$${E}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${we}\:{get}\:{head}\:{of}\:{triangle} \\ $$$${the}\:{last}\:{one}\:{has}\:{C}\left(\mathrm{1},\mathrm{1}\right)\:\:{and}\:\:{F}=\left({CE}\right)\cap\left({AD}\right) \\ $$$$\left({CE}\right):{y}=\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{1}}{−\frac{\mathrm{1}}{\mathrm{2}}}{x}+{b} \\ $$$${y}=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){x}+\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$${F}=\begin{cases}{{y}=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){x}+\sqrt{\mathrm{3}}−\mathrm{1}}\\{{x}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow{y}=\sqrt{\mathrm{3}}−\mathrm{1}\Rightarrow{F}\left(\mathrm{0},\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$${the}\:{last}\:{Head}\:{G}\:{is}\:{obtined}\:{as}\:{Rootation}\:{of}\:{F}\:{by}\:\frac{\pi}{\mathrm{3}}\:{center}\:{C} \\ $$$${Z}_{{G}} ={Z}_{{c}} +\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left({Z}_{{F}} −{Z}_{{c}} \right) \\ $$$$=\left(\mathrm{1}+{i}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)\left({i}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)−\mathrm{1}−{i}\right) \\ $$$$=\left(\mathrm{1}+{i}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)\left({i}\left(\sqrt{\mathrm{3}}−\mathrm{2}\right)−\mathrm{1}\right) \\ $$$$=\mathrm{1}+{i}+\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}{i}\right) \\ $$$$=\left(−\mathrm{2}+\sqrt{\mathrm{3}}−{i}\right)+\mathrm{1}+{i} \\ $$$$=\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$${G}\left(\sqrt{\mathrm{3}}−\mathrm{1},\mathrm{0}\right)\:\:\in\left({AB}\right)\:{as}\:{show}\:{in}\:{diagramme} \\ $$$${This}\:{proof}\:{existence}\:{of}\:{such}\:{Triangle} \\ $$$${r}_{\mathrm{1}} ,{r}_{\mathrm{2}} \:{juste}\:{circle}\:{inside}\:{Two}\:{triangle}\:\:{witche}\:{we}\:{can}\:{find} \\ $$$${coordinate}\:{of}\:{head}\:{too}\:{be}\:{continued} \\ $$$$ \\ $$
Answered by ajfour last updated on 30/Jan/20
Commented by ajfour last updated on 30/Jan/20
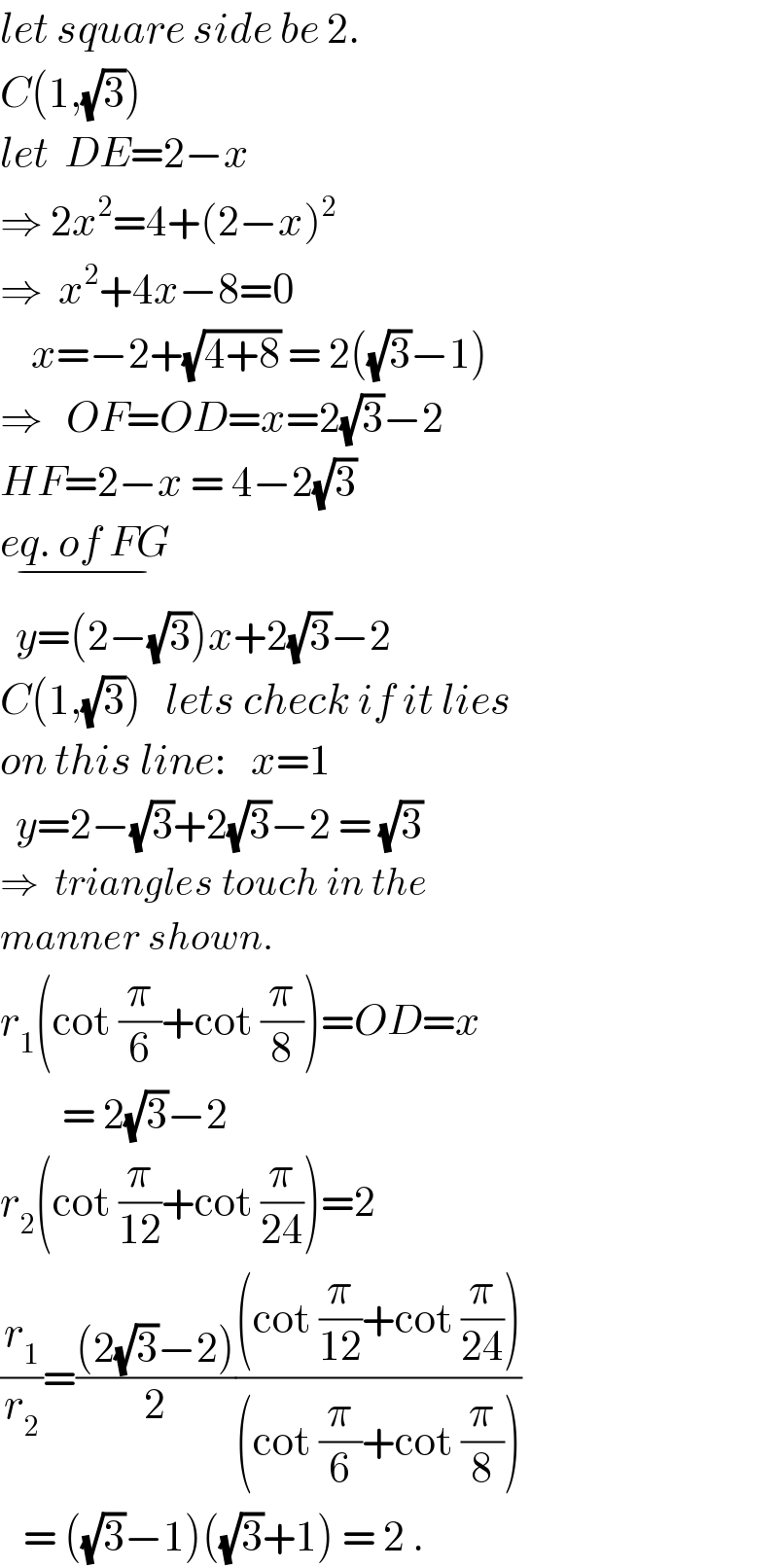
let square side be 2. C(1,(√3)) let DE=2−x ⇒ 2x^2 =4+(2−x)^2 ⇒ x^2 +4x−8=0 x=−2+(√(4+8)) = 2((√3)−1) ⇒ OF=OD=x=2(√3)−2 HF=2−x = 4−2(√3) eq. of FG_(−) y=(2−(√3))x+2(√3)−2 C(1,(√3)) lets check if it lies on this line: x=1 y=2−(√3)+2(√3)−2 = (√3) ⇒ triangles touch in the manner shown. r_1 (cot (π/6)+cot (π/8))=OD=x = 2(√3)−2 r_2 (cot (π/(12))+cot (π/(24)))=2 (r_1 /r_2 )=(((2(√3)−2))/2)(((cot (π/(12))+cot (π/(24))))/((cot (π/6)+cot (π/8)))) = ((√3)−1)((√3)+1) = 2 .
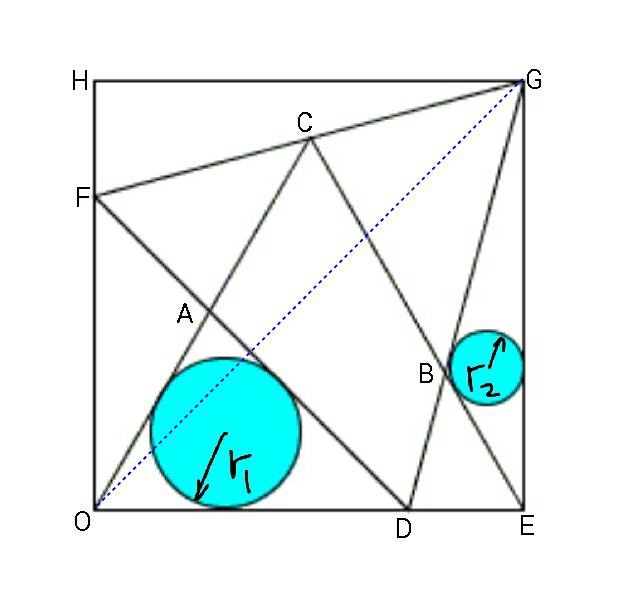
$${let}\:{square}\:{side}\:{be}\:\mathrm{2}. \\ $$$${C}\left(\mathrm{1},\sqrt{\mathrm{3}}\right) \\ $$$${let}\:\:{DE}=\mathrm{2}−{x} \\ $$$$\Rightarrow\:\mathrm{2}{x}^{\mathrm{2}} =\mathrm{4}+\left(\mathrm{2}−{x}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{8}=\mathrm{0} \\ $$$$\:\:\:\:{x}=−\mathrm{2}+\sqrt{\mathrm{4}+\mathrm{8}}\:=\:\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\:{OF}={OD}={x}=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2} \\ $$$${HF}=\mathrm{2}−{x}\:=\:\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\underset{−} {{eq}.\:{of}\:{FG}} \\ $$$$\:\:{y}=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){x}+\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2} \\ $$$${C}\left(\mathrm{1},\sqrt{\mathrm{3}}\right)\:\:\:{lets}\:{check}\:{if}\:{it}\:{lies} \\ $$$${on}\:{this}\:{line}:\:\:\:{x}=\mathrm{1} \\ $$$$\:\:{y}=\mathrm{2}−\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}\:=\:\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:\:{triangles}\:{touch}\:{in}\:{the} \\ $$$${manner}\:{shown}. \\ $$$${r}_{\mathrm{1}} \left(\mathrm{cot}\:\frac{\pi}{\mathrm{6}}+\mathrm{cot}\:\frac{\pi}{\mathrm{8}}\right)={OD}={x} \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2} \\ $$$${r}_{\mathrm{2}} \left(\mathrm{cot}\:\frac{\pi}{\mathrm{12}}+\mathrm{cot}\:\frac{\pi}{\mathrm{24}}\right)=\mathrm{2} \\ $$$$\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }=\frac{\left(\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}\right)}{\mathrm{2}}\frac{\left(\mathrm{cot}\:\frac{\pi}{\mathrm{12}}+\mathrm{cot}\:\frac{\pi}{\mathrm{24}}\right)}{\left(\mathrm{cot}\:\frac{\pi}{\mathrm{6}}+\mathrm{cot}\:\frac{\pi}{\mathrm{8}}\right)} \\ $$$$\:\:\:=\:\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)\:=\:\mathrm{2}\:. \\ $$
Commented by mr W last updated on 30/Jan/20
thank you sir! perfectly solved!
$${thank}\:{you}\:{sir}!\:{perfectly}\:{solved}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *