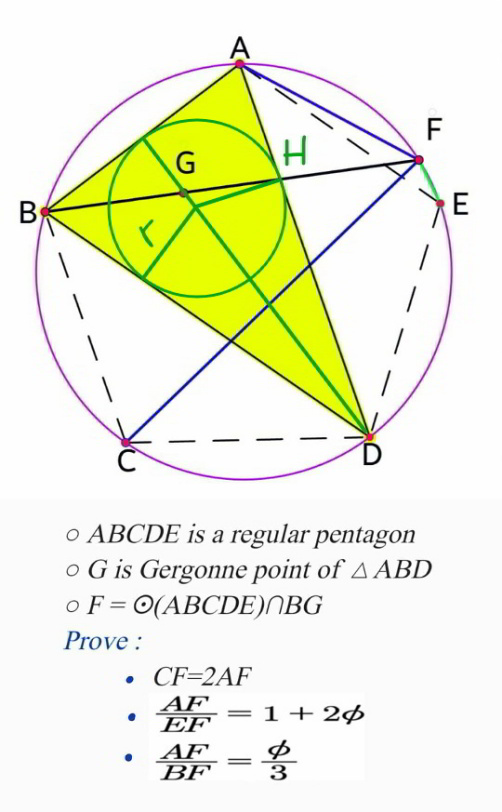
Question Number 80119 by M±th+et£s last updated on 31/Jan/20
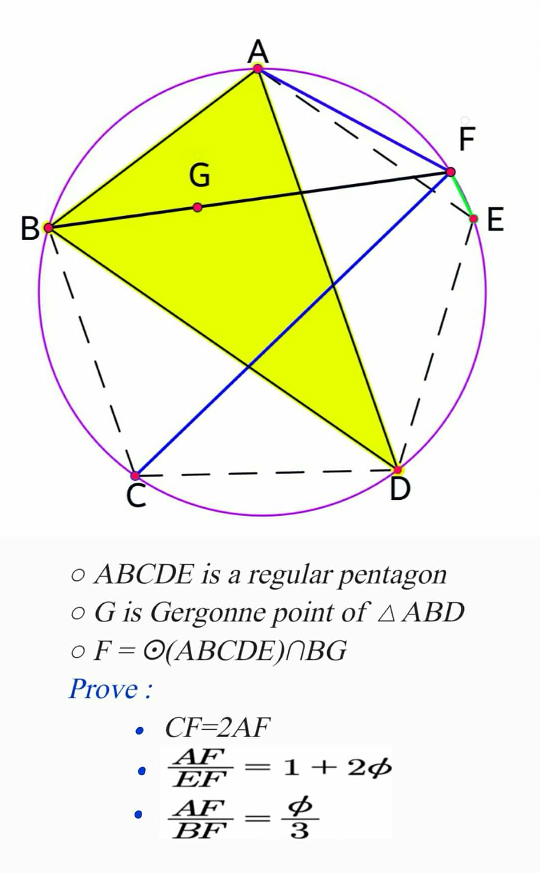
Answered by key of knowledge last updated on 31/Jan/20
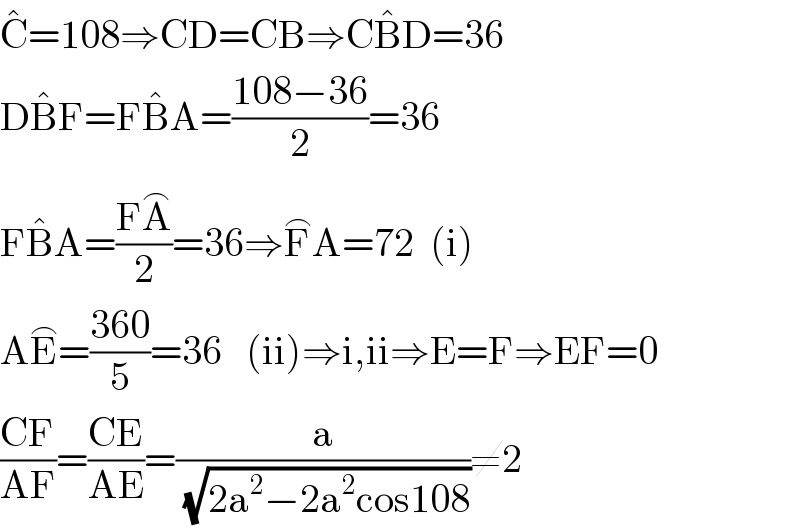
$$\hat {\mathrm{C}}=\mathrm{108}\Rightarrow\mathrm{CD}=\mathrm{CB}\Rightarrow\mathrm{C}\hat {\mathrm{B}D}=\mathrm{36} \\ $$$$\mathrm{D}\hat {\mathrm{B}F}=\mathrm{F}\hat {\mathrm{B}A}=\frac{\mathrm{108}−\mathrm{36}}{\mathrm{2}}=\mathrm{36} \\ $$$$\mathrm{F}\hat {\mathrm{B}A}=\frac{\mathrm{F}\overset{\frown} {\mathrm{A}}}{\mathrm{2}}=\mathrm{36}\Rightarrow\overset{\frown} {\mathrm{F}A}=\mathrm{72}\:\:\left(\mathrm{i}\right) \\ $$$$\mathrm{A}\overset{\frown} {\mathrm{E}}=\frac{\mathrm{360}}{\mathrm{5}}=\mathrm{36}\:\:\:\left(\mathrm{ii}\right)\Rightarrow\mathrm{i},\mathrm{ii}\Rightarrow\mathrm{E}=\mathrm{F}\Rightarrow\mathrm{EF}=\mathrm{0} \\ $$$$\frac{\mathrm{CF}}{\mathrm{AF}}=\frac{\mathrm{CE}}{\mathrm{AE}}=\frac{\mathrm{a}}{\:\sqrt{\mathrm{2a}^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} \mathrm{cos108}}}\neq\mathrm{2} \\ $$
Answered by mr W last updated on 31/Jan/20