Question Number 80131 by M±th+et£s last updated on 31/Jan/20
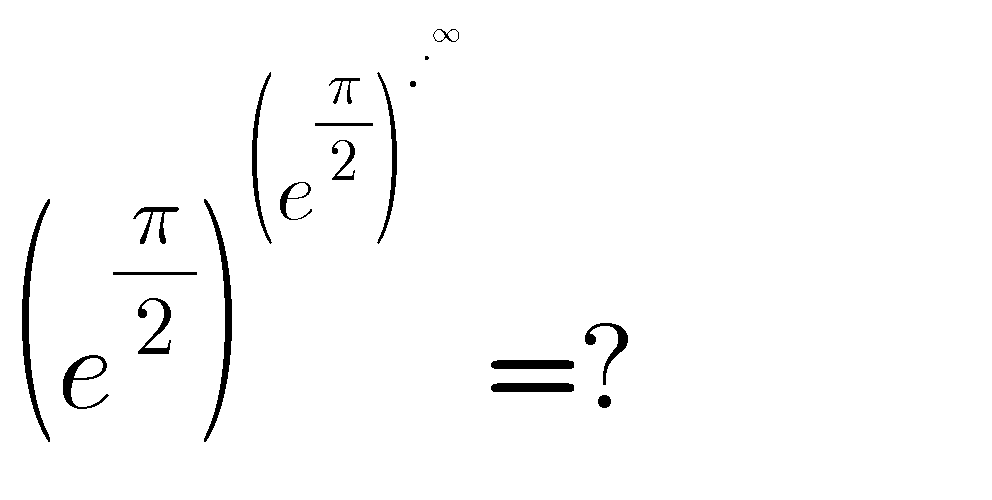
Commented by MJS last updated on 31/Jan/20

$$+\infty \\ $$$$\mathrm{e}^{\frac{\pi}{\mathrm{2}}} \approx\mathrm{4}.\mathrm{8} \\ $$$$\mathrm{4}.\mathrm{8}^{\mathrm{4}.\mathrm{8}} \approx\mathrm{1913} \\ $$$$… \\ $$
Commented by mr W last updated on 31/Jan/20
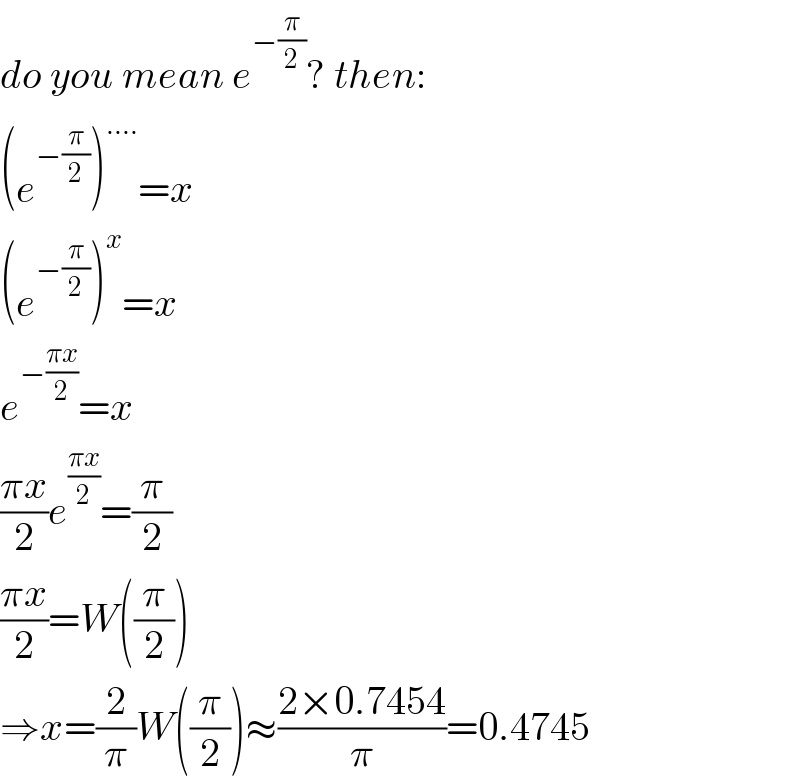
$${do}\:{you}\:{mean}\:{e}^{−\frac{\pi}{\mathrm{2}}} ?\:{then}: \\ $$$$\left({e}^{−\frac{\pi}{\mathrm{2}}} \right)^{….} ={x} \\ $$$$\left({e}^{−\frac{\pi}{\mathrm{2}}} \right)^{{x}} ={x} \\ $$$${e}^{−\frac{\pi{x}}{\mathrm{2}}} ={x} \\ $$$$\frac{\pi{x}}{\mathrm{2}}{e}^{\frac{\pi{x}}{\mathrm{2}}} =\frac{\pi}{\mathrm{2}} \\ $$$$\frac{\pi{x}}{\mathrm{2}}={W}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}}{\pi}{W}\left(\frac{\pi}{\mathrm{2}}\right)\approx\frac{\mathrm{2}×\mathrm{0}.\mathrm{7454}}{\pi}=\mathrm{0}.\mathrm{4745} \\ $$
