Question Number 80204 by jagoll last updated on 01/Feb/20

Commented by Tony Lin last updated on 01/Feb/20
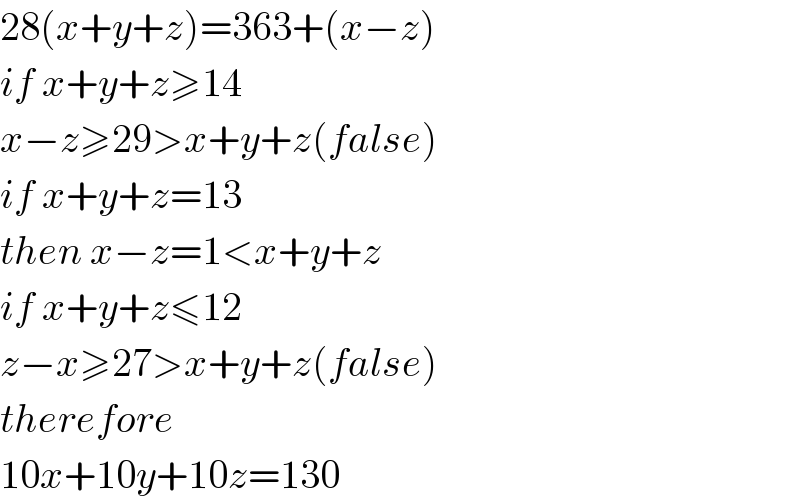
$$\mathrm{28}\left({x}+{y}+{z}\right)=\mathrm{363}+\left({x}−{z}\right) \\ $$$${if}\:{x}+{y}+{z}\geqslant\mathrm{14} \\ $$$${x}−{z}\geqslant\mathrm{29}>{x}+{y}+{z}\left({false}\right) \\ $$$${if}\:{x}+{y}+{z}=\mathrm{13} \\ $$$${then}\:{x}−{z}=\mathrm{1}<{x}+{y}+{z} \\ $$$${if}\:{x}+{y}+{z}\leqslant\mathrm{12} \\ $$$${z}−{x}\geqslant\mathrm{27}>{x}+{y}+{z}\left({false}\right) \\ $$$${therefore} \\ $$$$\mathrm{10}{x}+\mathrm{10}{y}+\mathrm{10}{z}=\mathrm{130} \\ $$
Commented by jagoll last updated on 01/Feb/20

$${thank}\:{you}\:{sir} \\ $$
