Question-80207

Question Number 80207 by peter frank last updated on 01/Feb/20

Commented by john santu last updated on 01/Feb/20

(2) area = (1/2)∣ determinant (((2 1)),((3 −2)))+ determinant (((3 −2)),((x x+3)))+ determinant (((x x+3)),((2 1)))∣ ⇒ 5 =(1/2)∣(−7)+(5x+9)+(−x−6)∣ ⇒ 10 = ∣4x−4∣ ± 5 = 2x−2 , 2x=2±5 ⇒ { ((x=(7/3), y=((16)/3))),((x=−(3/2), y=(3/2))) :} therefore the third vertices triangle is ((7/3),((16)/3)) and (−(3/2),(3/2))

$$\left(\mathrm{2}\right)\:{area}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mid\begin{vmatrix}{\mathrm{2}\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{3}\:\:−\mathrm{2}}\end{vmatrix}+\begin{vmatrix}{\mathrm{3}\:\:\:\:\:\:−\mathrm{2}}\\{{x}\:\:\:\:{x}+\mathrm{3}}\end{vmatrix}+\begin{vmatrix}{{x}\:\:\:\:{x}+\mathrm{3}}\\{\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{1}}\end{vmatrix}\mid \\ $$$$\Rightarrow\:\mathrm{5}\:=\frac{\mathrm{1}}{\mathrm{2}}\mid\left(−\mathrm{7}\right)+\left(\mathrm{5}{x}+\mathrm{9}\right)+\left(−{x}−\mathrm{6}\right)\mid \\ $$$$\Rightarrow\:\mathrm{10}\:=\:\mid\mathrm{4}{x}−\mathrm{4}\mid\: \\ $$$$\pm\:\mathrm{5}\:=\:\mathrm{2}{x}−\mathrm{2}\:,\:\mathrm{2}{x}=\mathrm{2}\pm\mathrm{5}\:\Rightarrow\begin{cases}{{x}=\frac{\mathrm{7}}{\mathrm{3}},\:{y}=\frac{\mathrm{16}}{\mathrm{3}}}\\{{x}=−\frac{\mathrm{3}}{\mathrm{2}},\:{y}=\frac{\mathrm{3}}{\mathrm{2}}}\end{cases} \\ $$$${therefore}\:{the}\:{third}\:{vertices}\:{triangle} \\ $$$${is}\:\left(\frac{\mathrm{7}}{\mathrm{3}},\frac{\mathrm{16}}{\mathrm{3}}\right)\:{and}\:\left(−\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$

Commented by mr W last updated on 01/Feb/20

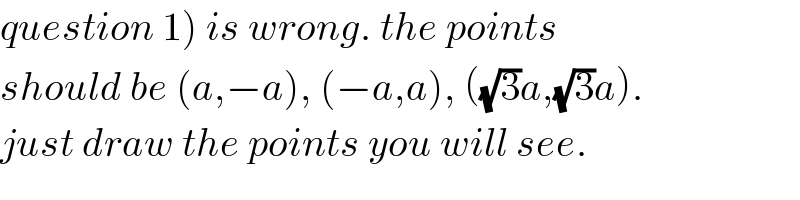
question 1) is wrong. the points should be (a,−a), (−a,a), ((√3)a,(√3)a). just draw the points you will see.

$$\left.{question}\:\mathrm{1}\right)\:{is}\:{wrong}.\:{the}\:{points}\: \\ $$$${should}\:{be}\:\left({a},−{a}\right),\:\left(−{a},{a}\right),\:\left(\sqrt{\mathrm{3}}{a},\sqrt{\mathrm{3}}{a}\right). \\ $$$${just}\:{draw}\:{the}\:{points}\:{you}\:{will}\:{see}. \\ $$

Commented by peter frank last updated on 01/Feb/20

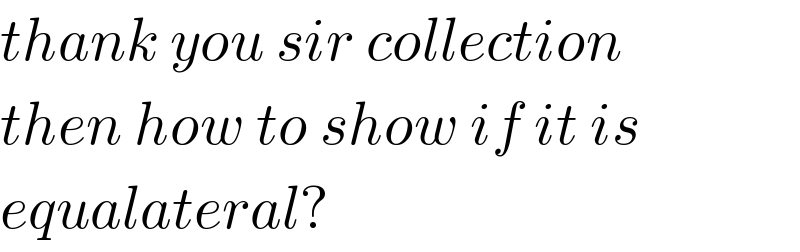
$${thank}\:{you}\:{sir}\:{collection} \\ $$$${then}\:{how}\:{to}\:{show}\:{if}\:{it}\:{is} \\ $$$${equalateral}? \\ $$

Commented by mr W last updated on 01/Feb/20

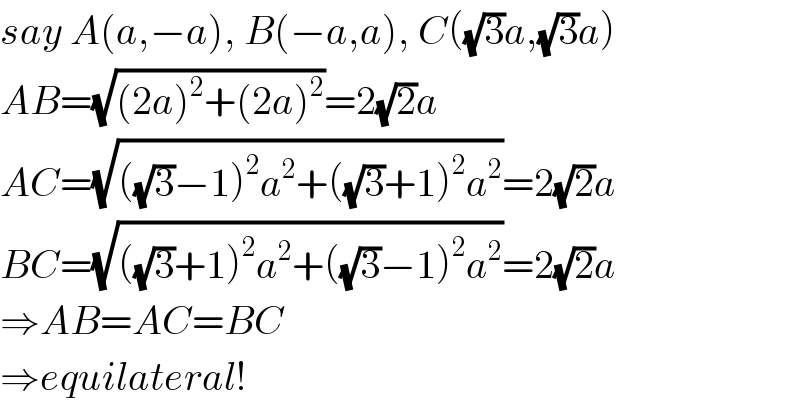
say A(a,−a), B(−a,a), C((√3)a,(√3)a) AB=(√((2a)^2 +(2a)^2 ))=2(√2)a AC=(√(((√3)−1)^2 a^2 +((√3)+1)^2 a^2 ))=2(√2)a BC=(√(((√3)+1)^2 a^2 +((√3)−1)^2 a^2 ))=2(√2)a ⇒AB=AC=BC ⇒equilateral!

$${say}\:{A}\left({a},−{a}\right),\:{B}\left(−{a},{a}\right),\:{C}\left(\sqrt{\mathrm{3}}{a},\sqrt{\mathrm{3}}{a}\right) \\ $$$${AB}=\sqrt{\left(\mathrm{2}{a}\right)^{\mathrm{2}} +\left(\mathrm{2}{a}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{2}}{a} \\ $$$${AC}=\sqrt{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{2}}{a} \\ $$$${BC}=\sqrt{\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{2}}{a} \\ $$$$\Rightarrow{AB}={AC}={BC} \\ $$$$\Rightarrow{equilateral}! \\ $$

Commented by kaivan.ahmadi last updated on 01/Feb/20

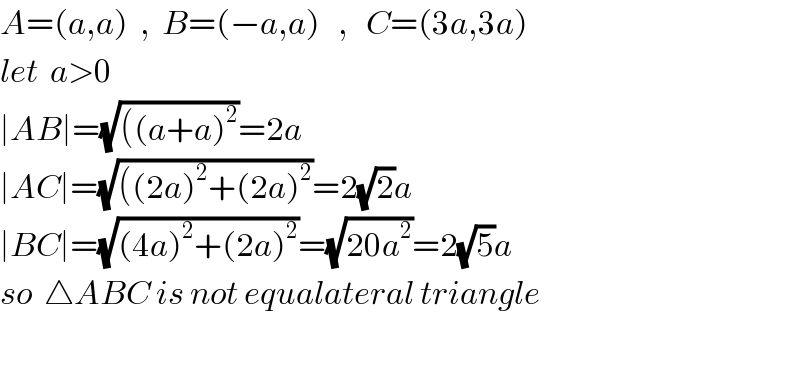
A=(a,a) , B=(−a,a) , C=(3a,3a) let a>0 ∣AB∣=(√(((a+a)^2 ))=2a ∣AC∣=(√(((2a)^2 +(2a)^2 ))=2(√2)a ∣BC∣=(√((4a)^2 +(2a)^2 ))=(√(20a^2 ))=2(√5)a so △ABC is not equalateral triangle

$${A}=\left({a},{a}\right)\:\:,\:\:{B}=\left(−{a},{a}\right)\:\:\:,\:\:\:{C}=\left(\mathrm{3}{a},\mathrm{3}{a}\right) \\ $$$${let}\:\:{a}>\mathrm{0} \\ $$$$\mid{AB}\mid=\sqrt{\left(\left({a}+{a}\right)^{\mathrm{2}} \right.}=\mathrm{2}{a} \\ $$$$\mid{AC}\mid=\sqrt{\left(\left(\mathrm{2}{a}\right)^{\mathrm{2}} +\left(\mathrm{2}{a}\right)^{\mathrm{2}} \right.}=\mathrm{2}\sqrt{\mathrm{2}}{a} \\ $$$$\mid{BC}\mid=\sqrt{\left(\mathrm{4}{a}\right)^{\mathrm{2}} +\left(\mathrm{2}{a}\right)^{\mathrm{2}} }=\sqrt{\mathrm{20}{a}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{5}}{a} \\ $$$${so}\:\:\bigtriangleup{ABC}\:{is}\:{not}\:{equalateral}\:{triangle} \\ $$$$ \\ $$

Commented by peter frank last updated on 01/Feb/20

$${I}\:{appriciate}\:{your}\:{time}\:{sir}.{thank}\:{you} \\ $$$${mr}\:{w}\:\&{kaivan} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply