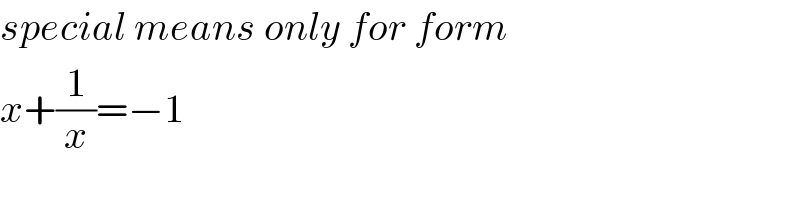Question Number 80209 by peter frank last updated on 01/Feb/20

Commented by mathmax by abdo last updated on 01/Feb/20
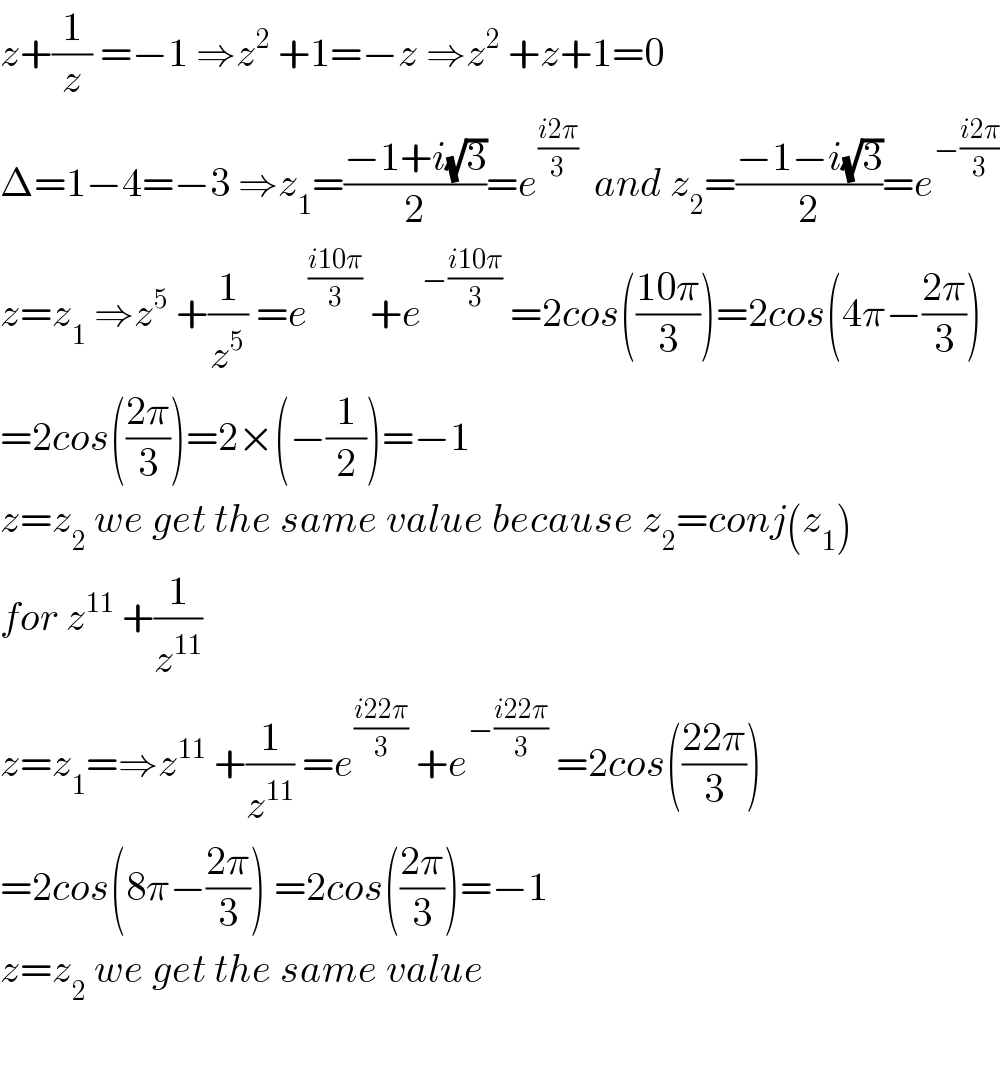
Answered by som(math1967) last updated on 01/Feb/20
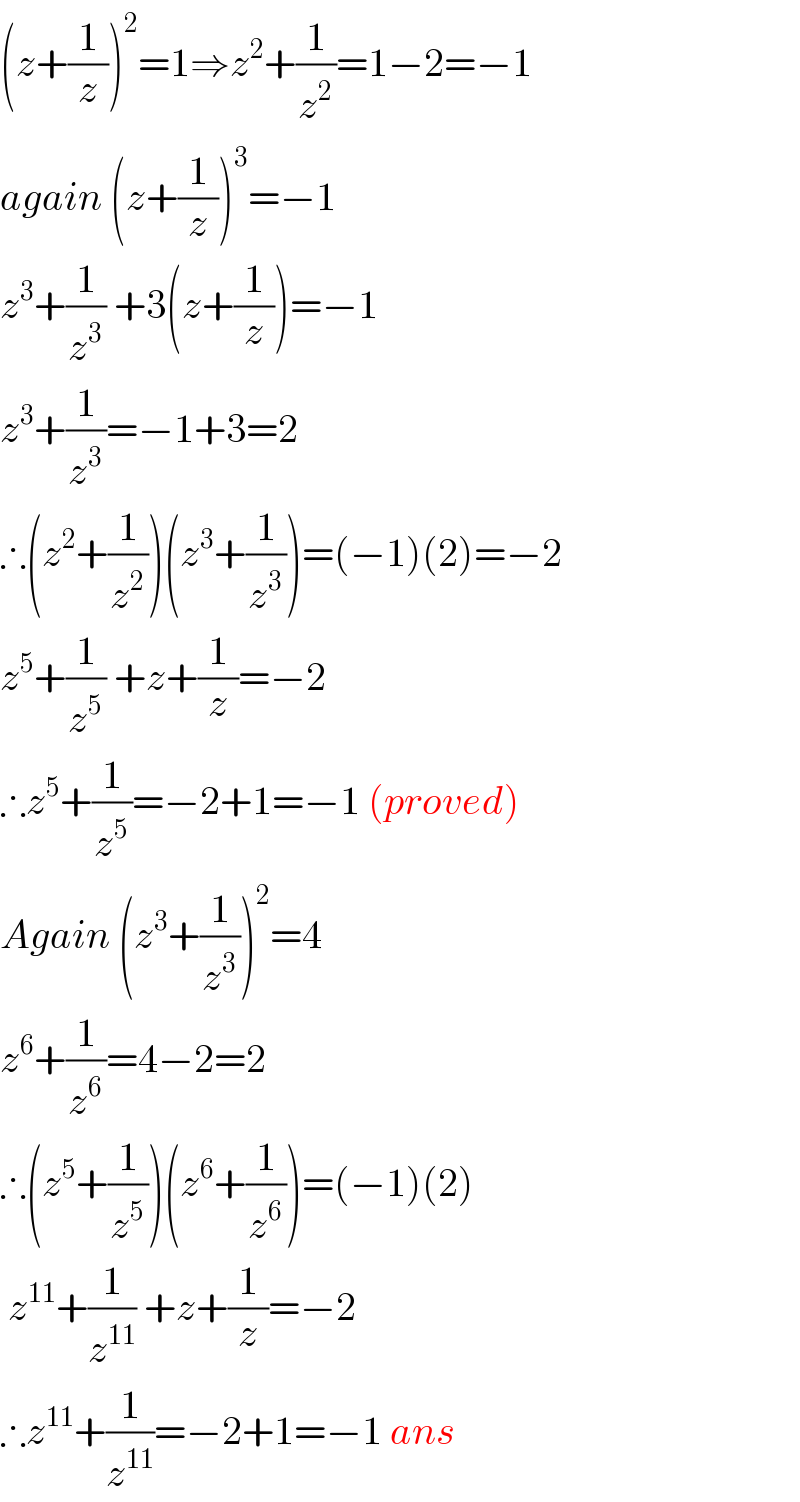
Answered by mr W last updated on 01/Feb/20
![z+(1/z)=−1 z^2 +z+1=0 z=((−1±i(√3))/2)=−{cos (±(π/3))+sin (±(π/3)) i}=−e^(±(π/3)i) z^n +(1/z^n )=(−1)^n [e^(±((nπ)/3)i) +e^(∓((nπ)/3)i) ] =2(−1)^n cos (±((nπ)/3)) =2(−1)^n cos (((nπ)/3)) ⇒z^n +(1/z^n )=2(−1)^n cos (((nπ)/3)) n=5: z^5 +(1/z^5 )=2(−1)^5 cos (((5π)/3))=−2×(1/2)=−1 n=11: z^(11) +(1/z^(11) )=2(−1)^(11) cos (((11π)/3))=−2×(1/2)=−1 n=3: z^3 +(1/z^3 )=2(−1)^3 cos (((3π)/3))=−2×(−1)=2 n=12: z^(12) +(1/z^(12) )=2(−1)^(12) cos (((12π)/3))=2×1=2](https://www.tinkutara.com/question/Q80216.png)
Commented by jagoll last updated on 01/Feb/20
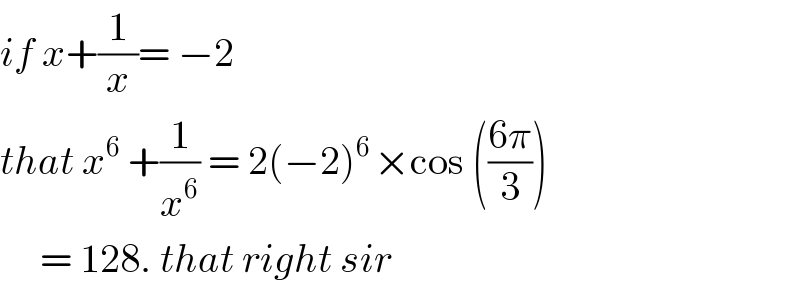
Commented by mr W last updated on 01/Feb/20
Commented by peter frank last updated on 01/Feb/20
Commented by mr W last updated on 01/Feb/20
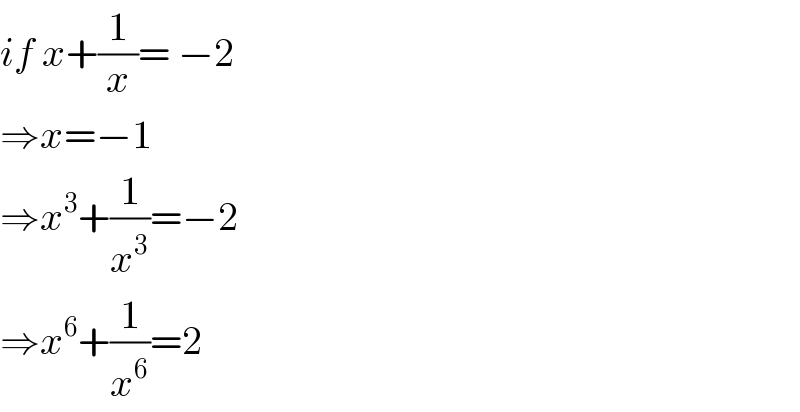
Commented by jagoll last updated on 01/Feb/20