Question Number 80220 by TawaTawa last updated on 01/Feb/20

Commented by kaivan.ahmadi last updated on 01/Feb/20
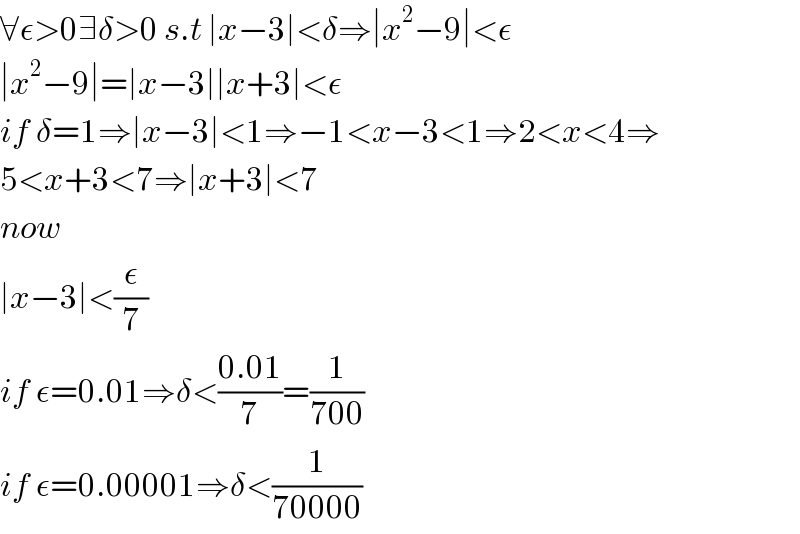
$$\forall\epsilon>\mathrm{0}\exists\delta>\mathrm{0}\:{s}.{t}\:\mid{x}−\mathrm{3}\mid<\delta\Rightarrow\mid{x}^{\mathrm{2}} −\mathrm{9}\mid<\epsilon \\ $$$$\mid{x}^{\mathrm{2}} −\mathrm{9}\mid=\mid{x}−\mathrm{3}\mid\mid{x}+\mathrm{3}\mid<\epsilon \\ $$$${if}\:\delta=\mathrm{1}\Rightarrow\mid{x}−\mathrm{3}\mid<\mathrm{1}\Rightarrow−\mathrm{1}<{x}−\mathrm{3}<\mathrm{1}\Rightarrow\mathrm{2}<{x}<\mathrm{4}\Rightarrow \\ $$$$\mathrm{5}<{x}+\mathrm{3}<\mathrm{7}\Rightarrow\mid{x}+\mathrm{3}\mid<\mathrm{7} \\ $$$${now} \\ $$$$\mid{x}−\mathrm{3}\mid<\frac{\epsilon}{\mathrm{7}} \\ $$$${if}\:\epsilon=\mathrm{0}.\mathrm{01}\Rightarrow\delta<\frac{\mathrm{0}.\mathrm{01}}{\mathrm{7}}=\frac{\mathrm{1}}{\mathrm{700}} \\ $$$${if}\:\epsilon=\mathrm{0}.\mathrm{00001}\Rightarrow\delta<\frac{\mathrm{1}}{\mathrm{70000}} \\ $$
Commented by TawaTawa last updated on 01/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 01/Feb/20
$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{come}\:\mathrm{across}\:\:\mathrm{5}\:\mathrm{and}\:\mathrm{7}\:\:\mathrm{sir} \\ $$
