Question Number 80222 by mr W last updated on 01/Feb/20

Commented by mr W last updated on 01/Feb/20

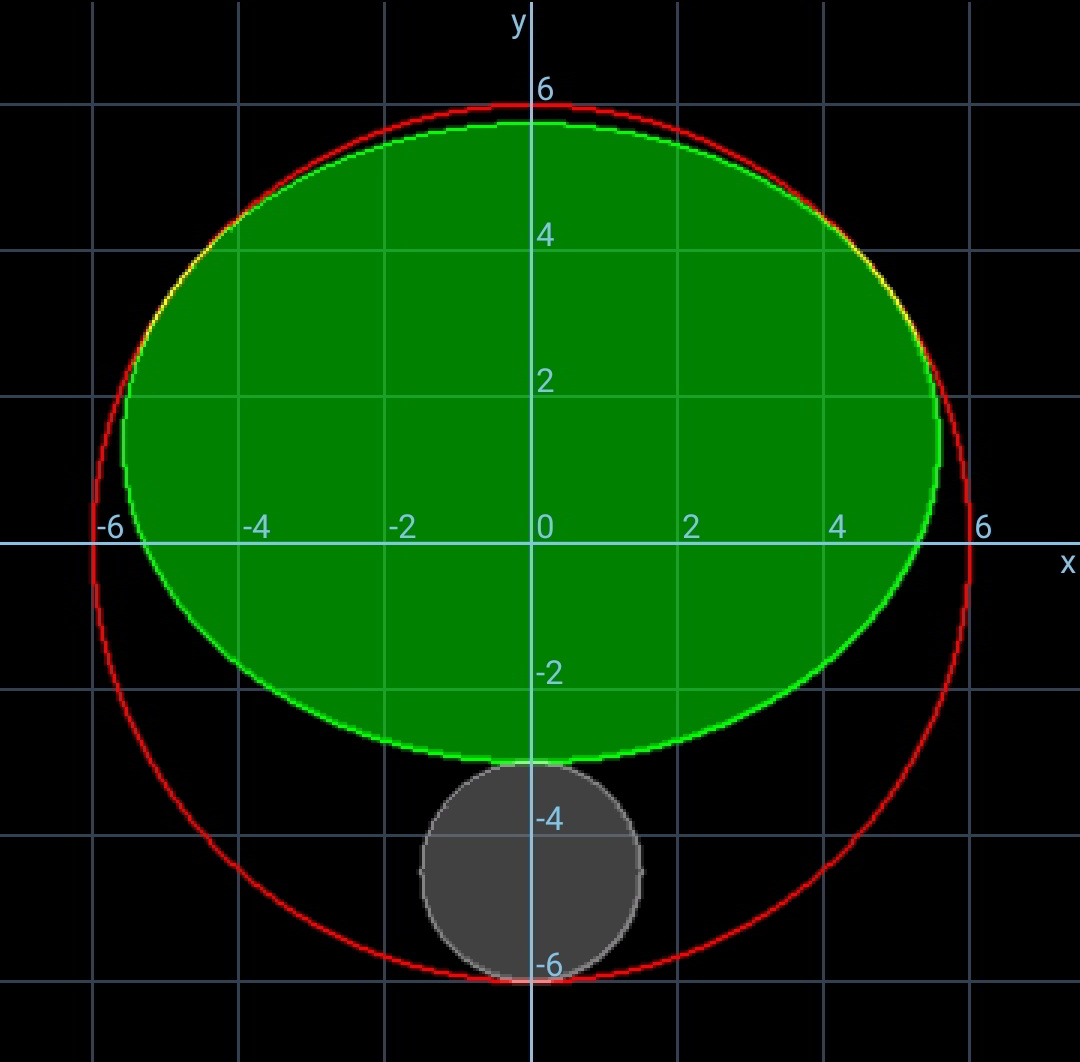
$${A}\:{round}\:{steel}\:{plate}\:{with}\:{radius}\:{R}\:{has} \\ $$$${a}\:{round}\:{hole}\:{with}\:{radius}\:{r}\:{as}\:{shown}. \\ $$$${Was}\:{is}\:{the}\:{maximal}\:{area}\:{of}\:{the}\:{ellipse} \\ $$$${which}\:{can}\:{be}\:{cut}\:{off}\:{from}\:{the}\:{plate}? \\ $$
Commented by behi83417@gmail.com last updated on 01/Feb/20

$$\mathrm{dear}\:\mathrm{master}!\mathrm{please}\:\mathrm{see}\:\mathrm{my}\:\mathrm{commenet}\:\mathrm{on} \\ $$$$\mathrm{Q}#\mathrm{80142}.\mathrm{thank}\:\mathrm{you}. \\ $$
Answered by mr W last updated on 02/Feb/20

Commented by mr W last updated on 02/Feb/20
![parameters of ellipse: a, b center of ellipse: C(0,c) b−c=R−2r ⇒c=b+2r−R eqn. of big circle: x^2 +y^2 =R^2 eqn. of ellipse: (x^2 /a^2 )+(((y−c)^2 )/b^2 )=1 intersection from circle and ellipse: ((R^2 −y^2 )/a^2 )+(((y−c)^2 )/b^2 )=1 b^2 (R^2 −y^2 )+a^2 (y−c)^2 =a^2 b^2 (a^2 −b^2 )y^2 −2ca^2 y+a^2 c^2 −a^2 b^2 +R^2 b^2 =0 due to tangency Δ=0: c^2 a^4 −(a^2 −b^2 )(a^2 c^2 −a^2 b^2 +R^2 b^2 )=0 a^2 (a^2 −b^2 −R^2 +c^2 )+R^2 b^2 =0 a^4 −4r(R−r)a^2 −2(R−2r)a^2 b+R^2 b^2 =0 ⇒b=(((R−2r)a^2 +2a(√(r(R−r)(R^2 −a^2 ))))/R^2 ) let P=ab a^6 −4r(R−r)a^4 −2(R−2r)a^3 P+R^2 P^2 =0 6a^5 −16r(R−r)a^3 −2(R−2r)(3a^2 P+a^3 (dP/da))+2R^2 P(dP/da)=0 for maximum ellipse, (dP/da)=0 3a^2 −8r(R−r)=3(R−2r)b 3a^2 −2R^2 =((3(R−2r))/(2r(R−r)))a(√(r(R−r)(R^2 −a^2 ))) [9+((9(R−2r)^2 )/(4r(R−r)))]a^4 −[12+((9(R−2r)^2 )/(4r(R−r)))]R^2 a^2 +4R^4 =0 with μ=((9(R−2r)^2 )/(4r(R−r))) ⇒(9+μ)((a/R))^4 −(12+μ)((a/R))^2 +4=0 ⇒(a/R)=(√((12+μ±(√(μ(8+μ))))/(2(9+μ)))) (“+” if R>2r, “−” if R<2r)](https://www.tinkutara.com/question/Q80313.png)
$${parameters}\:{of}\:{ellipse}:\:{a},\:{b} \\ $$$${center}\:{of}\:{ellipse}:\:{C}\left(\mathrm{0},{c}\right) \\ $$$${b}−{c}={R}−\mathrm{2}{r}\:\Rightarrow{c}={b}+\mathrm{2}{r}−{R} \\ $$$$ \\ $$$${eqn}.\:{of}\:{big}\:{circle}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${eqn}.\:{of}\:{ellipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{c}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$ \\ $$$${intersection}\:{from}\:{circle}\:{and}\:{ellipse}: \\ $$$$\frac{{R}^{\mathrm{2}} −{y}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{c}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${b}^{\mathrm{2}} \left({R}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} \left({y}−{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){y}^{\mathrm{2}} −\mathrm{2}{ca}^{\mathrm{2}} {y}+{a}^{\mathrm{2}} {c}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{R}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$${due}\:{to}\:{tangency}\:\Delta=\mathrm{0}: \\ $$$${c}^{\mathrm{2}} {a}^{\mathrm{4}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} {c}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{R}^{\mathrm{2}} {b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{R}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+{R}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{4}} −\mathrm{4}{r}\left({R}−{r}\right){a}^{\mathrm{2}} −\mathrm{2}\left({R}−\mathrm{2}{r}\right){a}^{\mathrm{2}} {b}+{R}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{b}=\frac{\left({R}−\mathrm{2}{r}\right){a}^{\mathrm{2}} +\mathrm{2}{a}\sqrt{{r}\left({R}−{r}\right)\left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}}{{R}^{\mathrm{2}} } \\ $$$${let}\:{P}={ab} \\ $$$${a}^{\mathrm{6}} −\mathrm{4}{r}\left({R}−{r}\right){a}^{\mathrm{4}} −\mathrm{2}\left({R}−\mathrm{2}{r}\right){a}^{\mathrm{3}} {P}+{R}^{\mathrm{2}} {P}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{6}{a}^{\mathrm{5}} −\mathrm{16}{r}\left({R}−{r}\right){a}^{\mathrm{3}} −\mathrm{2}\left({R}−\mathrm{2}{r}\right)\left(\mathrm{3}{a}^{\mathrm{2}} {P}+{a}^{\mathrm{3}} \frac{{dP}}{{da}}\right)+\mathrm{2}{R}^{\mathrm{2}} {P}\frac{{dP}}{{da}}=\mathrm{0} \\ $$$${for}\:{maximum}\:{ellipse},\:\frac{{dP}}{{da}}=\mathrm{0} \\ $$$$\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{r}\left({R}−{r}\right)=\mathrm{3}\left({R}−\mathrm{2}{r}\right){b} \\ $$$$\mathrm{3}{a}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} =\frac{\mathrm{3}\left({R}−\mathrm{2}{r}\right)}{\mathrm{2}{r}\left({R}−{r}\right)}{a}\sqrt{{r}\left({R}−{r}\right)\left({R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)} \\ $$$$\left[\mathrm{9}+\frac{\mathrm{9}\left({R}−\mathrm{2}{r}\right)^{\mathrm{2}} }{\mathrm{4}{r}\left({R}−{r}\right)}\right]{a}^{\mathrm{4}} −\left[\mathrm{12}+\frac{\mathrm{9}\left({R}−\mathrm{2}{r}\right)^{\mathrm{2}} }{\mathrm{4}{r}\left({R}−{r}\right)}\right]{R}^{\mathrm{2}} {a}^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{4}} =\mathrm{0} \\ $$$${with}\:\mu=\frac{\mathrm{9}\left({R}−\mathrm{2}{r}\right)^{\mathrm{2}} }{\mathrm{4}{r}\left({R}−{r}\right)} \\ $$$$\Rightarrow\left(\mathrm{9}+\mu\right)\left(\frac{{a}}{{R}}\right)^{\mathrm{4}} −\left(\mathrm{12}+\mu\right)\left(\frac{{a}}{{R}}\right)^{\mathrm{2}} +\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\frac{{a}}{{R}}=\sqrt{\frac{\mathrm{12}+\mu\pm\sqrt{\mu\left(\mathrm{8}+\mu\right)}}{\mathrm{2}\left(\mathrm{9}+\mu\right)}} \\ $$$$\left(“+''\:{if}\:{R}>\mathrm{2}{r},\:“−''\:{if}\:{R}<\mathrm{2}{r}\right) \\ $$
Commented by mr W last updated on 02/Feb/20
Commented by mr W last updated on 02/Feb/20

Commented by mr W last updated on 02/Feb/20

