Question Number 80386 by gny last updated on 02/Feb/20
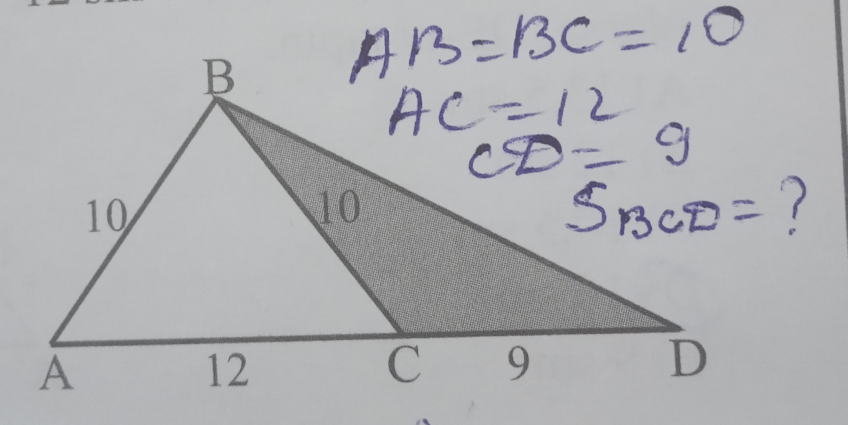
Commented by kaivan.ahmadi last updated on 02/Feb/20
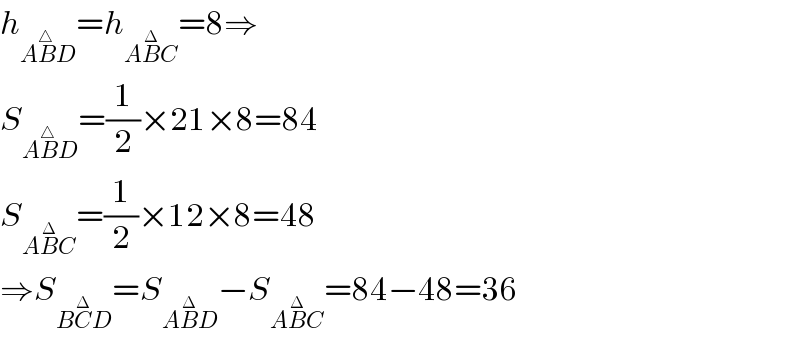
$${h}_{{A}\overset{\bigtriangleup} {{B}D}} ={h}_{{A}\overset{\Delta} {{B}C}} =\mathrm{8}\Rightarrow \\ $$$${S}_{{A}\overset{\bigtriangleup} {{B}D}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{21}×\mathrm{8}=\mathrm{84} \\ $$$${S}_{{A}\overset{\Delta} {{B}C}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{12}×\mathrm{8}=\mathrm{48} \\ $$$$\Rightarrow{S}_{{B}\overset{\Delta} {{C}D}} ={S}_{{A}\overset{\Delta} {{B}D}} −{S}_{{A}\overset{\Delta} {{B}C}} =\mathrm{84}−\mathrm{48}=\mathrm{36} \\ $$
Commented by gny last updated on 02/Feb/20
$${thank}\:{you}\:{so}\:{so}\:{much}\:{sir} \\ $$$${you}\:{are}\:{really}\:{perfect} \\ $$
Answered by sandy_delta last updated on 03/Feb/20
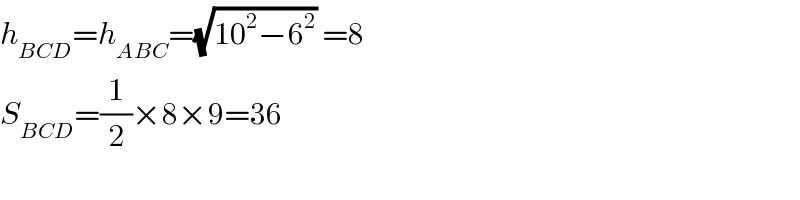
$${h}_{{BCD}} ={h}_{{ABC}} =\sqrt{\mathrm{10}^{\mathrm{2}} −\mathrm{6}^{\mathrm{2}} }\:=\mathrm{8} \\ $$$${S}_{{BCD}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{8}×\mathrm{9}=\mathrm{36} \\ $$
