Menu Close

Question-80432

Tinku Tara 0 Comments
Pin




Question Number 80432 by Power last updated on 03/Feb/20
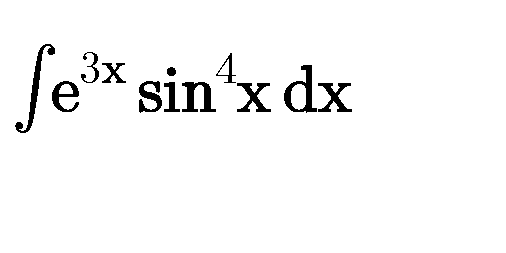
Commented by mr W last updated on 03/Feb/20
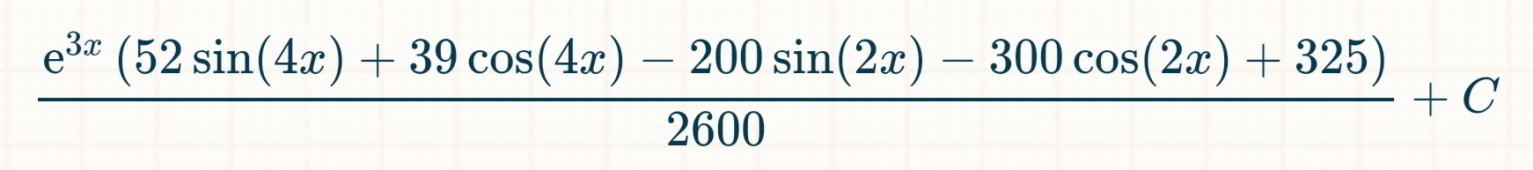
Commented by john santu last updated on 03/Feb/20
very small sir. haha
$${very}\:{small}\:{sir}.\:{haha} \\ $$
Commented by Power last updated on 03/Feb/20
solution sir
$$\mathrm{solution}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 03/Feb/20
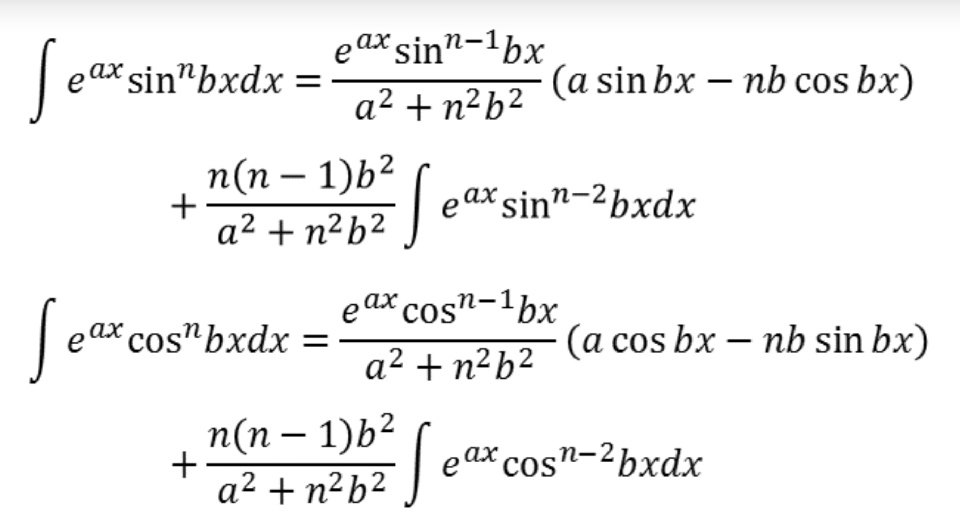
Commented by abdomathmax last updated on 03/Feb/20
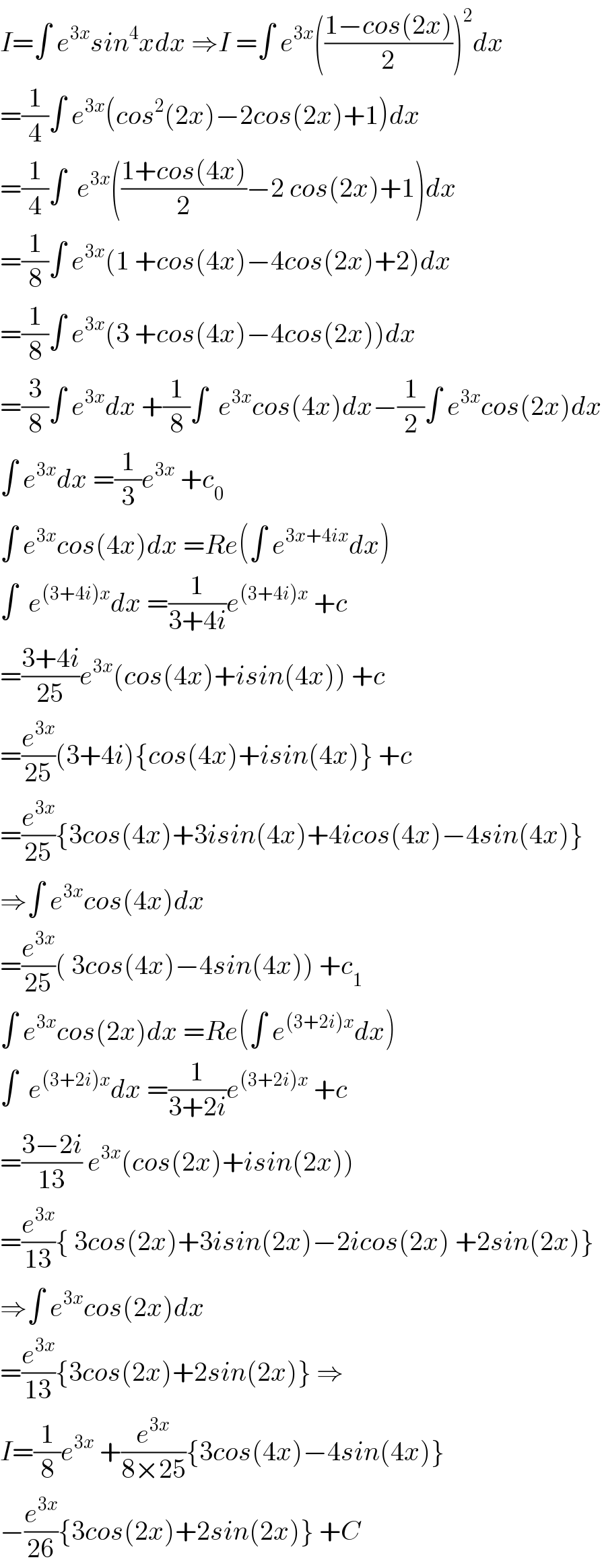
I=∫ e^(3x) sin^4 xdx ⇒I =∫ e^(3x) (((1−cos(2x))/2))^2 dx =(1/4)∫ e^(3x) (cos^2 (2x)−2cos(2x)+1)dx =(1/4)∫ e^(3x) (((1+cos(4x))/2)−2 cos(2x)+1)dx =(1/8)∫ e^(3x) (1 +cos(4x)−4cos(2x)+2)dx =(1/8)∫ e^(3x) (3 +cos(4x)−4cos(2x))dx =(3/8)∫ e^(3x) dx +(1/8)∫ e^(3x) cos(4x)dx−(1/2)∫ e^(3x) cos(2x)dx ∫ e^(3x) dx =(1/3)e^(3x) +c_0 ∫ e^(3x) cos(4x)dx =Re(∫ e^(3x+4ix) dx) ∫ e^((3+4i)x) dx =(1/(3+4i))e^((3+4i)x) +c =((3+4i)/(25))e^(3x) (cos(4x)+isin(4x)) +c =(e^(3x) /(25))(3+4i){cos(4x)+isin(4x)} +c =(e^(3x) /(25)){3cos(4x)+3isin(4x)+4icos(4x)−4sin(4x)} ⇒∫ e^(3x) cos(4x)dx =(e^(3x) /(25))( 3cos(4x)−4sin(4x)) +c_1 ∫ e^(3x) cos(2x)dx =Re(∫ e^((3+2i)x) dx) ∫ e^((3+2i)x) dx =(1/(3+2i))e^((3+2i)x) +c =((3−2i)/(13)) e^(3x) (cos(2x)+isin(2x)) =(e^(3x) /(13)){ 3cos(2x)+3isin(2x)−2icos(2x) +2sin(2x)} ⇒∫ e^(3x) cos(2x)dx =(e^(3x) /(13)){3cos(2x)+2sin(2x)} ⇒ I=(1/8)e^(3x) +(e^(3x) /(8×25)){3cos(4x)−4sin(4x)} −(e^(3x) /(26)){3cos(2x)+2sin(2x)} +C
$${I}=\int\:{e}^{\mathrm{3}{x}} {sin}^{\mathrm{4}} {xdx}\:\Rightarrow{I}\:=\int\:{e}^{\mathrm{3}{x}} \left(\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)^{\mathrm{2}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\:{e}^{\mathrm{3}{x}} \left({cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{2}{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:{e}^{\mathrm{3}{x}} \left(\frac{\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}−\mathrm{2}\:{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\:{e}^{\mathrm{3}{x}} \left(\mathrm{1}\:+{cos}\left(\mathrm{4}{x}\right)−\mathrm{4}{cos}\left(\mathrm{2}{x}\right)+\mathrm{2}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\:{e}^{\mathrm{3}{x}} \left(\mathrm{3}\:+{cos}\left(\mathrm{4}{x}\right)−\mathrm{4}{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\int\:{e}^{\mathrm{3}{x}} {dx}\:+\frac{\mathrm{1}}{\mathrm{8}}\int\:\:{e}^{\mathrm{3}{x}} {cos}\left(\mathrm{4}{x}\right){dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\:{e}^{\mathrm{3}{x}} {cos}\left(\mathrm{2}{x}\right){dx} \\ $$$$\int\:{e}^{\mathrm{3}{x}} {dx}\:=\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} \:+{c}_{\mathrm{0}} \\ $$$$\int\:{e}^{\mathrm{3}{x}} {cos}\left(\mathrm{4}{x}\right){dx}\:={Re}\left(\int\:{e}^{\mathrm{3}{x}+\mathrm{4}{ix}} {dx}\right) \\ $$$$\int\:\:{e}^{\left(\mathrm{3}+\mathrm{4}{i}\right){x}} {dx}\:=\frac{\mathrm{1}}{\mathrm{3}+\mathrm{4}{i}}{e}^{\left(\mathrm{3}+\mathrm{4}{i}\right){x}} \:+{c} \\ $$$$=\frac{\mathrm{3}+\mathrm{4}{i}}{\mathrm{25}}{e}^{\mathrm{3}{x}} \left({cos}\left(\mathrm{4}{x}\right)+{isin}\left(\mathrm{4}{x}\right)\right)\:+{c} \\ $$$$=\frac{{e}^{\mathrm{3}{x}} }{\mathrm{25}}\left(\mathrm{3}+\mathrm{4}{i}\right)\left\{{cos}\left(\mathrm{4}{x}\right)+{isin}\left(\mathrm{4}{x}\right)\right\}\:+{c} \\ $$$$=\frac{{e}^{\mathrm{3}{x}} }{\mathrm{25}}\left\{\mathrm{3}{cos}\left(\mathrm{4}{x}\right)+\mathrm{3}{isin}\left(\mathrm{4}{x}\right)+\mathrm{4}{icos}\left(\mathrm{4}{x}\right)−\mathrm{4}{sin}\left(\mathrm{4}{x}\right)\right\} \\ $$$$\Rightarrow\int\:{e}^{\mathrm{3}{x}} {cos}\left(\mathrm{4}{x}\right){dx} \\ $$$$=\frac{{e}^{\mathrm{3}{x}} }{\mathrm{25}}\left(\:\mathrm{3}{cos}\left(\mathrm{4}{x}\right)−\mathrm{4}{sin}\left(\mathrm{4}{x}\right)\right)\:+{c}_{\mathrm{1}} \\ $$$$\int\:{e}^{\mathrm{3}{x}} {cos}\left(\mathrm{2}{x}\right){dx}\:={Re}\left(\int\:{e}^{\left(\mathrm{3}+\mathrm{2}{i}\right){x}} {dx}\right) \\ $$$$\int\:\:{e}^{\left(\mathrm{3}+\mathrm{2}{i}\right){x}} {dx}\:=\frac{\mathrm{1}}{\mathrm{3}+\mathrm{2}{i}}{e}^{\left(\mathrm{3}+\mathrm{2}{i}\right){x}} \:+{c} \\ $$$$=\frac{\mathrm{3}−\mathrm{2}{i}}{\mathrm{13}}\:{e}^{\mathrm{3}{x}} \left({cos}\left(\mathrm{2}{x}\right)+{isin}\left(\mathrm{2}{x}\right)\right) \\ $$$$=\frac{{e}^{\mathrm{3}{x}} }{\mathrm{13}}\left\{\:\mathrm{3}{cos}\left(\mathrm{2}{x}\right)+\mathrm{3}{isin}\left(\mathrm{2}{x}\right)−\mathrm{2}{icos}\left(\mathrm{2}{x}\right)\:+\mathrm{2}{sin}\left(\mathrm{2}{x}\right)\right\} \\ $$$$\Rightarrow\int\:{e}^{\mathrm{3}{x}} {cos}\left(\mathrm{2}{x}\right){dx} \\ $$$$=\frac{{e}^{\mathrm{3}{x}} }{\mathrm{13}}\left\{\mathrm{3}{cos}\left(\mathrm{2}{x}\right)+\mathrm{2}{sin}\left(\mathrm{2}{x}\right)\right\}\:\Rightarrow \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{8}}{e}^{\mathrm{3}{x}} \:+\frac{{e}^{\mathrm{3}{x}} }{\mathrm{8}×\mathrm{25}}\left\{\mathrm{3}{cos}\left(\mathrm{4}{x}\right)−\mathrm{4}{sin}\left(\mathrm{4}{x}\right)\right\} \\ $$$$−\frac{{e}^{\mathrm{3}{x}} }{\mathrm{26}}\left\{\mathrm{3}{cos}\left(\mathrm{2}{x}\right)+\mathrm{2}{sin}\left(\mathrm{2}{x}\right)\right\}\:+{C} \\ $$
Commented by Power last updated on 03/Feb/20
thanks
$$\mathrm{thanks} \\ $$
Commented by Tony Lin last updated on 03/Feb/20
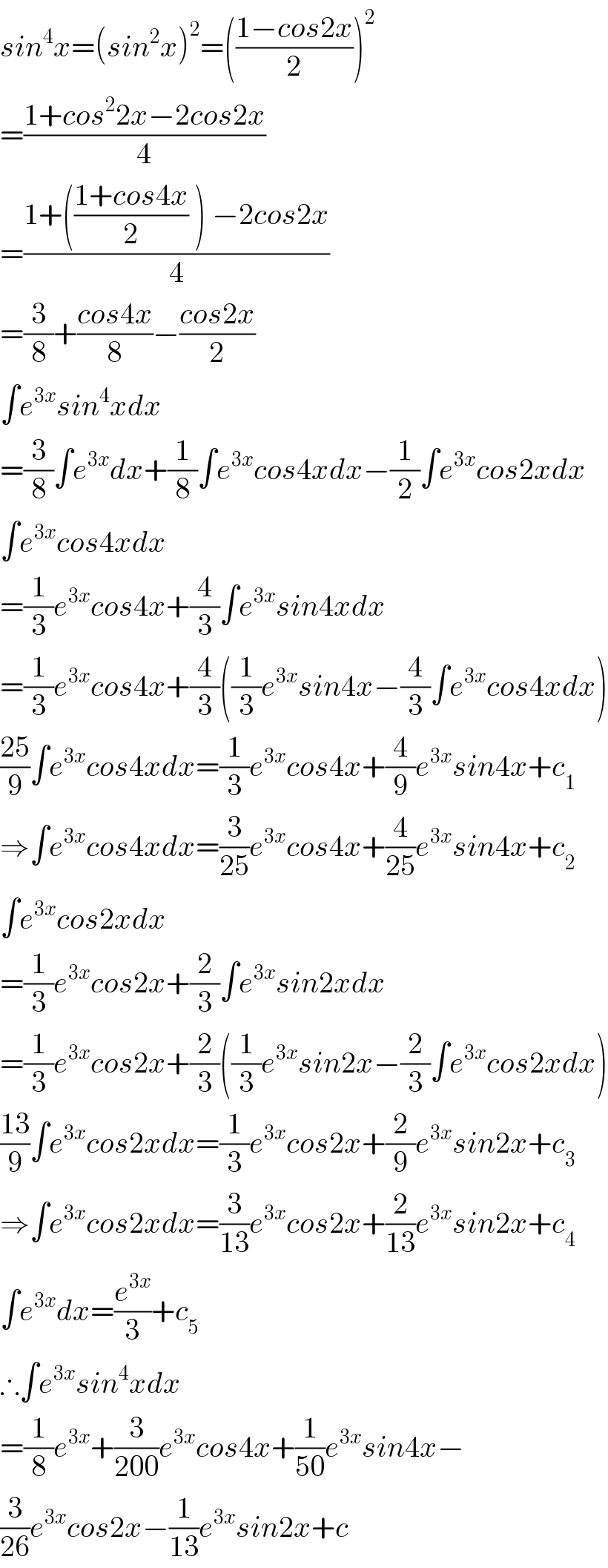
sin^4 x=(sin^2 x)^2 =(((1−cos2x)/2))^2 =((1+cos^2 2x−2cos2x)/4) =((1+(((1+cos4x)/2) ) −2cos2x)/4) =(3/8)+((cos4x)/8)−((cos2x)/2) ∫e^(3x) sin^4 xdx =(3/8)∫e^(3x) dx+(1/8)∫e^(3x) cos4xdx−(1/2)∫e^(3x) cos2xdx ∫e^(3x) cos4xdx =(1/3)e^(3x) cos4x+(4/3)∫e^(3x) sin4xdx =(1/3)e^(3x) cos4x+(4/3)((1/3)e^(3x) sin4x−(4/3)∫e^(3x) cos4xdx) ((25)/9)∫e^(3x) cos4xdx=(1/3)e^(3x) cos4x+(4/9)e^(3x) sin4x+c_1 ⇒∫e^(3x) cos4xdx=(3/(25))e^(3x) cos4x+(4/(25))e^(3x) sin4x+c_2 ∫e^(3x) cos2xdx =(1/3)e^(3x) cos2x+(2/3)∫e^(3x) sin2xdx =(1/3)e^(3x) cos2x+(2/3)((1/3)e^(3x) sin2x−(2/3)∫e^(3x) cos2xdx) ((13)/9)∫e^(3x) cos2xdx=(1/3)e^(3x) cos2x+(2/9)e^(3x) sin2x+c_3 ⇒∫e^(3x) cos2xdx=(3/(13))e^(3x) cos2x+(2/(13))e^(3x) sin2x+c_4 ∫e^(3x) dx=(e^(3x) /3)+c_5 ∴∫e^(3x) sin^4 xdx =(1/8)e^(3x) +(3/(200))e^(3x) cos4x+(1/(50))e^(3x) sin4x− (3/(26))e^(3x) cos2x−(1/(13))e^(3x) sin2x+c
$${sin}^{\mathrm{4}} {x}=\left({sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}+{cos}^{\mathrm{2}} \mathrm{2}{x}−\mathrm{2}{cos}\mathrm{2}{x}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}+\left(\frac{\mathrm{1}+{cos}\mathrm{4}{x}}{\mathrm{2}}\:\right)\:−\mathrm{2}{cos}\mathrm{2}{x}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}+\frac{{cos}\mathrm{4}{x}}{\mathrm{8}}−\frac{{cos}\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\int{e}^{\mathrm{3}{x}} {sin}^{\mathrm{4}} {xdx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\int{e}^{\mathrm{3}{x}} {dx}+\frac{\mathrm{1}}{\mathrm{8}}\int{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{xdx}−\frac{\mathrm{1}}{\mathrm{2}}\int{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{xdx} \\ $$$$\int{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{x}+\frac{\mathrm{4}}{\mathrm{3}}\int{e}^{\mathrm{3}{x}} {sin}\mathrm{4}{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{x}+\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} {sin}\mathrm{4}{x}−\frac{\mathrm{4}}{\mathrm{3}}\int{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{xdx}\right) \\ $$$$\frac{\mathrm{25}}{\mathrm{9}}\int{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{xdx}=\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{x}+\frac{\mathrm{4}}{\mathrm{9}}{e}^{\mathrm{3}{x}} {sin}\mathrm{4}{x}+{c}_{\mathrm{1}} \\ $$$$\Rightarrow\int{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{xdx}=\frac{\mathrm{3}}{\mathrm{25}}{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{x}+\frac{\mathrm{4}}{\mathrm{25}}{e}^{\mathrm{3}{x}} {sin}\mathrm{4}{x}+{c}_{\mathrm{2}} \\ $$$$\int{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{x}+\frac{\mathrm{2}}{\mathrm{3}}\int{e}^{\mathrm{3}{x}} {sin}\mathrm{2}{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{x}+\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} {sin}\mathrm{2}{x}−\frac{\mathrm{2}}{\mathrm{3}}\int{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{xdx}\right) \\ $$$$\frac{\mathrm{13}}{\mathrm{9}}\int{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{xdx}=\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{x}+\frac{\mathrm{2}}{\mathrm{9}}{e}^{\mathrm{3}{x}} {sin}\mathrm{2}{x}+{c}_{\mathrm{3}} \\ $$$$\Rightarrow\int{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{xdx}=\frac{\mathrm{3}}{\mathrm{13}}{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{x}+\frac{\mathrm{2}}{\mathrm{13}}{e}^{\mathrm{3}{x}} {sin}\mathrm{2}{x}+{c}_{\mathrm{4}} \\ $$$$\int{e}^{\mathrm{3}{x}} {dx}=\frac{{e}^{\mathrm{3}{x}} }{\mathrm{3}}+{c}_{\mathrm{5}} \\ $$$$\therefore\int{e}^{\mathrm{3}{x}} {sin}^{\mathrm{4}} {xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}{e}^{\mathrm{3}{x}} +\frac{\mathrm{3}}{\mathrm{200}}{e}^{\mathrm{3}{x}} {cos}\mathrm{4}{x}+\frac{\mathrm{1}}{\mathrm{50}}{e}^{\mathrm{3}{x}} {sin}\mathrm{4}{x}− \\ $$$$\frac{\mathrm{3}}{\mathrm{26}}{e}^{\mathrm{3}{x}} {cos}\mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{13}}{e}^{\mathrm{3}{x}} {sin}\mathrm{2}{x}+{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *