Question Number 80587 by ajfour last updated on 04/Feb/20

Commented by ajfour last updated on 04/Feb/20

$${Given}:\:\bigtriangleup{ABC}\:{is}\:{equilateral}, \\ $$$${radius}\:{of}\:{small}\:{circle}\:{is}\:\mathrm{1}. \\ $$$${Find}\:{radius}\:{of}\:{outer}\:{circle},\:{a}. \\ $$
Commented by ajfour last updated on 04/Feb/20

$${mrW}\:{Sir},\:{MjS}\:{Sir},\:{please}\:{attempt}.. \\ $$
Commented by mr W last updated on 04/Feb/20

$${i}\:{think}\:{if}\:{only}\:{the}\:{radius}\:{of}\:{the}\:{small} \\ $$$${circle}\:{is}\:{given},\:{the}\:{answer}\:{is}\:{not} \\ $$$${unique}.\:{see}\:{examples}:\:{both}\:{red}\:{and} \\ $$$${green}\:{circles}\:{satisfy}\:{the}\:{condition}. \\ $$
Commented by mr W last updated on 04/Feb/20

Commented by ajfour last updated on 04/Feb/20
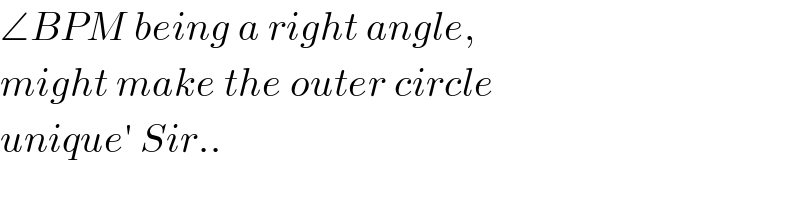
$$\angle{BPM}\:{being}\:{a}\:{right}\:{angle}, \\ $$$${might}\:{make}\:{the}\:{outer}\:{circle} \\ $$$${unique}'\:{Sir}.. \\ $$
Commented by mr W last updated on 04/Feb/20

$${then}\:{the}\:{solution}\:{is}\:{unique},\:{i}\:{think}. \\ $$
Answered by ajfour last updated on 04/Feb/20

Commented by ajfour last updated on 04/Feb/20

$$\mathrm{tan}\:\alpha=\frac{{a}−\mathrm{1}}{{a}}\:\:\:,\:\:\:{a}\mathrm{sec}\:\alpha=\mathrm{2} \\ $$$$\Rightarrow\:\:\mathrm{1}+\left(\frac{{a}−\mathrm{1}}{{a}}\right)^{\mathrm{2}} =\frac{\mathrm{4}}{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{a}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\:\:{a}=\frac{\mathrm{1}+\sqrt{\mathrm{7}}}{\mathrm{2}}\:. \\ $$$$ \\ $$
Commented by mr W last updated on 04/Feb/20

$${nice}\:{diagram}\:{and}\:{solution}\:{sir}! \\ $$$${we}\:{can}\:{also}\:{get} \\ $$$$\left({a}−\mathrm{1}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{a}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}+\sqrt{\mathrm{7}}}{\mathrm{2}} \\ $$
