Question Number 80595 by Power last updated on 04/Feb/20
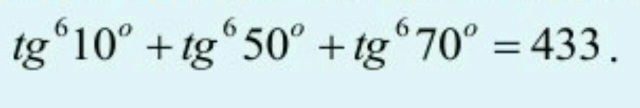
Commented by Power last updated on 04/Feb/20

$$\mathrm{prove}\:\mathrm{that} \\ $$
Commented by Power last updated on 04/Feb/20

$$\mathrm{sir}\:\mathrm{W}\:\mathrm{pls} \\ $$
Answered by mind is power last updated on 05/Feb/20
$${my}\:{idee}\:{start} \\ $$$${withe} \\ $$$${tg}\left(\mathrm{3}.\mathrm{10}\right)={tg}\left(\mathrm{30}\right),{tg}\left(\mathrm{3}.\mathrm{50}\right)={tg}\left(\mathrm{150}\right)={tg}\left(\mathrm{180}−\mathrm{30}\right)=−{tg}\left(\mathrm{30}\right) \\ $$$${tg}\left(\mathrm{3}.\mathrm{70}\right)={tg}\left(\mathrm{210}\right)={tg}\left(\mathrm{180}+\mathrm{30}\right)={tg}\left(\mathrm{30}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow−{tg}\left(\mathrm{50}\right),{tg}\left(\mathrm{10}\right),{tg}\left(\mathrm{70}\right)\:{Root}\:{of}\:{Somm}\:{polynomial}\:{in}\:{tan}\left({a}\right) \\ $$$${tan}\left(\mathrm{3}{a}\right)=\frac{{tan}\left({a}\right)+{tan}\left(\mathrm{2}{a}\right)}{\mathrm{1}−{tan}\left({a}\right){tan}\left(\mathrm{2}{a}\right)} \\ $$$${tan}\left(\mathrm{2}{a}\right)=\frac{\mathrm{2}{tan}\left({a}\right)}{\mathrm{1}−{tan}^{\mathrm{2}} \left({a}\right)}\Rightarrow{tan}\left(\mathrm{3}{a}\right)=\frac{\mathrm{3}{tan}\left({a}\right)−{tan}^{\mathrm{3}} \left({a}\right)}{\mathrm{1}−\mathrm{3}{tan}^{\mathrm{2}} \left({a}\right)} \\ $$$$\left(−{tan}\left(\mathrm{50}\right),{tan}\left(\mathrm{10}\right),{tan}\left(\mathrm{70}\right)\right)\:{Root}\:{of} \\ $$$$\frac{\mathrm{3}{X}−{X}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{X}^{\mathrm{2}} }=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\Leftrightarrow{X}^{\mathrm{3}} −\sqrt{\mathrm{3}}{X}−\mathrm{3}{X}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\mathrm{0} \\ $$$${a}={tan}\left(\mathrm{10}\right),{b}={tan}\left(\mathrm{70}\right),{c}=−{tan}\left(\mathrm{50}\right) \\ $$$${Viet}\:{identities}\Rightarrow \\ $$$${a}+{b}+{c}=\sqrt{\mathrm{3}}={e}_{\mathrm{1}} \\ $$$${e}_{\mathrm{2}} ={ab}+{bc}+{ca}=−\mathrm{3} \\ $$$${e}_{\mathrm{3}} ={abc}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}},{e}_{{n}} =\mathrm{0},\forall{n}\geqslant\mathrm{4} \\ $$$${we}\:{use}\:{newtoon}\:{identities} \\ $$$${let}\:{p}_{{k}} ={a}^{{k}} +{b}^{{k}} +{c}^{{k}} \\ $$$${p}_{\mathrm{1}} ={e}_{\mathrm{1}} =\sqrt{\mathrm{3}} \\ $$$${p}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −\mathrm{2}{e}_{\mathrm{2}} =\mathrm{9} \\ $$$${p}_{\mathrm{3}} ={e}_{\mathrm{1}} {p}_{\mathrm{2}} −{e}_{\mathrm{2}} {p}_{\mathrm{1}} +\mathrm{3}{e}_{\mathrm{3}} =\mathrm{11}\sqrt{\mathrm{3}} \\ $$$${p}_{\mathrm{4}} ={e}_{\mathrm{1}} {p}_{\mathrm{3}} −{e}_{\mathrm{2}} {p}_{\mathrm{2}} +{e}_{\mathrm{3}} {p}_{\mathrm{1}} =\mathrm{59} \\ $$$${p}_{\mathrm{5}} ={e}_{\mathrm{1}} {p}_{\mathrm{4}} −{e}_{\mathrm{2}} {p}_{\mathrm{3}} +{e}_{\mathrm{3}} {p}_{\mathrm{2}} =\mathrm{89}\sqrt{\mathrm{5}} \\ $$$${p}_{\mathrm{6}} ={e}_{\mathrm{1}} {p}_{\mathrm{5}} −{e}_{\mathrm{2}} {p}_{\mathrm{4}} +{e}_{\mathrm{3}} {p}_{\mathrm{3}} =\mathrm{89}\sqrt{\mathrm{3}}.\sqrt{\mathrm{3}}+\mathrm{3}.\mathrm{59}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}.\mathrm{11}\sqrt{\mathrm{3}}=\mathrm{433} \\ $$$${p}_{\mathrm{6}} ={a}^{\mathrm{6}} +{b}^{\mathrm{6}} +{c}^{\mathrm{6}} ={tg}^{\mathrm{6}} \left(\mathrm{10}\right)+\left(−{tg}\left(\mathrm{50}\right)\right)^{\mathrm{6}} +{tg}^{\mathrm{6}} \left(\mathrm{70}\right)=\mathrm{433} \\ $$$$={tg}^{\mathrm{6}} \left(\mathrm{10}\right)+{tg}^{\mathrm{6}} \left(\mathrm{50}\right)+{tg}^{\mathrm{6}} \left(\mathrm{70}\right)=\mathrm{433}\:\:{We}\:{get}\:{our}\:{results} \\ $$$$ \\ $$$$ \\ $$
Commented by Power last updated on 05/Feb/20

$$\boldsymbol{\mathrm{thank}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{sir}}.\:\boldsymbol{\mathrm{Great}}! \\ $$
Commented by mind is power last updated on 05/Feb/20

$${withe}\:{pleasur} \\ $$
