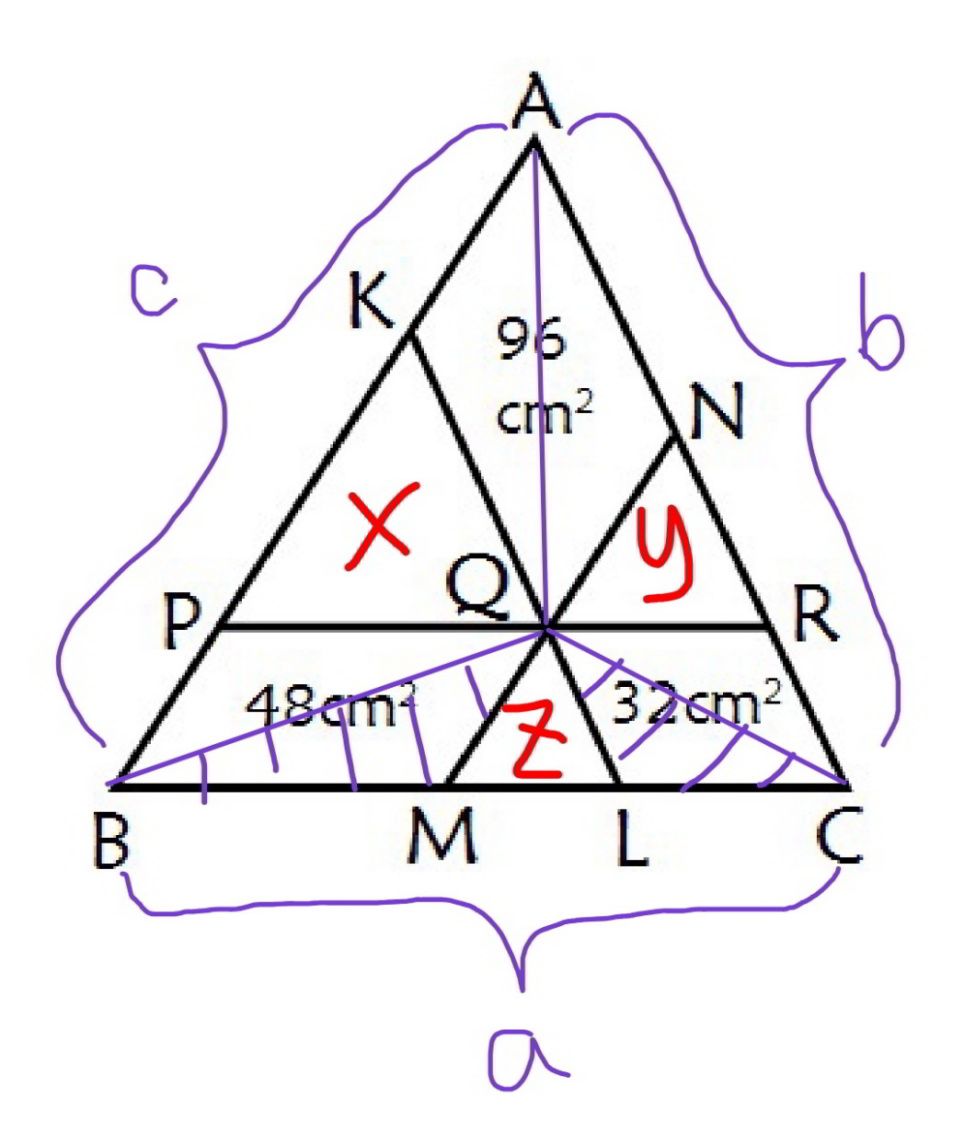
Question Number 80675 by naka3546 last updated on 05/Feb/20
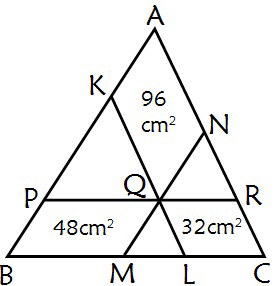
Commented by naka3546 last updated on 05/Feb/20
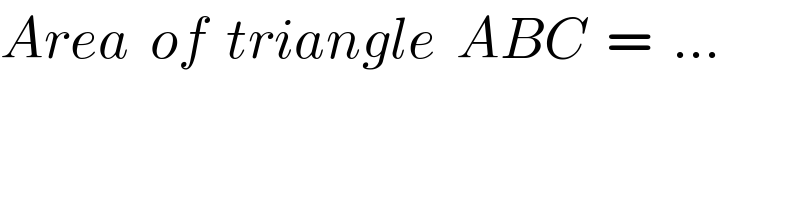
$${Area}\:\:{of}\:\:{triangle}\:\:{ABC}\:\:=\:\:… \\ $$
Answered by mr W last updated on 05/Feb/20
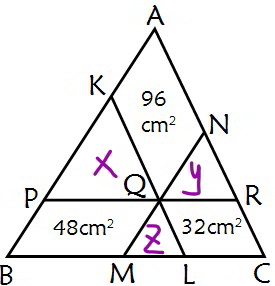
Commented by mr W last updated on 05/Feb/20
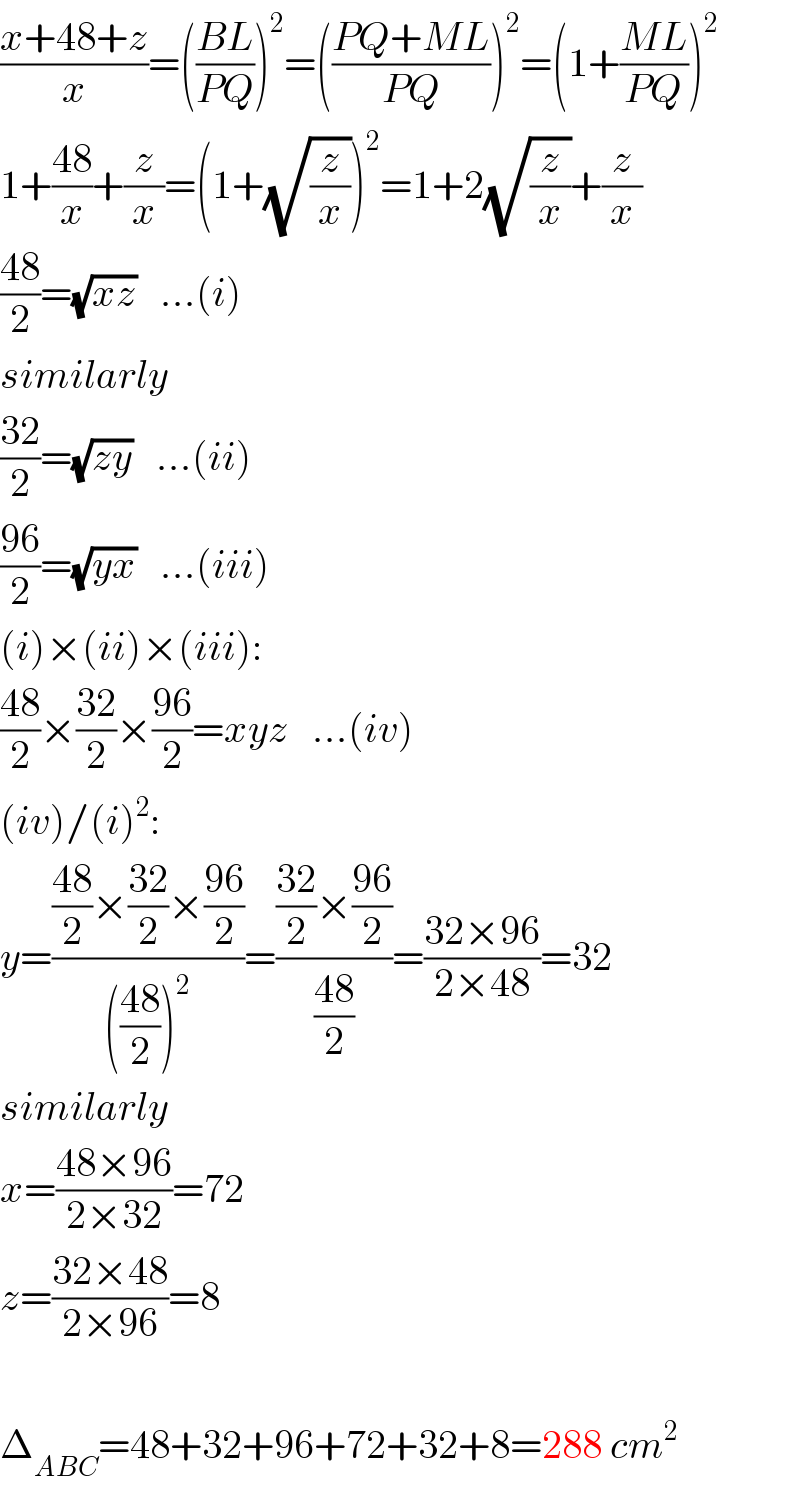
$$\frac{{x}+\mathrm{48}+{z}}{{x}}=\left(\frac{{BL}}{{PQ}}\right)^{\mathrm{2}} =\left(\frac{{PQ}+{ML}}{{PQ}}\right)^{\mathrm{2}} =\left(\mathrm{1}+\frac{{ML}}{{PQ}}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}+\frac{\mathrm{48}}{{x}}+\frac{{z}}{{x}}=\left(\mathrm{1}+\sqrt{\frac{{z}}{{x}}}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{2}\sqrt{\frac{{z}}{{x}}}+\frac{{z}}{{x}} \\ $$$$\frac{\mathrm{48}}{\mathrm{2}}=\sqrt{{xz}}\:\:\:…\left({i}\right) \\ $$$${similarly} \\ $$$$\frac{\mathrm{32}}{\mathrm{2}}=\sqrt{{zy}}\:\:\:…\left({ii}\right) \\ $$$$\frac{\mathrm{96}}{\mathrm{2}}=\sqrt{{yx}}\:\:\:…\left({iii}\right) \\ $$$$\left({i}\right)×\left({ii}\right)×\left({iii}\right): \\ $$$$\frac{\mathrm{48}}{\mathrm{2}}×\frac{\mathrm{32}}{\mathrm{2}}×\frac{\mathrm{96}}{\mathrm{2}}={xyz}\:\:\:…\left({iv}\right) \\ $$$$\left({iv}\right)/\left({i}\right)^{\mathrm{2}} : \\ $$$${y}=\frac{\frac{\mathrm{48}}{\mathrm{2}}×\frac{\mathrm{32}}{\mathrm{2}}×\frac{\mathrm{96}}{\mathrm{2}}}{\left(\frac{\mathrm{48}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\frac{\mathrm{32}}{\mathrm{2}}×\frac{\mathrm{96}}{\mathrm{2}}}{\frac{\mathrm{48}}{\mathrm{2}}}=\frac{\mathrm{32}×\mathrm{96}}{\mathrm{2}×\mathrm{48}}=\mathrm{32} \\ $$$${similarly} \\ $$$${x}=\frac{\mathrm{48}×\mathrm{96}}{\mathrm{2}×\mathrm{32}}=\mathrm{72} \\ $$$${z}=\frac{\mathrm{32}×\mathrm{48}}{\mathrm{2}×\mathrm{96}}=\mathrm{8} \\ $$$$ \\ $$$$\Delta_{{ABC}} =\mathrm{48}+\mathrm{32}+\mathrm{96}+\mathrm{72}+\mathrm{32}+\mathrm{8}=\mathrm{288}\:{cm}^{\mathrm{2}} \\ $$
Answered by mr W last updated on 05/Feb/20