Question Number 80682 by ajfour last updated on 05/Feb/20

Commented by ajfour last updated on 05/Feb/20

$${If}\:{both}\:{coloured}\:{areas}\:{are}\:{equal}, \\ $$$${find}\:{r}. \\ $$
Commented by ajfour last updated on 05/Feb/20

$${fine}\:{sir},\:{thanks};\:{i}\:{shall}\:{try}\:{and} \\ $$$${check}\:{my}\:{answer}\:{with}\:{yours}, \\ $$$${only}\:{problem},\:{my}\:{calculator} \\ $$$${is}\:{not}\:{reliable}.. \\ $$
Commented by MJS last updated on 05/Feb/20
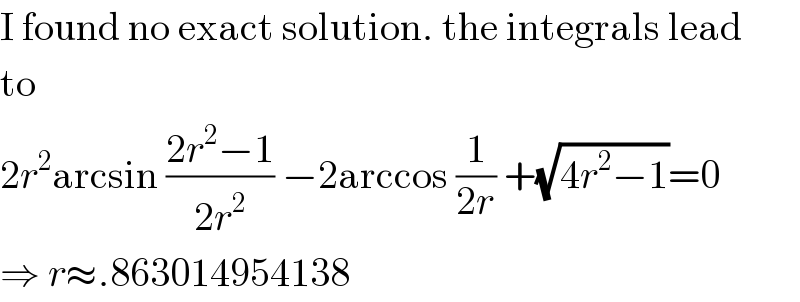
$$\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{exact}\:\mathrm{solution}.\:\mathrm{the}\:\mathrm{integrals}\:\mathrm{lead} \\ $$$$\mathrm{to} \\ $$$$\mathrm{2}{r}^{\mathrm{2}} \mathrm{arcsin}\:\frac{\mathrm{2}{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{r}^{\mathrm{2}} }\:−\mathrm{2arccos}\:\frac{\mathrm{1}}{\mathrm{2}{r}}\:+\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\mathrm{1}}=\mathrm{0} \\ $$$$\Rightarrow\:{r}\approx.\mathrm{863014954138} \\ $$
