Question Number 80687 by Power last updated on 05/Feb/20
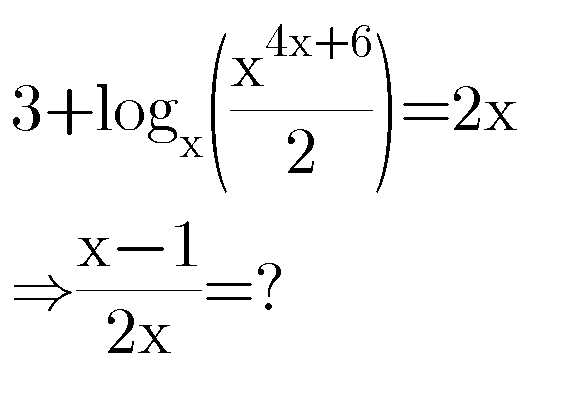
Commented by Power last updated on 05/Feb/20
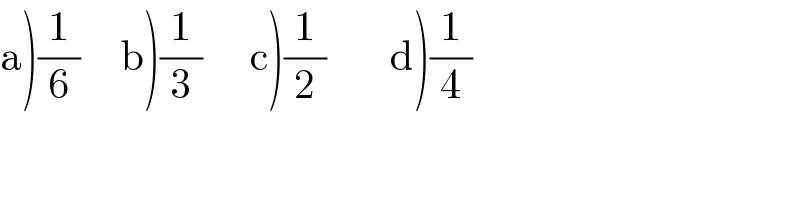
$$\left.\mathrm{a}\left.\right)\left.\frac{\mathrm{1}}{\mathrm{6}}\left.\:\:\:\:\:\mathrm{b}\right)\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:\mathrm{c}\right)\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\mathrm{d}\right)\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by MJS last updated on 05/Feb/20
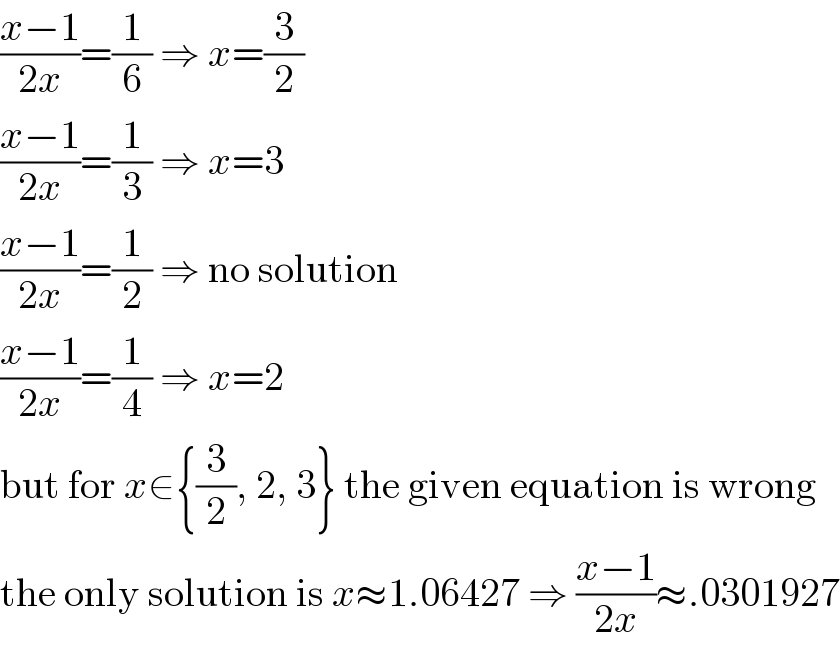
$$\frac{{x}−\mathrm{1}}{\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow\:{x}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\frac{{x}−\mathrm{1}}{\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:{x}=\mathrm{3} \\ $$$$\frac{{x}−\mathrm{1}}{\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\frac{{x}−\mathrm{1}}{\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:{x}=\mathrm{2} \\ $$$$\mathrm{but}\:\mathrm{for}\:{x}\in\left\{\frac{\mathrm{3}}{\mathrm{2}},\:\mathrm{2},\:\mathrm{3}\right\}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is}\:{x}\approx\mathrm{1}.\mathrm{06427}\:\Rightarrow\:\frac{{x}−\mathrm{1}}{\mathrm{2}{x}}\approx.\mathrm{0301927} \\ $$
