Question Number 80786 by M±th+et£s last updated on 06/Feb/20

Commented by mind is power last updated on 06/Feb/20

$${i}\:{will}\:{try}\:{not}\:{easy}\:! \\ $$
Commented by mr W last updated on 06/Feb/20
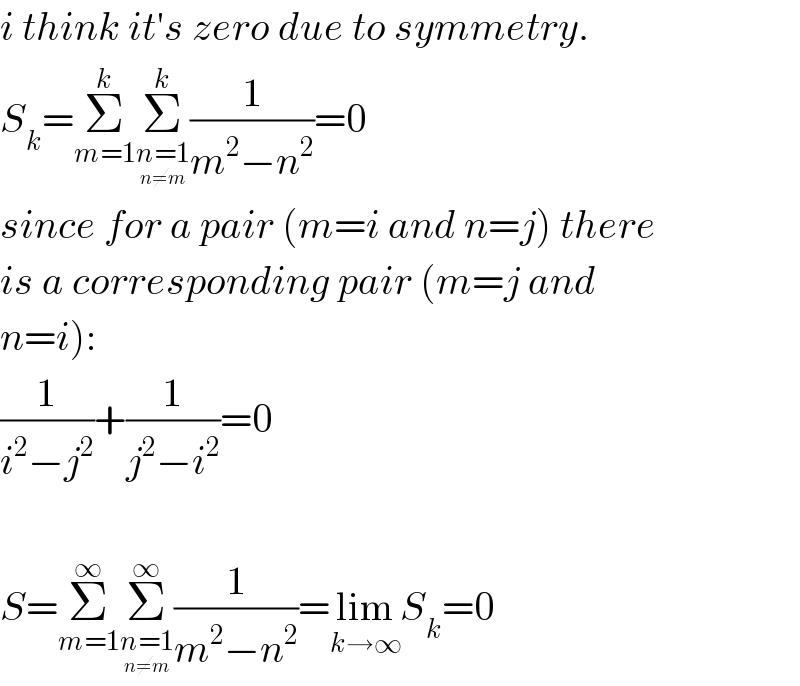
$${i}\:{think}\:{it}'{s}\:{zero}\:{due}\:{to}\:{symmetry}. \\ $$$${S}_{{k}} =\underset{{m}=\mathrm{1}} {\overset{{k}} {\sum}}\underset{\underset{{n}\neq{m}} {{n}=\mathrm{1}}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }=\mathrm{0} \\ $$$${since}\:{for}\:{a}\:{pair}\:\left({m}={i}\:{and}\:{n}={j}\right)\:{there} \\ $$$${is}\:{a}\:{corresponding}\:{pair}\:\left({m}={j}\:{and}\right. \\ $$$$\left.{n}={i}\right): \\ $$$$\frac{\mathrm{1}}{{i}^{\mathrm{2}} −{j}^{\mathrm{2}} }+\frac{\mathrm{1}}{{j}^{\mathrm{2}} −{i}^{\mathrm{2}} }=\mathrm{0} \\ $$$$ \\ $$$${S}=\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{\underset{{n}\neq{m}} {{n}=\mathrm{1}}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }=\underset{{k}\rightarrow\infty} {\mathrm{lim}}{S}_{{k}} =\mathrm{0} \\ $$
Commented by mr W last updated on 06/Feb/20
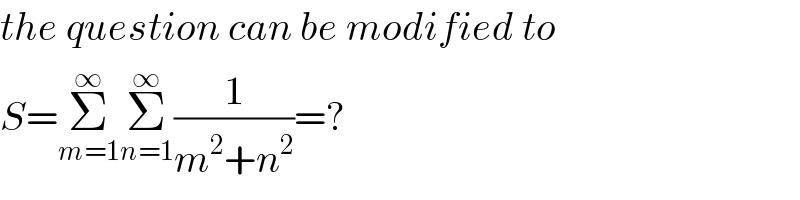
$${the}\:{question}\:{can}\:{be}\:{modified}\:{to} \\ $$$${S}=\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }=? \\ $$
Commented by mathmax by abdo last updated on 06/Feb/20
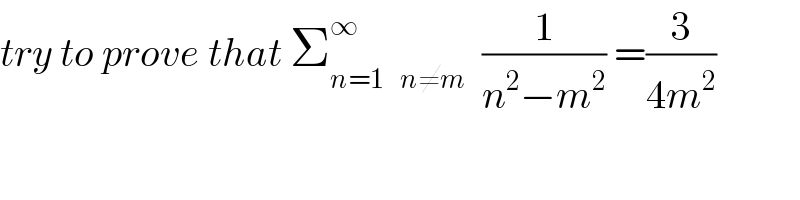
$${try}\:{to}\:{prove}\:{that}\:\sum_{{n}=\mathrm{1}\:\:\:\:{n}\neq{m}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} −{m}^{\mathrm{2}} }\:=\frac{\mathrm{3}}{\mathrm{4}{m}^{\mathrm{2}} } \\ $$
Commented by ~blr237~ last updated on 07/Feb/20

$${let}\:{h}\left({m}\right)=\underset{{n}\in\mathbb{N}} {\sum}\:\frac{\mathrm{1}}{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }\: \\ $$$${let}\:{state}\:{f}\left({z}\right)=\frac{\mathrm{1}}{{m}^{\mathrm{2}} +{z}^{\mathrm{2}} }\:,\:{using}\:{the}\:{Residu}\:{theorem} \\ $$$${h}\left({m}\right)=−\Sigma{Res}\left({f}\left({z}\right)\pi{cot}\left(\pi{z}\right),{z}_{{k}} \right)\: \\ $$$${h}\left({m}\right)=−\left(\:\frac{\pi{cot}\left({i}\pi{m}\right)}{\mathrm{2}{im}}\:+\frac{\pi{cot}\left(−{i}\pi{m}\right)}{−\mathrm{2}{im}}\right) \\ $$$${h}\left({m}\right)={i}\pi\frac{{cot}\left({i}\pi{m}\right)}{{m}}\:=\frac{\pi{coth}\left(\pi{m}\right)}{{m}}\: \\ $$$${So}\:\:,\:{S}=\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\:+\frac{\pi{coth}\left(\pi{m}\right)}{\mathrm{2}{m}}\right) \\ $$$${S}=\zeta\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{2}}\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{coth}\left(\pi{m}\right)}{{m}}\: \\ $$$$ \\ $$
Answered by ~blr237~ last updated on 07/Feb/20
![We have ∀ m≥2 Σ_(n=_(n≠m) 1) ^∞ (1/(m^2 −n^2 )) =− (3/(4m^2 )) (let prove) f(m)=Σ_(n=1 n≠m) ^∞ (1/(m^2 −n^2 )) . knowing (1/(m^2 −n^2 )) =−(1/(2m))((1/(n−m))−(1/(n+m))) f(m)= −(1/(2m)) [Σ_(n=1) ^(m−1) ((1/(n−m))−(1/(n+m)))+Σ_(n=m+1) ^∞ ((1/(n−m))−(1/(n+m)))] f(m)=(1/(2m))[ Σ_(p=m+1) ^(2m−1) (1/p) +Σ_(p=1) ^(m−1) (1/p)]−(1/(2m))[Σ_(p=1) ^∞ ((1/p)−(1/(p+2m)))] let show that g(m)=Σ_(p=1) ^∞ ((1/p)−(1/(p+m)))=Σ_(p=1) ^m (1/p) g(m)=Σ_(p=1) ^∞ (Σ_(k=0) ^(m−1) ((1/(p+k))−(1/(p+k+1)))) =Σ_(k=0) ^(m−1) (Σ_(p=1) ^∞ ((1/(k+p))−(1/(k+p+1)))) =Σ_(k=0) ^(m−1) (1/(k+1))=Σ_(k=1) ^m (1/k) So , f(m)=(1/(2m))(Σ_(p=1) ^(2m−1) (1/p) −(1/m))−(1/(2m))Σ_(p=1) ^(2m) (1/p) f(m)=−(1/(2m^2 )) −(1/(2m))×(1/(2m)) =−(3/(4m^2 )) Finally S=Σ_(m=1) ^∞ f(m)=−(3/4)ζ(2)=−(π^2 /8)](https://www.tinkutara.com/question/Q80826.png)
$${We}\:{have}\:\forall\:{m}\geqslant\mathrm{2}\:\:\:\:\underset{{n}\underset{{n}\neq{m}} {=}\mathrm{1}} {\overset{\infty} {\sum}}\:\:\frac{\mathrm{1}}{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }\:=−\:\frac{\mathrm{3}}{\mathrm{4}{m}^{\mathrm{2}} }\:\:\:\:\:\left({let}\:{prove}\right)\: \\ $$$${f}\left({m}\right)=\underset{{n}=\mathrm{1}\:\:{n}\neq{m}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }\:\:\:.\:\:{knowing}\:\frac{\mathrm{1}}{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{2}{m}}\left(\frac{\mathrm{1}}{{n}−{m}}−\frac{\mathrm{1}}{{n}+{m}}\right) \\ $$$$\:\:{f}\left({m}\right)=\:−\frac{\mathrm{1}}{\mathrm{2}{m}}\:\left[\underset{{n}=\mathrm{1}} {\overset{{m}−\mathrm{1}} {\sum}}\left(\frac{\mathrm{1}}{{n}−{m}}−\frac{\mathrm{1}}{{n}+{m}}\right)+\underset{{n}={m}+\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}−{m}}−\frac{\mathrm{1}}{{n}+{m}}\right)\right] \\ $$$${f}\left({m}\right)=\frac{\mathrm{1}}{\mathrm{2}{m}}\left[\:\underset{{p}={m}+\mathrm{1}} {\overset{\mathrm{2}{m}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{p}}\:+\underset{{p}=\mathrm{1}} {\overset{{m}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{p}}\right]−\frac{\mathrm{1}}{\mathrm{2}{m}}\left[\underset{{p}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{p}}−\frac{\mathrm{1}}{{p}+\mathrm{2}{m}}\right)\right]\:\: \\ $$$${let}\:{show}\:{that}\:\:{g}\left({m}\right)=\underset{{p}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{p}}−\frac{\mathrm{1}}{{p}+{m}}\right)=\underset{{p}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\mathrm{1}}{{p}} \\ $$$${g}\left({m}\right)=\underset{{p}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\underset{{k}=\mathrm{0}} {\overset{{m}−\mathrm{1}} {\sum}}\left(\frac{\mathrm{1}}{{p}+{k}}−\frac{\mathrm{1}}{{p}+{k}+\mathrm{1}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{{m}−\mathrm{1}} {\sum}}\left(\underset{{p}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}+{p}}−\frac{\mathrm{1}}{{k}+{p}+\mathrm{1}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{{m}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{1}}=\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\:\frac{\mathrm{1}}{{k}}\: \\ $$$${So}\:, \\ $$$${f}\left({m}\right)=\frac{\mathrm{1}}{\mathrm{2}{m}}\left(\underset{{p}=\mathrm{1}} {\overset{\mathrm{2}{m}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{p}}\:−\frac{\mathrm{1}}{{m}}\right)−\frac{\mathrm{1}}{\mathrm{2}{m}}\underset{{p}=\mathrm{1}} {\overset{\mathrm{2}{m}} {\sum}}\frac{\mathrm{1}}{{p}}\: \\ $$$${f}\left({m}\right)=−\frac{\mathrm{1}}{\mathrm{2}{m}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}{m}}×\frac{\mathrm{1}}{\mathrm{2}{m}}\:=−\frac{\mathrm{3}}{\mathrm{4}{m}^{\mathrm{2}} }\: \\ $$$${Finally}\:\:{S}=\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}{f}\left({m}\right)=−\frac{\mathrm{3}}{\mathrm{4}}\zeta\left(\mathrm{2}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\: \\ $$
Commented by M±th+et£s last updated on 07/Feb/20
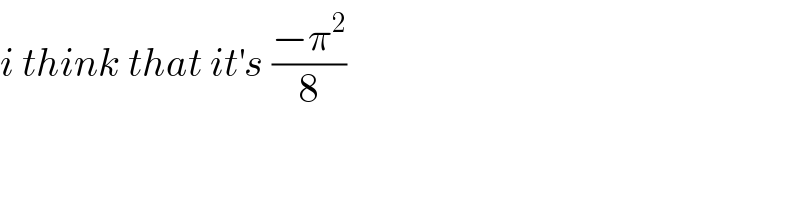
$${i}\:{think}\:{that}\:{it}^{'} {s}\:\frac{−\pi^{\mathrm{2}} }{\mathrm{8}}\: \\ $$
Commented by ~blr237~ last updated on 07/Feb/20

$${yes}\:{it}'{s} \\ $$
Commented by M±th+et£s last updated on 07/Feb/20
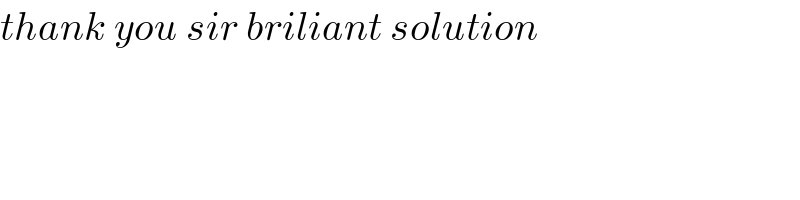
$${thank}\:{you}\:{sir}\:{briliant}\:{solution} \\ $$
