Question Number 80795 by mr W last updated on 06/Feb/20

Commented by mr W last updated on 06/Feb/20

$${Find}\:{the}\:{equation}\:{of}\:{the}\:{parabola},\:{i}.{e}. \\ $$$${the}\:{value}\:{k}\:{as}\:{well}\:{as}\:{the}\:{corresponding} \\ $$$${coordinates}\:{of}\:{points}\:{A},{B},{C}\:{such}\:{that} \\ $$$${the}\:{areas}\:{I},\:{II},\:{III},\:{IV}\:\:{are}\:{equal}. \\ $$
Commented by MJS last updated on 06/Feb/20
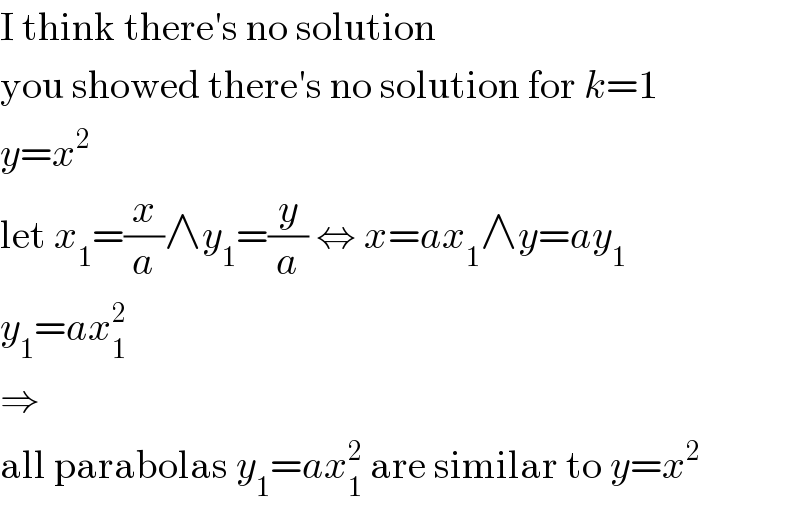
$$\mathrm{I}\:\mathrm{think}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{you}\:\mathrm{showed}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:{k}=\mathrm{1} \\ $$$${y}={x}^{\mathrm{2}} \\ $$$$\mathrm{let}\:{x}_{\mathrm{1}} =\frac{{x}}{{a}}\wedge{y}_{\mathrm{1}} =\frac{{y}}{{a}}\:\Leftrightarrow\:{x}={ax}_{\mathrm{1}} \wedge{y}={ay}_{\mathrm{1}} \\ $$$${y}_{\mathrm{1}} ={ax}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{all}\:\mathrm{parabolas}\:{y}_{\mathrm{1}} ={ax}_{\mathrm{1}} ^{\mathrm{2}} \:\mathrm{are}\:\mathrm{similar}\:\mathrm{to}\:{y}={x}^{\mathrm{2}} \\ $$
Commented by mr W last updated on 07/Feb/20

$${you}\:{are}\:{right}\:{sir}! \\ $$
