Menu Close

Question-80809

Tinku Tara 0 Comments
Pin




Question Number 80809 by mr W last updated on 06/Feb/20
Commented by mr W last updated on 06/Feb/20
I is a point inside the triangle ABC. P,Q,R are the midpoint of AI,BI,CI respectively. What fraction of the triangle ABC does the shaded hexagon present?
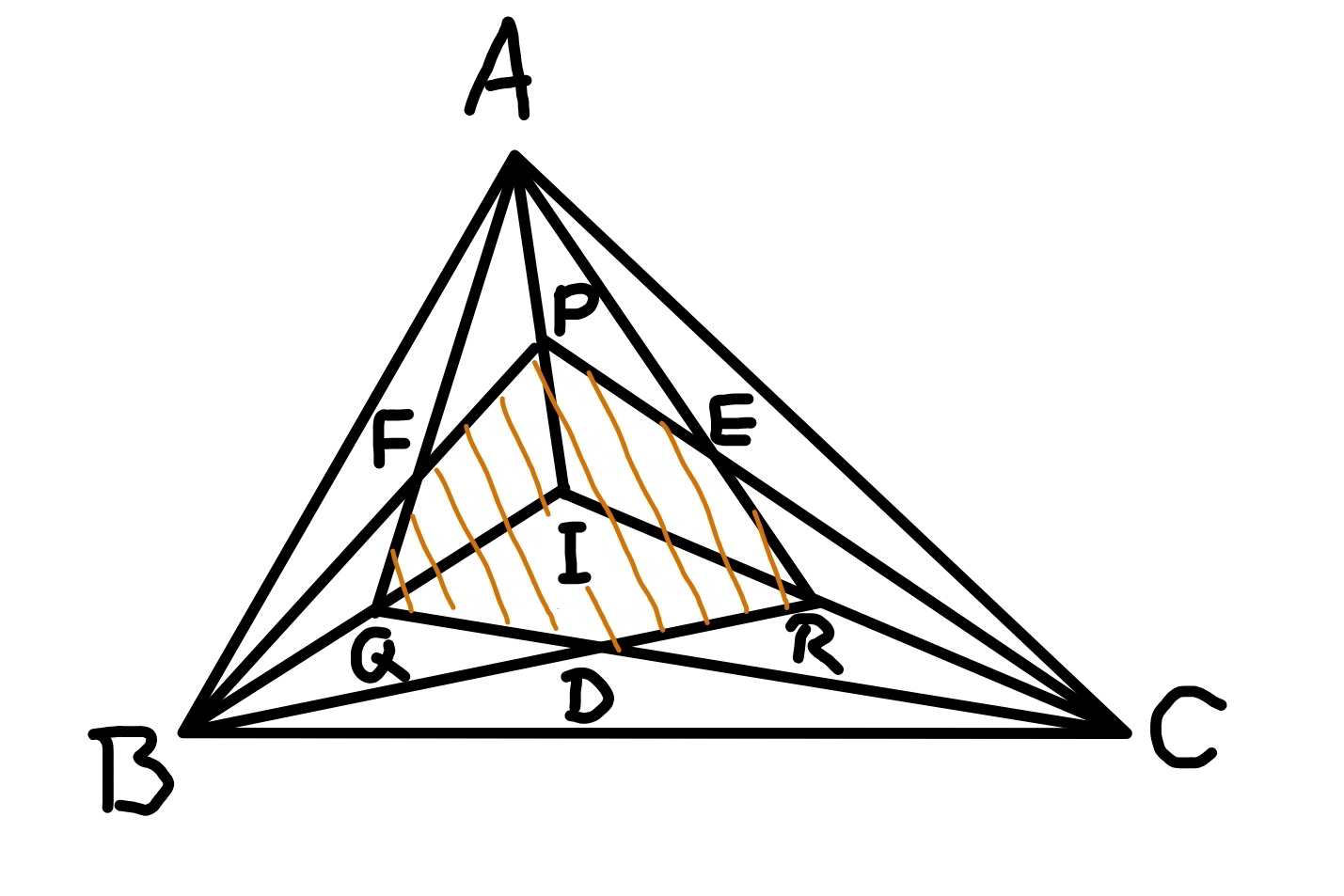
$${I}\:{is}\:{a}\:{point}\:{inside}\:{the}\:{triangle}\:{ABC}. \\ $$$${P},{Q},{R}\:{are}\:{the}\:{midpoint}\:{of}\:{AI},{BI},{CI} \\ $$$${respectively}. \\ $$$${What}\:{fraction}\:{of}\:{the}\:{triangle}\:{ABC} \\ $$$${does}\:{the}\:{shaded}\:{hexagon}\:{present}? \\ $$
Commented by ajfour last updated on 07/Feb/20
Commented by ajfour last updated on 07/Feb/20
△_(ABC) =Σ2qrsin α eq. of AR: v^� =r^� +λ(2p^� −r^� ) eq. of CP: v^� =p^� +μ(2r^� −p^� ) v_E ^� = r^� +λ(2p^� −r^� )=p^� +μ(2r^� −p^� ) ⇒ 1−λ=2μ , 2λ=1−μ ⇒ 1−λ=2−4λ ⇒ λ=1/3 v_E ^� = r^� +((2p^� −r^� )/3) = (2/3)(p^� +r^� ) A_(IREP) =prsin β((4/9)+(1/9)+(1/9)) = (2/3)prsin β A_(hexagon) =(2/3)Σprsin β hence (A_(hexagon) /△_(ABC) )=((2/3)/2) = (1/3) .
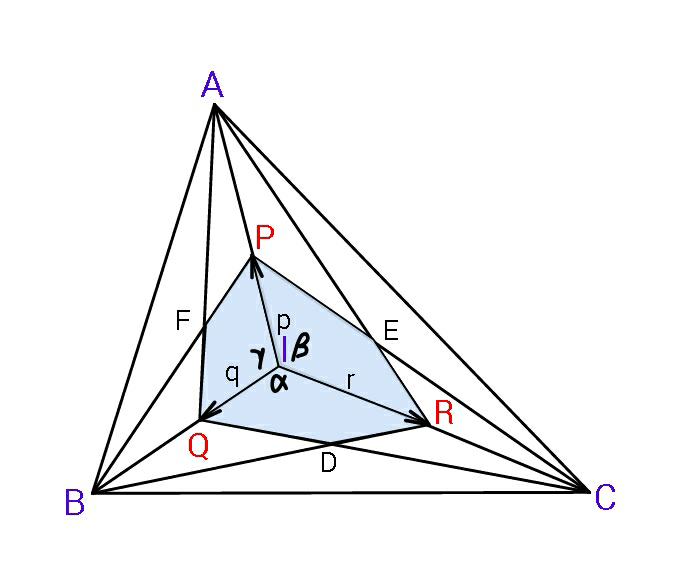
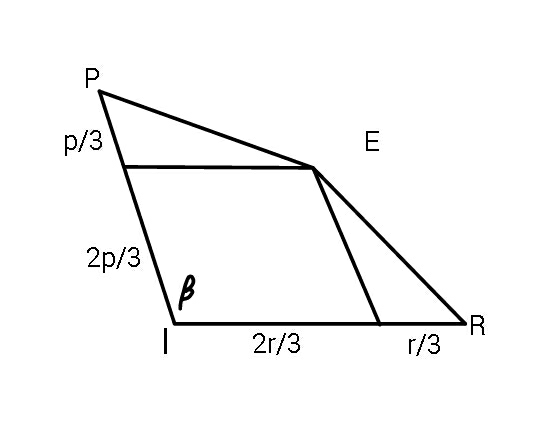
$$\bigtriangleup_{{ABC}} =\Sigma\mathrm{2}{qr}\mathrm{sin}\:\alpha \\ $$$${eq}.\:{of}\:{AR}:\:\:\:\:\bar {{v}}=\bar {{r}}+\lambda\left(\mathrm{2}\bar {{p}}−\bar {{r}}\right) \\ $$$${eq}.\:{of}\:{CP}:\:\:\:\:\:\bar {{v}}=\bar {{p}}+\mu\left(\mathrm{2}\bar {{r}}−\bar {{p}}\right) \\ $$$$\bar {{v}}_{{E}} =\:\bar {{r}}+\lambda\left(\mathrm{2}\bar {{p}}−\bar {{r}}\right)=\bar {{p}}+\mu\left(\mathrm{2}\bar {{r}}−\bar {{p}}\right) \\ $$$$\Rightarrow\:\:\mathrm{1}−\lambda=\mathrm{2}\mu\:\:,\:\:\mathrm{2}\lambda=\mathrm{1}−\mu \\ $$$$\Rightarrow\:\:\:\mathrm{1}−\lambda=\mathrm{2}−\mathrm{4}\lambda\:\:\:\Rightarrow\:\lambda=\mathrm{1}/\mathrm{3} \\ $$$$\bar {{v}}_{{E}} =\:\bar {{r}}+\frac{\mathrm{2}\bar {{p}}−\bar {{r}}}{\mathrm{3}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\left(\bar {{p}}+\bar {{r}}\right) \\ $$$${A}_{{IREP}} ={pr}\mathrm{sin}\:\beta\left(\frac{\mathrm{4}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{9}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2}}{\mathrm{3}}{pr}\mathrm{sin}\:\beta \\ $$$${A}_{{hexagon}} =\frac{\mathrm{2}}{\mathrm{3}}\Sigma{pr}\mathrm{sin}\:\beta \\ $$$${hence}\:\:\:\:\frac{{A}_{{hexagon}} }{\bigtriangleup_{{ABC}} }=\frac{\mathrm{2}/\mathrm{3}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:. \\ $$$$ \\ $$
Commented by mr W last updated on 07/Feb/20
answer is correct! it′s a nice vector method sir!
$${answer}\:{is}\:{correct}! \\ $$$${it}'{s}\:{a}\:{nice}\:{vector}\:{method}\:{sir}! \\ $$
Commented by ajfour last updated on 07/Feb/20
Answered by mr W last updated on 07/Feb/20
Commented by mr W last updated on 07/Feb/20
an other way: as example we treat only the part ΔIBC. draw QN//BR NR=IN=((IR)/2)=((RC)/2) ⇒QD=((DC)/2) ΔQDB=((ΔDCB)/2)=((ΔQCB)/3)=((ΔIBC)/6) ΔRBC=((ΔIBC)/2) A_(IQDR) =ΔIBC−ΔRBC−ΔQDB A_(IQDR) =ΔIBC−((ΔIBC)/2)−((ΔIBC)/6)=((ΔIBC)/3) ΣA_(IQDR) =((ΣΔIBC)/3) ⇒hexagon =((ΔABC)/3)
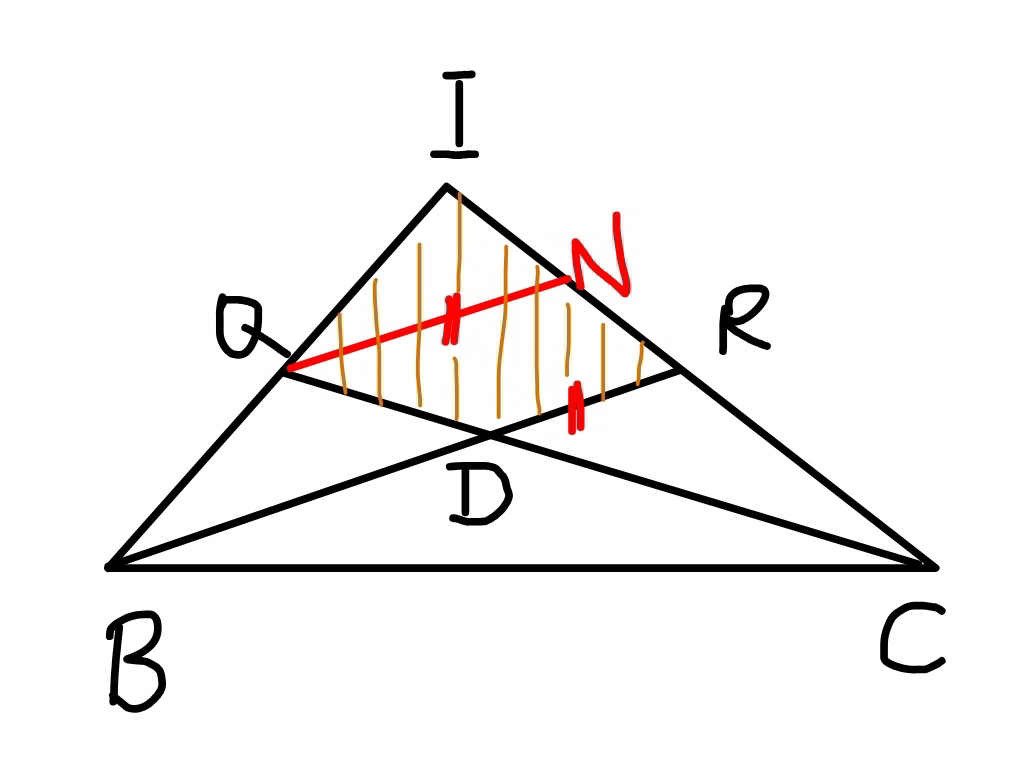
$${an}\:{other}\:{way}: \\ $$$${as}\:{example}\:{we}\:{treat}\:{only}\:{the}\:{part}\:\Delta{IBC}. \\ $$$${draw}\:{QN}//{BR} \\ $$$${NR}={IN}=\frac{{IR}}{\mathrm{2}}=\frac{{RC}}{\mathrm{2}} \\ $$$$\Rightarrow{QD}=\frac{{DC}}{\mathrm{2}} \\ $$$$\Delta{QDB}=\frac{\Delta{DCB}}{\mathrm{2}}=\frac{\Delta{QCB}}{\mathrm{3}}=\frac{\Delta{IBC}}{\mathrm{6}} \\ $$$$\Delta{RBC}=\frac{\Delta{IBC}}{\mathrm{2}} \\ $$$${A}_{{IQDR}} =\Delta{IBC}−\Delta{RBC}−\Delta{QDB} \\ $$$${A}_{{IQDR}} =\Delta{IBC}−\frac{\Delta{IBC}}{\mathrm{2}}−\frac{\Delta{IBC}}{\mathrm{6}}=\frac{\Delta{IBC}}{\mathrm{3}} \\ $$$$\Sigma{A}_{{IQDR}} =\frac{\Sigma\Delta{IBC}}{\mathrm{3}} \\ $$$$\Rightarrow{hexagon}\:=\frac{\Delta{ABC}}{\mathrm{3}} \\ $$
Commented by ajfour last updated on 07/Feb/20
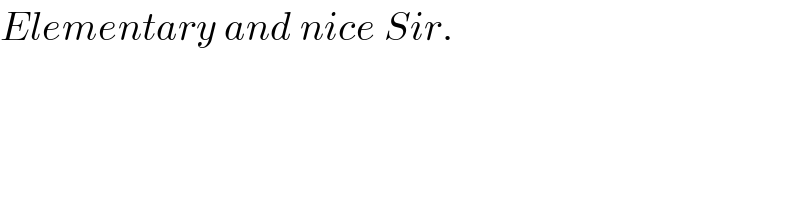
Elementary and nice Sir.
$${Elementary}\:{and}\:{nice}\:{Sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *