Question Number 80882 by mr W last updated on 07/Feb/20
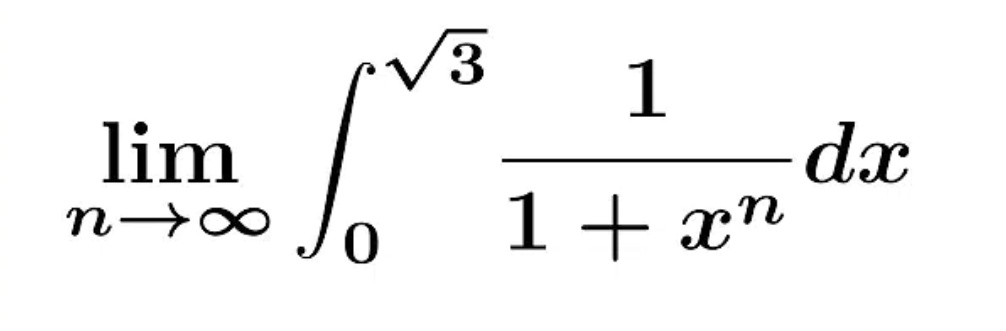
Commented by jagoll last updated on 07/Feb/20
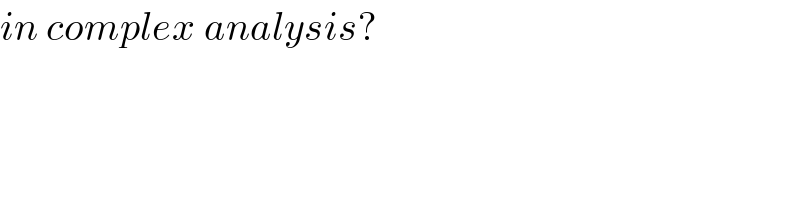
$${in}\:{complex}\:{analysis}? \\ $$
Commented by ajfour last updated on 07/Feb/20

$$=\mathrm{1}\:? \\ $$
Commented by mr W last updated on 07/Feb/20
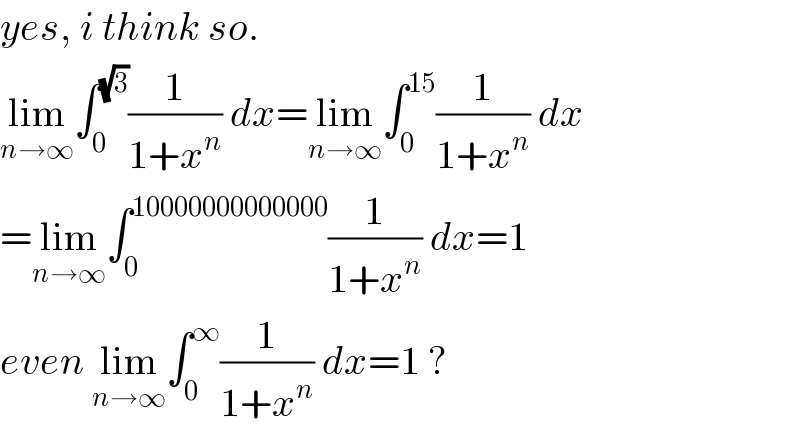
$${yes},\:{i}\:{think}\:{so}. \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:{dx}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{15}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:{dx} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{10000000000000}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:{dx}=\mathrm{1} \\ $$$${even}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:{dx}=\mathrm{1}\:? \\ $$
Commented by mathmax by abdo last updated on 07/Feb/20
![let I_n =∫_0 ^(√3) (dx/(1+x^n )) ⇒I_n =∫_R (1/(1+x^n )) χ_([0,(√(3]))) (x)dx =∫_R f_n (x)dx with f_n (x)=(1/(1+x^n )) χ_([0,(√3)]) (x)dx if 0≤x<1 f_n →χ_([0,(√3)]) (x)=1 ⇒lim_(n→+∞) I_n =(√3) if x>1 f_n →0 (s.c) and we have x^n >1 ⇒(1/(1+x^n ))χ_([0,(√3)]) (x)<(1/2)χ_([0,(√3)]) (x) theorem of convergence dominee give lim_(n→+∞) ∫_R f_n (x)dx =∫_R lim_(n→+∞) f_n (x)dx =0](https://www.tinkutara.com/question/Q80910.png)
$${let}\:{I}_{{n}} =\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \:\:\frac{{dx}}{\mathrm{1}+{x}^{{n}} }\:\Rightarrow{I}_{{n}} =\int_{{R}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:\chi_{\left[\mathrm{0},\sqrt{\left.\mathrm{3}\right]}\right.} \left({x}\right){dx}\:=\int_{{R}} {f}_{{n}} \left({x}\right){dx} \\ $$$${with}\:{f}_{{n}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:\chi_{\left[\mathrm{0},\sqrt{\mathrm{3}}\right]} \left({x}\right){dx} \\ $$$${if}\:\:\mathrm{0}\leqslant{x}<\mathrm{1}\:\:{f}_{{n}} \rightarrow\chi_{\left[\mathrm{0},\sqrt{\mathrm{3}}\right]} \:\left({x}\right)=\mathrm{1}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{I}_{{n}} =\sqrt{\mathrm{3}} \\ $$$${if}\:{x}>\mathrm{1}\:\:\:\:{f}_{{n}} \rightarrow\mathrm{0}\:\:\left({s}.{c}\right)\:\:{and}\:{we}\:{have}\:\:{x}^{{n}} >\mathrm{1}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\chi_{\left[\mathrm{0},\sqrt{\mathrm{3}}\right]} \left({x}\right)<\frac{\mathrm{1}}{\mathrm{2}}\chi_{\left[\mathrm{0},\sqrt{\mathrm{3}}\right]} \left({x}\right) \\ $$$${theorem}\:{of}\:{convergence}\:{dominee}\:{give}\: \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:\int_{{R}} {f}_{{n}} \left({x}\right){dx}\:=\int_{{R}} {lim}_{{n}\rightarrow+\infty} {f}_{{n}} \left({x}\right){dx}\:=\mathrm{0} \\ $$$$ \\ $$
Answered by ~blr237~ last updated on 07/Feb/20
![let g(a)= lim_(n→∞) ∫_0 ^a f_n (x) dx with f_n (x)=(1/(1+x^n )) ,a>0 we have ∀ x∈[0,a] 0<(a/(1+a^n ))≤∫_0 ^a (1/(1+x^n ))dx ≤ a so ∀ n f_n is integrable and (∫_0 ^a f_n (x)dx)_(n≥1) is confined if x∈[0,1] x^(n+1) ≤x^n and f_n (x)≤f_(n+1) (x) if x∈[1:∞[ x^n <x^(n+1) and f_(n+1) (x)≤f_n (x) then (f_n ) is monotone :so due to CSM lim_(n→∞) ∫_0 ^a f_n (x)dx=∫_0 ^a lim_(n→∞) f_n (x)dx= { ((∫_0 ^a 1dx if a<1)),((∫_0 ^1 1dx +∫_1 ^a 0dx if a≥1)) :}= { ((a if a<1)),((1 if a≥1)) :} lim_(n→∞) ∫_0 ^∞ (1/(1+x^n ))dx=lim_(a→∞) g(a) = 1](https://www.tinkutara.com/question/Q80905.png)
$${let}\:\:{g}\left({a}\right)=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\int_{\mathrm{0}} ^{{a}} \:{f}_{{n}} \left({x}\right)\:{dx}\:\:\:\:\:{with}\:{f}_{{n}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }\:\:\:,{a}>\mathrm{0} \\ $$$$\:{we}\:{have}\:\forall\:{x}\in\left[\mathrm{0},{a}\right]\:\:\:\mathrm{0}<\frac{{a}}{\mathrm{1}+{a}^{{n}} }\leqslant\int_{\mathrm{0}} ^{{a}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }{dx}\:\leqslant\:{a}\: \\ $$$${so}\:\forall\:{n}\:\:\:\:{f}_{{n}} \:{is}\:{integrable}\:{and}\:\:\left(\int_{\mathrm{0}} ^{{a}} {f}_{{n}} \left({x}\right){dx}\right)_{{n}\geqslant\mathrm{1}} {is}\:\:{confined}\: \\ $$$${if}\:\:\:\:{x}\in\left[\mathrm{0},\mathrm{1}\right]\:\:\:\:{x}^{{n}+\mathrm{1}} \leqslant{x}^{{n}} \:\:{and}\:\:\:{f}_{{n}} \left({x}\right)\leqslant{f}_{{n}+\mathrm{1}} \left({x}\right)\: \\ $$$${if}\:\:{x}\in\left[\mathrm{1}:\infty\left[\:\:\:\:\:\:{x}^{{n}} <{x}^{{n}+\mathrm{1}} \:\:{and}\:\:{f}_{{n}+\mathrm{1}} \left({x}\right)\leqslant{f}_{{n}} \left({x}\right)\right.\right. \\ $$$${then}\:\:\left({f}_{{n}} \right)\:{is}\:\:{monotone}\:\::{so}\:{due}\:{to}\:{CSM}\:\:\: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:\int_{\mathrm{0}} ^{{a}} {f}_{{n}} \left({x}\right){dx}=\int_{\mathrm{0}} ^{{a}} \underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:{f}_{{n}} \left({x}\right){dx}=\begin{cases}{\int_{\mathrm{0}} ^{{a}} \:\mathrm{1}{dx}\:\:{if}\:{a}<\mathrm{1}}\\{\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1}{dx}\:+\int_{\mathrm{1}} ^{{a}} \mathrm{0}{dx}\:\:{if}\:{a}\geqslant\mathrm{1}}\end{cases}=\begin{cases}{{a}\:\:\:{if}\:\:{a}<\mathrm{1}}\\{\mathrm{1}\:{if}\:\:{a}\geqslant\mathrm{1}}\end{cases} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{{n}} }{dx}=\underset{{a}\rightarrow\infty} {\mathrm{lim}}\:{g}\left({a}\right)\:=\:\mathrm{1}\: \\ $$
Commented by mr W last updated on 07/Feb/20

$${thanks}\:{alot}\:{sir}! \\ $$
