Question Number 80900 by ajfour last updated on 07/Feb/20
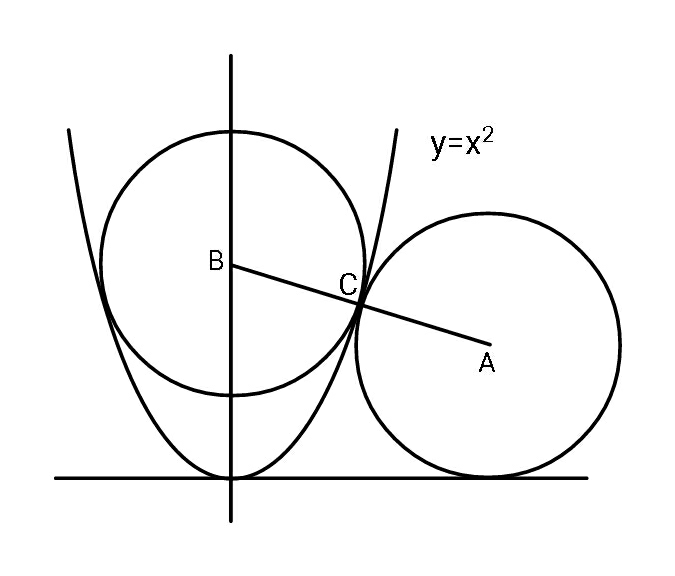
Commented by ajfour last updated on 07/Feb/20
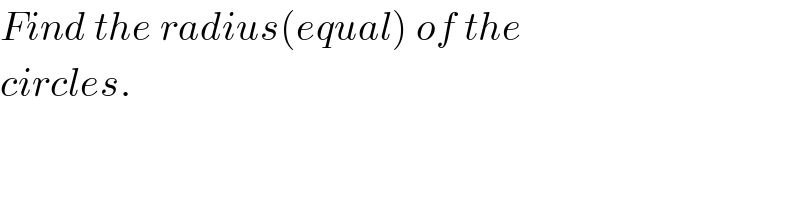
$${Find}\:{the}\:{radius}\left({equal}\right)\:{of}\:{the}\: \\ $$$${circles}. \\ $$
Answered by ajfour last updated on 07/Feb/20
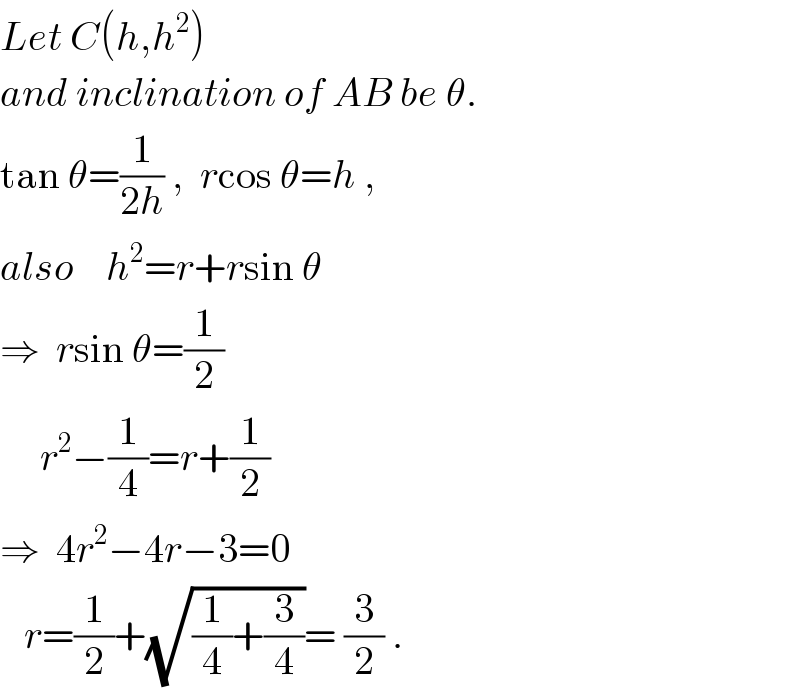
$${Let}\:{C}\left({h},{h}^{\mathrm{2}} \right) \\ $$$${and}\:{inclination}\:{of}\:{AB}\:{be}\:\theta. \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\mathrm{2}{h}}\:,\:\:{r}\mathrm{cos}\:\theta={h}\:, \\ $$$${also}\:\:\:\:{h}^{\mathrm{2}} ={r}+{r}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:{r}\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:{r}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}={r}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{4}{r}^{\mathrm{2}} −\mathrm{4}{r}−\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:{r}=\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}}=\:\frac{\mathrm{3}}{\mathrm{2}}\:. \\ $$
Commented by peter frank last updated on 08/Feb/20

$${please}\:{help}\:\mathrm{78652} \\ $$
Commented by mr W last updated on 08/Feb/20
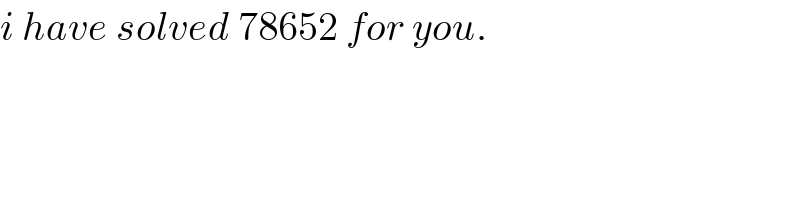
$${i}\:{have}\:{solved}\:\mathrm{78652}\:{for}\:{you}. \\ $$
Commented by peter frank last updated on 08/Feb/20
$${thank}\:{you}\:{sir}\:{mr}\:{w} \\ $$
