Question Number 80912 by TawaTawa last updated on 07/Feb/20
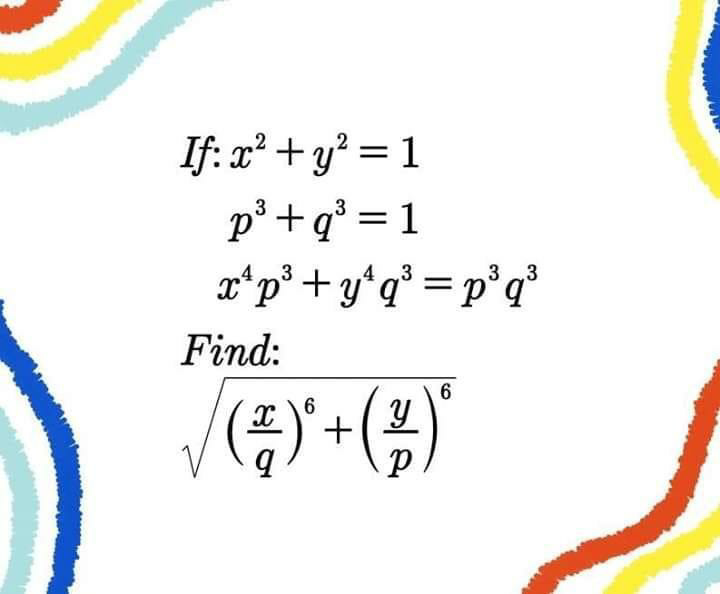
Commented by john santu last updated on 08/Feb/20
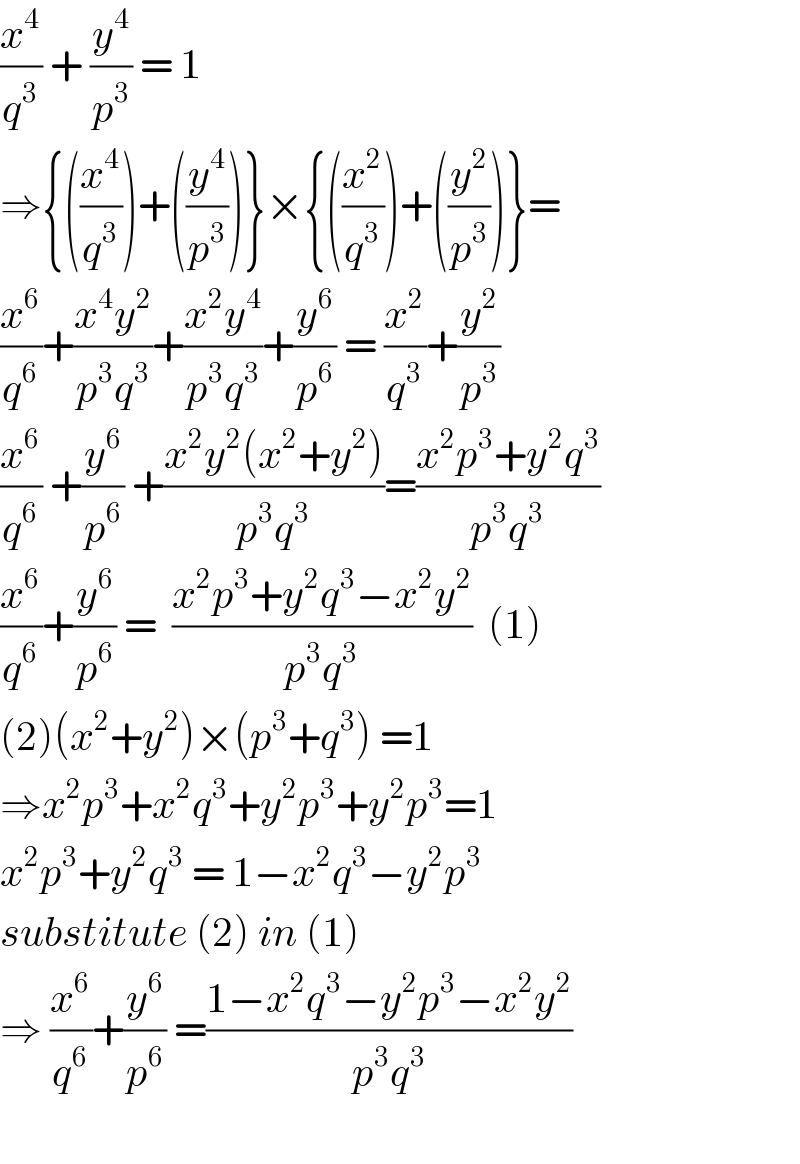
$$\frac{{x}^{\mathrm{4}} }{{q}^{\mathrm{3}} }\:+\:\frac{{y}^{\mathrm{4}} }{{p}^{\mathrm{3}} }\:=\:\mathrm{1}\: \\ $$$$\Rightarrow\left\{\left(\frac{{x}^{\mathrm{4}} }{{q}^{\mathrm{3}} }\right)+\left(\frac{{y}^{\mathrm{4}} }{{p}^{\mathrm{3}} }\right)\right\}×\left\{\left(\frac{{x}^{\mathrm{2}} }{{q}^{\mathrm{3}} }\right)+\left(\frac{{y}^{\mathrm{2}} }{{p}^{\mathrm{3}} }\right)\right\}= \\ $$$$\frac{{x}^{\mathrm{6}} }{{q}^{\mathrm{6}} }+\frac{{x}^{\mathrm{4}} {y}^{\mathrm{2}} }{{p}^{\mathrm{3}} {q}^{\mathrm{3}} }+\frac{{x}^{\mathrm{2}} {y}^{\mathrm{4}} }{{p}^{\mathrm{3}} {q}^{\mathrm{3}} }+\frac{{y}^{\mathrm{6}} }{{p}^{\mathrm{6}} }\:=\:\frac{{x}^{\mathrm{2}} }{{q}^{\mathrm{3}} }+\frac{{y}^{\mathrm{2}} }{{p}^{\mathrm{3}} } \\ $$$$\frac{{x}^{\mathrm{6}} }{{q}^{\mathrm{6}} }\:+\frac{{y}^{\mathrm{6}} }{{p}^{\mathrm{6}} }\:+\frac{{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}{{p}^{\mathrm{3}} {q}^{\mathrm{3}} }=\frac{{x}^{\mathrm{2}} {p}^{\mathrm{3}} +{y}^{\mathrm{2}} {q}^{\mathrm{3}} }{{p}^{\mathrm{3}} {q}^{\mathrm{3}} } \\ $$$$\frac{{x}^{\mathrm{6}} }{{q}^{\mathrm{6}} }+\frac{{y}^{\mathrm{6}} }{{p}^{\mathrm{6}} }\:=\:\:\frac{{x}^{\mathrm{2}} {p}^{\mathrm{3}} +{y}^{\mathrm{2}} {q}^{\mathrm{3}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} }{{p}^{\mathrm{3}} {q}^{\mathrm{3}} }\:\:\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)×\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)\:=\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} {p}^{\mathrm{3}} +{x}^{\mathrm{2}} {q}^{\mathrm{3}} +{y}^{\mathrm{2}} {p}^{\mathrm{3}} +{y}^{\mathrm{2}} {p}^{\mathrm{3}} =\mathrm{1} \\ $$$${x}^{\mathrm{2}} {p}^{\mathrm{3}} +{y}^{\mathrm{2}} {q}^{\mathrm{3}} \:=\:\mathrm{1}−{x}^{\mathrm{2}} {q}^{\mathrm{3}} −{y}^{\mathrm{2}} {p}^{\mathrm{3}} \\ $$$${substitute}\:\left(\mathrm{2}\right)\:{in}\:\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:\frac{{x}^{\mathrm{6}} }{{q}^{\mathrm{6}} }+\frac{{y}^{\mathrm{6}} }{{p}^{\mathrm{6}} }\:=\frac{\mathrm{1}−{x}^{\mathrm{2}} {q}^{\mathrm{3}} −{y}^{\mathrm{2}} {p}^{\mathrm{3}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} }{{p}^{\mathrm{3}} {q}^{\mathrm{3}} } \\ $$$$ \\ $$
Commented by TawaTawa last updated on 08/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
