Question Number 80982 by Power last updated on 08/Feb/20
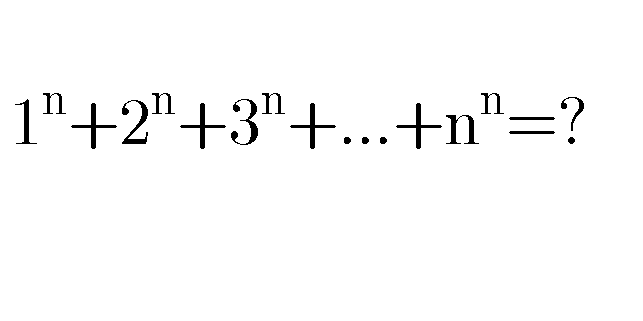
Commented by mr W last updated on 08/Feb/20

$$=\frac{\mathrm{2}}{\:\sqrt{{e}^{\pi} }}\beth\left(\zeta\left({n}\right)\right) \\ $$
Commented by mr W last updated on 08/Feb/20
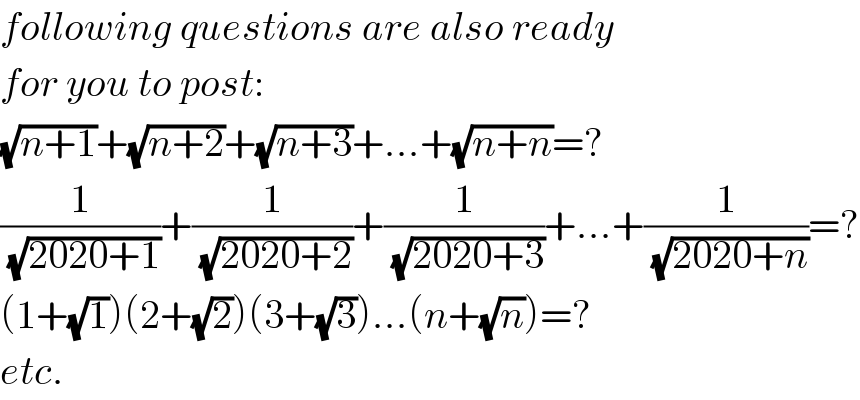
$${following}\:{questions}\:{are}\:{also}\:{ready} \\ $$$${for}\:{you}\:{to}\:{post}: \\ $$$$\sqrt{{n}+\mathrm{1}}+\sqrt{{n}+\mathrm{2}}+\sqrt{{n}+\mathrm{3}}+…+\sqrt{{n}+{n}}=? \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2020}+\mathrm{1}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2020}+\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2020}+\mathrm{3}}}+…+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2020}+{n}}}=? \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{1}}\right)\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\left(\mathrm{3}+\sqrt{\mathrm{3}}\right)…\left({n}+\sqrt{{n}}\right)=? \\ $$$${etc}. \\ $$
Commented by Power last updated on 08/Feb/20

$$\mathrm{solve}\:\mathrm{pls} \\ $$
