Question Number 80998 by Power last updated on 08/Feb/20

Commented by mr W last updated on 08/Feb/20

$${just}\:{as}\:{for}\:{a}\:{lot}\:{of}\:{your}\:{other}\:{questions}, \\ $$$${you}\:{also}\:{need}\:{a}\:{calculator}\:{for}\:{this}\:{one}. \\ $$
Answered by jagoll last updated on 09/Feb/20

$$\mathrm{tan}\:\mathrm{1}^{{o}} \:=\:\mathrm{tan}\:\left(\mathrm{90}^{{o}} −\mathrm{89}^{{o}} \right)\:=\:\mathrm{cot}\:\mathrm{89}^{{o}} \\ $$$$\mathrm{tan}\:\mathrm{1}^{{o}} +\mathrm{tan}\:\mathrm{89}^{{o}} \:=\:\mathrm{cot}\:\mathrm{89}^{{o}} +\mathrm{tan}\:\mathrm{89}^{{o}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{89}^{{o}} }\:+\:\mathrm{tan}\:\mathrm{89}^{{o}} \:=\:\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{89}^{{o}} }{\mathrm{tan}\:\mathrm{89}^{{o}} }\:=\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{89}^{{o}} }{\mathrm{tan}\:\mathrm{89}^{{o}} } \\ $$$${so}…{so}….= \\ $$
Commented by mr W last updated on 09/Feb/20

$${is}\:{it}\:{easier}\:{to}\:{calculate}\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{89}^{{o}} }{\mathrm{tan}\:\mathrm{89}^{{o}} }\:{than} \\ $$$${to}\:{calculate}\:\mathrm{tan}\:\mathrm{1}°+\mathrm{tan}\:\mathrm{89}°\:? \\ $$
Commented by john santu last updated on 09/Feb/20

$${there}\:{are}\:{times}\:{when}\:{an}\:{exam}\: \\ $$$${does}\:{not}\:{allow}\:{you}\:{to}\:{use}\:{a}\: \\ $$$${calculator} \\ $$
Commented by mr W last updated on 09/Feb/20

$${this}\:{is}\:{not}\:{a}\:{question}\:{from}\:{an}\:{exam}, \\ $$$${but}\:{one}\:{from}\:{Power}\:{sir}!\:{he}\:{has}\:{posted} \\ $$$${a}\:{lot}\:{of}\:{similar}\:{questions}\:{which}\:{have} \\ $$$${no}\:{smart}\:{solution}\:{but}\:{need}\:“{brute}−{force}''. \\ $$
Commented by $@ty@m123 last updated on 09/Feb/20

$${Just}\:{observe}\:{the}\:{types}\:{of}\:{question} \\ $$$${posted}\:{by}\:{Mr}.\:{Power}\:\&\:{you}\:{will} \\ $$$${understand}\:{what}\:{Mr}.\:{W}\:{means} \\ $$$${to}\:\:{say}. \\ $$$${Note}:\:{Mr}.\:{Power}\:{is}\:{a}\:{pseudo}\:{ID}. \\ $$$${Soon},\:{he}\:{will}\:{change}\:{his} \\ $$$${ID}. \\ $$$${But}\:{you}\:{can}\:{identify}\:{him}\:{from} \\ $$$${the}\:{type}\:{of}\:{questios}\:{posted}\:{by}\:{him}. \\ $$
Commented by john santu last updated on 09/Feb/20

$${is}\:{Mr}\:{Power}\:{old}\:{member}\:{in}\:{this} \\ $$$${forum}? \\ $$
Commented by $@ty@m123 last updated on 09/Feb/20
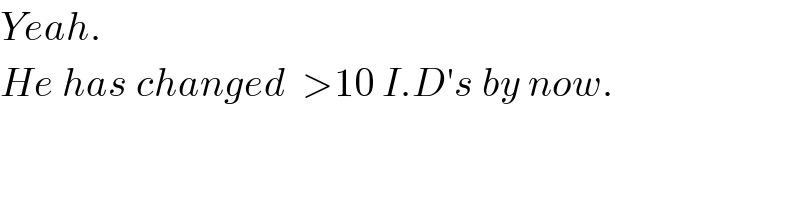
$${Yeah}. \\ $$$${He}\:{has}\:{changed}\:\:>\mathrm{10}\:{I}.{D}'{s}\:{by}\:{now}. \\ $$
Commented by mr W last updated on 09/Feb/20

$${sometimes}\:{he}\:{just}\:{uses}\:{an}\:{other}\:{ID} \\ $$$${to}\:{repost}\:{a}\:{question}\:{which}\:{he}\:{had} \\ $$$${repeated}\:{n}\:{times}\:{before}\:{and}\:{the}\:{answer} \\ $$$${is}\:{clearly}\:“{no}\:{solution}!''.\:{for}\:{this}\:{reason} \\ $$$${MJS}\:{sir}\:{has}\:{developed}\:{an}\:“{extented} \\ $$$${Martian}\:{integral}\:{second}\:{kind}''\:{especially} \\ $$$${for}\:{him}\:{and}\:{i}\:{devised}\:{newly}\:{also}\:{a}\:{special} \\ $$$${function}\:\beth\left(\zeta\left({n}\right)\right).\:{certainly}\:{both}\:{are} \\ $$$${not}\:{to}\:{find}\:{in}\:{any}\:{mathematics}\:{books}. \\ $$
