Menu Close

Question-81011

Tinku Tara 0 Comments
Pin




Question Number 81011 by mr W last updated on 08/Feb/20
Commented by mr W last updated on 08/Feb/20
A ball with mass m and radius r falls from a height of h and hits two wedges with mass M for each as shown. If the coefficient of restitution is e and the friction coefficient between wedges and ground is μ, find the distance the wedges move.
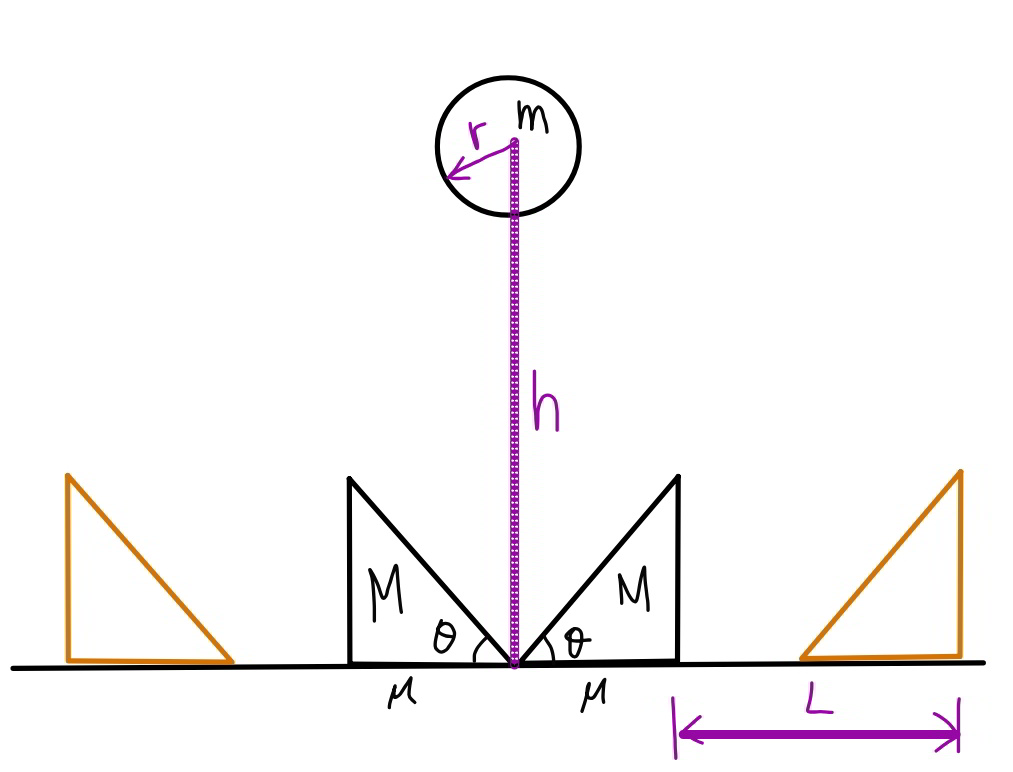
$${A}\:{ball}\:{with}\:{mass}\:{m}\:{and}\:{radius}\:{r}\:{falls} \\ $$$${from}\:{a}\:{height}\:{of}\:{h}\:{and}\:{hits}\:{two}\:{wedges} \\ $$$${with}\:{mass}\:{M}\:{for}\:{each}\:{as}\:{shown}. \\ $$$${If}\:{the}\:{coefficient}\:{of}\:{restitution}\:{is}\:{e} \\ $$$${and}\:{the}\:{friction}\:{coefficient}\:{between} \\ $$$${wedges}\:{and}\:{ground}\:{is}\:\mu,\:{find}\:{the} \\ $$$${distance}\:{the}\:{wedges}\:{move}. \\ $$
Commented by ajfour last updated on 09/Feb/20
Commented by ajfour last updated on 09/Feb/20
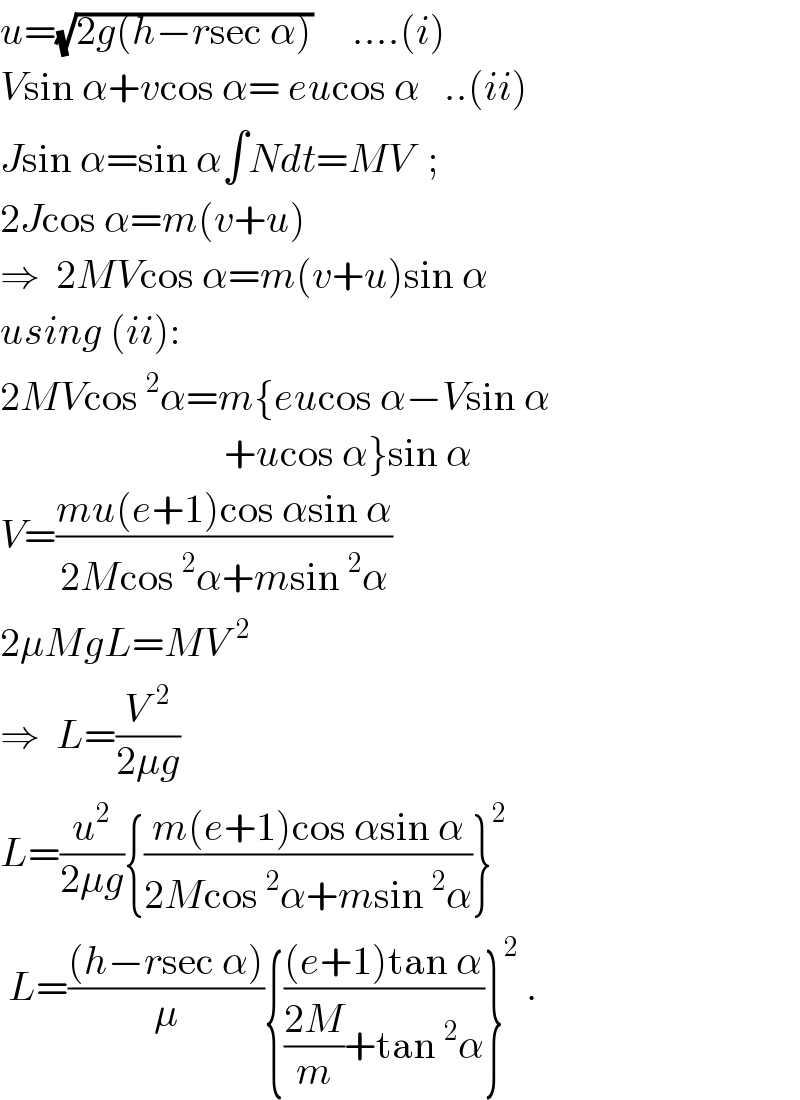
u=(√(2g(h−rsec α))) ....(i) Vsin α+vcos α= eucos α ..(ii) Jsin α=sin α∫Ndt=MV ; 2Jcos α=m(v+u) ⇒ 2MVcos α=m(v+u)sin α using (ii): 2MVcos^2 α=m{eucos α−Vsin α +ucos α}sin α V=((mu(e+1)cos αsin α)/(2Mcos^2 α+msin^2 α)) 2μMgL=MV^( 2) ⇒ L=(V^( 2) /(2μg)) L=(u^2 /(2μg)){((m(e+1)cos αsin α)/(2Mcos^2 α+msin^2 α))}^2 L=(((h−rsec α))/μ){(((e+1)tan α)/(((2M)/m)+tan^2 α))}^2 .
$${u}=\sqrt{\mathrm{2}{g}\left({h}−{r}\mathrm{sec}\:\alpha\right)}\:\:\:\:\:….\left({i}\right) \\ $$$${V}\mathrm{sin}\:\alpha+{v}\mathrm{cos}\:\alpha=\:{eu}\mathrm{cos}\:\alpha\:\:\:..\left({ii}\right) \\ $$$${J}\mathrm{sin}\:\alpha=\mathrm{sin}\:\alpha\int{Ndt}={MV}\:\:;\:\: \\ $$$$\mathrm{2}{J}\mathrm{cos}\:\alpha={m}\left({v}+{u}\right) \\ $$$$\Rightarrow\:\:\mathrm{2}{MV}\mathrm{cos}\:\alpha={m}\left({v}+{u}\right)\mathrm{sin}\:\alpha \\ $$$${using}\:\left({ii}\right): \\ $$$$\mathrm{2}{MV}\mathrm{cos}\:^{\mathrm{2}} \alpha={m}\left\{{eu}\mathrm{cos}\:\alpha−{V}\mathrm{sin}\:\alpha\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{u}\mathrm{cos}\:\alpha\right\}\mathrm{sin}\:\alpha \\ $$$${V}=\frac{{mu}\left({e}+\mathrm{1}\right)\mathrm{cos}\:\alpha\mathrm{sin}\:\alpha}{\mathrm{2}{M}\mathrm{cos}\:^{\mathrm{2}} \alpha+{m}\mathrm{sin}\:^{\mathrm{2}} \alpha} \\ $$$$\mathrm{2}\mu{MgL}={MV}^{\:\:\mathrm{2}} \\ $$$$\Rightarrow\:\:{L}=\frac{{V}^{\:\:\mathrm{2}} }{\mathrm{2}\mu{g}} \\ $$$${L}=\frac{{u}^{\mathrm{2}} }{\mathrm{2}\mu{g}}\left\{\frac{{m}\left({e}+\mathrm{1}\right)\mathrm{cos}\:\alpha\mathrm{sin}\:\alpha}{\mathrm{2}{M}\mathrm{cos}\:^{\mathrm{2}} \alpha+{m}\mathrm{sin}\:^{\mathrm{2}} \alpha}\right\}^{\mathrm{2}} \\ $$$$\:{L}=\frac{\left({h}−{r}\mathrm{sec}\:\alpha\right)}{\mu}\left\{\frac{\left({e}+\mathrm{1}\right)\mathrm{tan}\:\alpha}{\frac{\mathrm{2}{M}}{{m}}+\mathrm{tan}\:^{\mathrm{2}} \alpha}\right\}^{\mathrm{2}} \:. \\ $$
Commented by mr W last updated on 09/Feb/20
thanks alot sir! why is the momentum conservation in vertical direction not appliable?
$${thanks}\:{alot}\:{sir}! \\ $$$${why}\:{is}\:{the}\:{momentum}\:{conservation} \\ $$$${in}\:{vertical}\:{direction}\:{not}\:{appliable}? \\ $$
Commented by ajfour last updated on 09/Feb/20
while collision takes place, normal reaction from ground on wedges, increases substan- cially and back to Mg.
$${while}\:{collision}\:{takes}\:{place}, \\ $$$${normal}\:{reaction}\:{from}\:{ground} \\ $$$${on}\:{wedges},\:{increases}\:{substan}- \\ $$$${cially}\:{and}\:{back}\:{to}\:{Mg}. \\ $$
Commented by mr W last updated on 09/Feb/20
that′s it!
$${that}'{s}\:{it}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *