Question Number 81075 by ajfour last updated on 09/Feb/20
Commented by ajfour last updated on 09/Feb/20

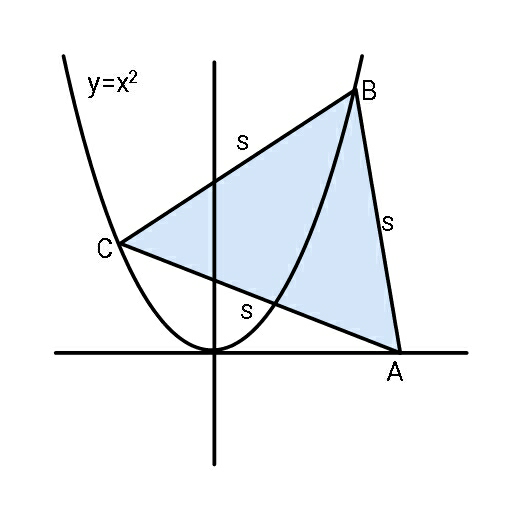
$${Given}\:{s},\:{find}\:{coordinates} \\ $$$${of}\:{A},{B},{C}. \\ $$
Answered by ajfour last updated on 09/Feb/20
![Let A(h,0) and let bisector of ∠A make an angle θ with −ve x-axis. B[h−scos (θ+(π/6)), ssin (θ+(π/6))] C[h−scos (θ−(π/6)), ssin (θ−(π/6))] ssin (θ+(π/6))={h−scos (θ+(π/6))}^2 ssin (θ−(π/6))={h−scos (θ−(π/6))}^2 ⇒ (√(sin (θ+(π/6))))−(√(sin (θ−(π/6)))) = (√s)[cos (θ−(π/6))−cos (θ+(π/6))] .........](https://www.tinkutara.com/question/Q81097.png)
$${Let}\:{A}\left({h},\mathrm{0}\right) \\ $$$${and}\:{let}\:{bisector}\:{of}\:\angle{A}\:{make} \\ $$$${an}\:{angle}\:\theta\:{with}\:−{ve}\:{x}-{axis}. \\ $$$${B}\left[{h}−{s}\mathrm{cos}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right),\:{s}\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)\right] \\ $$$${C}\left[{h}−{s}\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right),\:{s}\mathrm{sin}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)\right] \\ $$$${s}\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)=\left\{{h}−{s}\mathrm{cos}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)\right\}^{\mathrm{2}} \\ $$$${s}\mathrm{sin}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)=\left\{{h}−{s}\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)\right\}^{\mathrm{2}} \\ $$$$\Rightarrow\:\sqrt{\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)}−\sqrt{\mathrm{sin}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)} \\ $$$$\:\:=\:\sqrt{{s}}\left[\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)−\mathrm{cos}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)\right] \\ $$$$……… \\ $$
Commented by ajfour last updated on 09/Feb/20
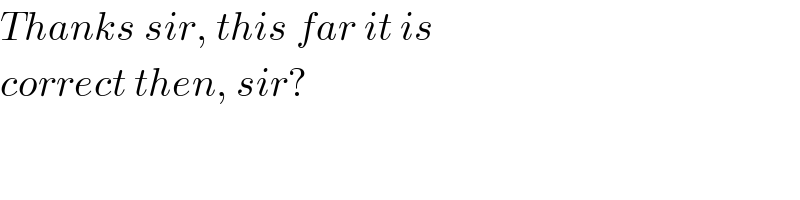
$${Thanks}\:{sir},\:{this}\:{far}\:{it}\:{is} \\ $$$${correct}\:{then},\:{sir}? \\ $$
Commented by mr W last updated on 09/Feb/20

$${independently}\:{from}\:{each}\:{other}\:{we} \\ $$$${had}\:{the}\:{same}\:{idea}\:{to}\:{use}\:{the}\:{bisector} \\ $$$${of}\:{angle}\:{A}\:{as}\:{parameter},\:{because}\:{we} \\ $$$${can}\:{get}\:{in}\:{this}\:{easy}\:{way}\:{an}\:{equation}\: \\ $$$${with}\:{only}\:{one}\:{variable}. \\ $$
Answered by mr W last updated on 09/Feb/20
![A(a,0) D(h,k) h=a−(((√3)s)/2) cos θ k=(((√3)s)/2) sin θ x_B =h+(s/2) sin θ y_B =k+(s/2) cos θ=(h+(s/2) sin θ)^2 (((√3)s)/2) sin θ+(s/2) cos θ=(a−(((√3)s)/2) cos θ+(s/2) sin θ)^2 let (a/s)=λ ((√3)/2) sin θ+(1/2) cos θ=s(λ−((√3)/2) cos θ+(1/2) sin θ)^2 cos (π/6) sin θ+sin (π/6) cos θ=s(λ−cos (π/6) cos θ+sin (π/6) sin θ)^2 ⇒sin (θ+(π/6))=s[λ−cos (θ+(π/6))]^2 ...(i) x_C =h−(s/2) sin θ y_C =k−(s/2) cos θ=(h−(s/2) sin θ)^2 (((√3)s)/2) sin θ−(s/2) cos θ=(a−(((√3)s)/2) cos θ−(s/2) sin θ)^2 ((√3)/2) sin θ−(1/2) cos θ=s(λ−((√3)/2) cos θ−(1/2) sin θ)^2 ⇒sin (θ−(π/6))=s[λ−cos (θ−(π/6))]^2 ...(ii) from (i) and (ii) we get: (((√(sin (θ+(π/6))))±(√(sin (θ−(π/6)))))/(cos (θ−(π/6))−cos (θ+(π/6))))=(√s) ......](https://www.tinkutara.com/question/Q81106.png)
$${A}\left({a},\mathrm{0}\right) \\ $$$${D}\left({h},{k}\right) \\ $$$${h}={a}−\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\mathrm{cos}\:\theta \\ $$$${k}=\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta \\ $$$${x}_{{B}} ={h}+\frac{{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta \\ $$$${y}_{{B}} ={k}+\frac{{s}}{\mathrm{2}}\:\mathrm{cos}\:\theta=\left({h}+\frac{{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta+\frac{{s}}{\mathrm{2}}\:\mathrm{cos}\:\theta=\left({a}−\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\mathrm{cos}\:\theta+\frac{{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$${let}\:\frac{{a}}{{s}}=\lambda \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{sin}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}\:\theta={s}\left(\lambda−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cos}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\mathrm{cos}\:\frac{\pi}{\mathrm{6}}\:\mathrm{sin}\:\theta+\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\:\mathrm{cos}\:\theta={s}\left(\lambda−\mathrm{cos}\:\frac{\pi}{\mathrm{6}}\:\mathrm{cos}\:\theta+\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)={s}\left[\lambda−\mathrm{cos}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)\right]^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$ \\ $$$${x}_{{C}} ={h}−\frac{{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta \\ $$$${y}_{{C}} ={k}−\frac{{s}}{\mathrm{2}}\:\mathrm{cos}\:\theta=\left({h}−\frac{{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta−\frac{{s}}{\mathrm{2}}\:\mathrm{cos}\:\theta=\left({a}−\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\mathrm{cos}\:\theta−\frac{{s}}{\mathrm{2}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{sin}\:\theta−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}\:\theta={s}\left(\lambda−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cos}\:\theta−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)={s}\left[\lambda−\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)\right]^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{get}: \\ $$$$\frac{\sqrt{\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)}\pm\sqrt{\mathrm{sin}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)}}{\mathrm{cos}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)−\mathrm{cos}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)}=\sqrt{{s}} \\ $$$$…… \\ $$
Commented by mr W last updated on 09/Feb/20
Commented by mr W last updated on 09/Feb/20
Commented by jagoll last updated on 09/Feb/20

$${great}\:! \\ $$
Commented by mr W last updated on 09/Feb/20
Commented by ajfour last updated on 09/Feb/20
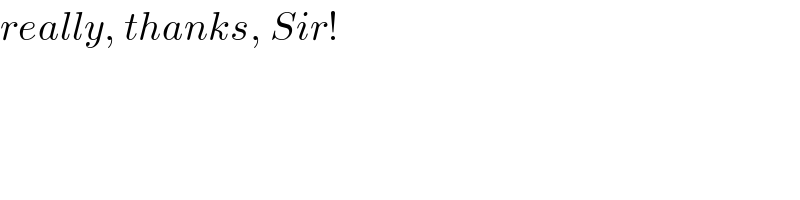
$${really},\:{thanks},\:{Sir}! \\ $$
Commented by mr W last updated on 09/Feb/20
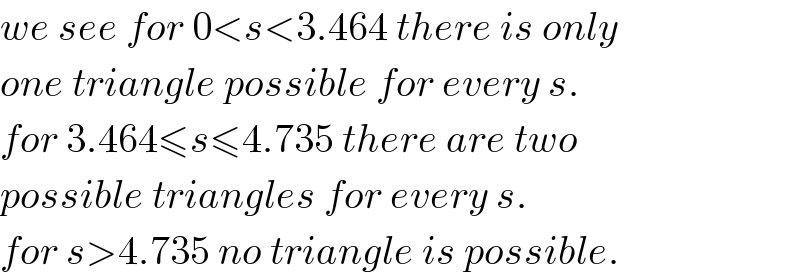
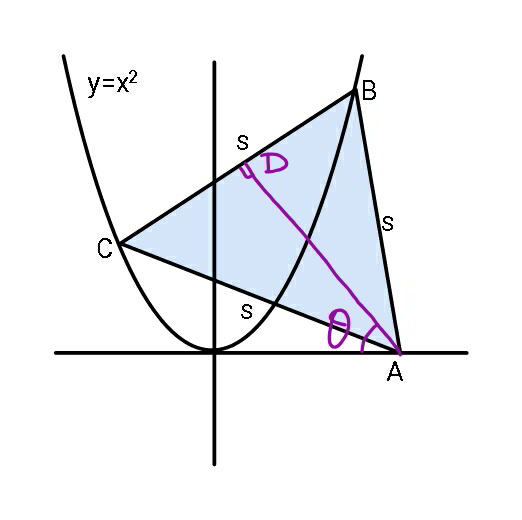
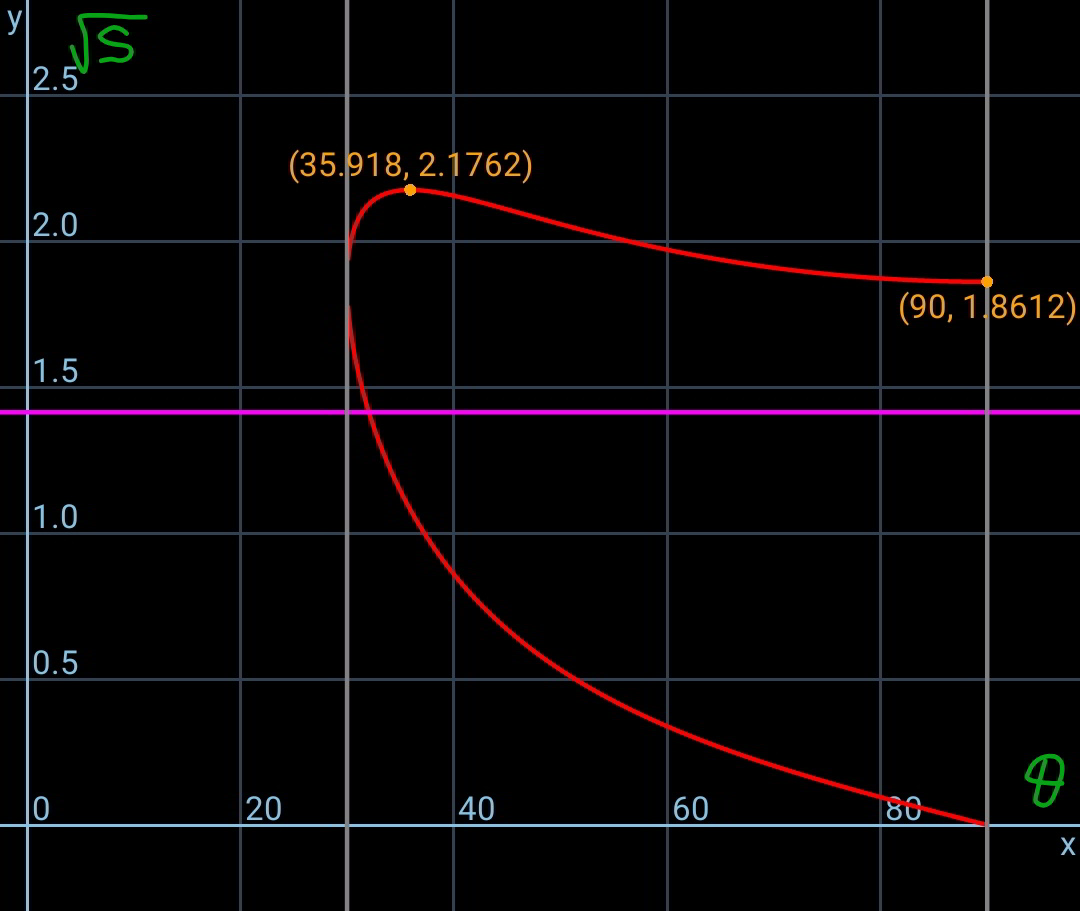
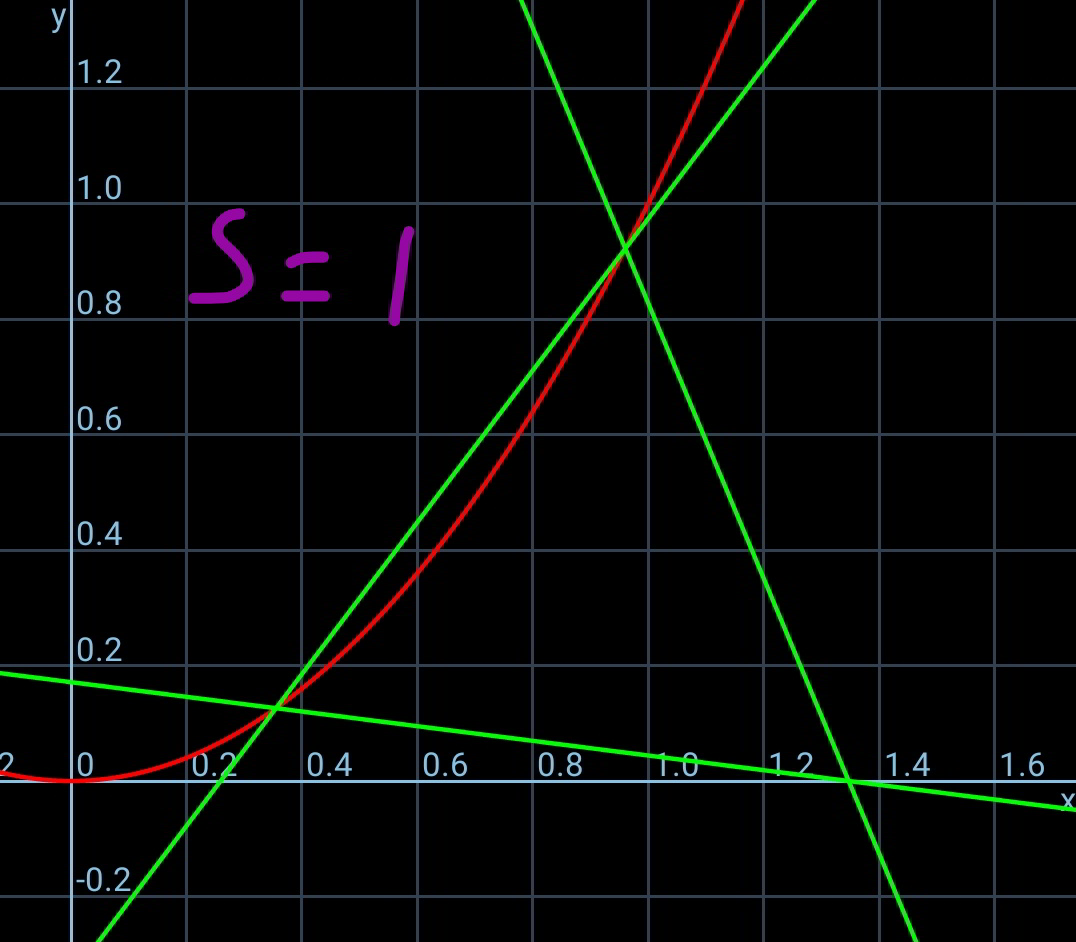
$${we}\:{see}\:{for}\:\mathrm{0}<{s}<\mathrm{3}.\mathrm{464}\:{there}\:{is}\:{only} \\ $$$${one}\:{triangle}\:{possible}\:{for}\:{every}\:{s}. \\ $$$${for}\:\mathrm{3}.\mathrm{464}\leqslant{s}\leqslant\mathrm{4}.\mathrm{735}\:{there}\:{are}\:{two} \\ $$$${possible}\:{triangles}\:{for}\:{every}\:{s}. \\ $$$${for}\:{s}>\mathrm{4}.\mathrm{735}\:{no}\:{triangle}\:{is}\:{possible}. \\ $$
Commented by ajfour last updated on 09/Feb/20
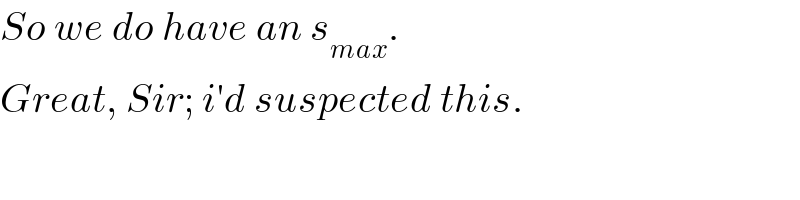
$${So}\:{we}\:{do}\:{have}\:{an}\:{s}_{{max}} . \\ $$$${Great},\:{Sir};\:{i}'{d}\:{suspected}\:{this}. \\ $$
