Question-81122

Question Number 81122 by mr W last updated on 09/Feb/20

Commented by mr W last updated on 09/Feb/20

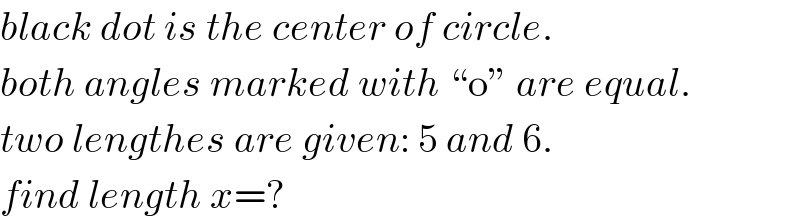
black dot is the center of circle. both angles marked with “o” are equal. two lengthes are given: 5 and 6. find length x=?

$${black}\:{dot}\:{is}\:{the}\:{center}\:{of}\:{circle}. \\ $$$${both}\:{angles}\:{marked}\:{with}\:“\mathrm{o}''\:{are}\:{equal}. \\ $$$${two}\:{lengthes}\:{are}\:{given}:\:\mathrm{5}\:{and}\:\mathrm{6}. \\ $$$${find}\:{length}\:{x}=? \\ $$

Commented by ajfour last updated on 09/Feb/20

Commented by ajfour last updated on 09/Feb/20

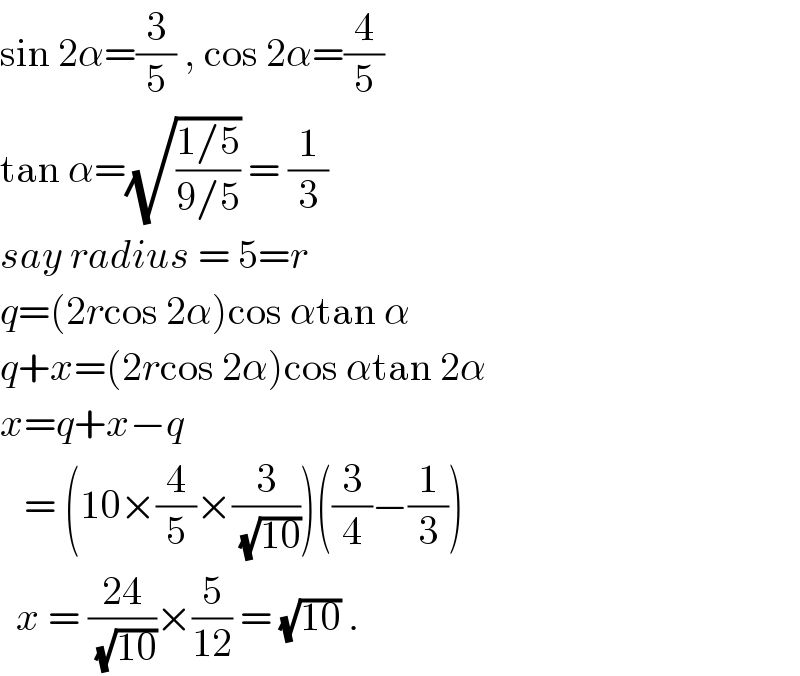
sin 2α=(3/5) , cos 2α=(4/5) tan α=(√((1/5)/(9/5))) = (1/3) say radius = 5=r q=(2rcos 2α)cos αtan α q+x=(2rcos 2α)cos αtan 2α x=q+x−q = (10×(4/5)×(3/( (√(10)))))((3/4)−(1/3)) x = ((24)/( (√(10))))×(5/(12)) = (√(10)) .

$$\mathrm{sin}\:\mathrm{2}\alpha=\frac{\mathrm{3}}{\mathrm{5}}\:,\:\mathrm{cos}\:\mathrm{2}\alpha=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{tan}\:\alpha=\sqrt{\frac{\mathrm{1}/\mathrm{5}}{\mathrm{9}/\mathrm{5}}}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${say}\:{radius}\:=\:\mathrm{5}={r} \\ $$$${q}=\left(\mathrm{2}{r}\mathrm{cos}\:\mathrm{2}\alpha\right)\mathrm{cos}\:\alpha\mathrm{tan}\:\alpha \\ $$$${q}+{x}=\left(\mathrm{2}{r}\mathrm{cos}\:\mathrm{2}\alpha\right)\mathrm{cos}\:\alpha\mathrm{tan}\:\mathrm{2}\alpha \\ $$$${x}={q}+{x}−{q} \\ $$$$\:\:\:=\:\left(\mathrm{10}×\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}\right)\left(\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\:\:{x}\:=\:\frac{\mathrm{24}}{\:\sqrt{\mathrm{10}}}×\frac{\mathrm{5}}{\mathrm{12}}\:=\:\sqrt{\mathrm{10}}\:. \\ $$

Commented by mr W last updated on 09/Feb/20

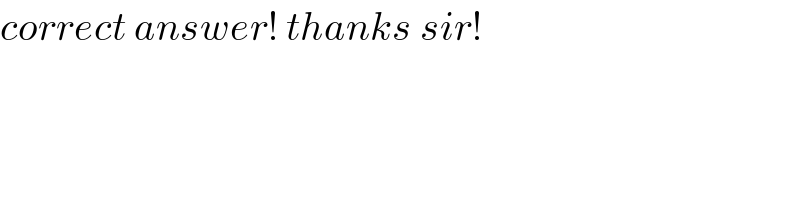
$${correct}\:{answer}!\:{thanks}\:{sir}! \\ $$

Answered by mr W last updated on 09/Feb/20

Commented by mr W last updated on 09/Feb/20

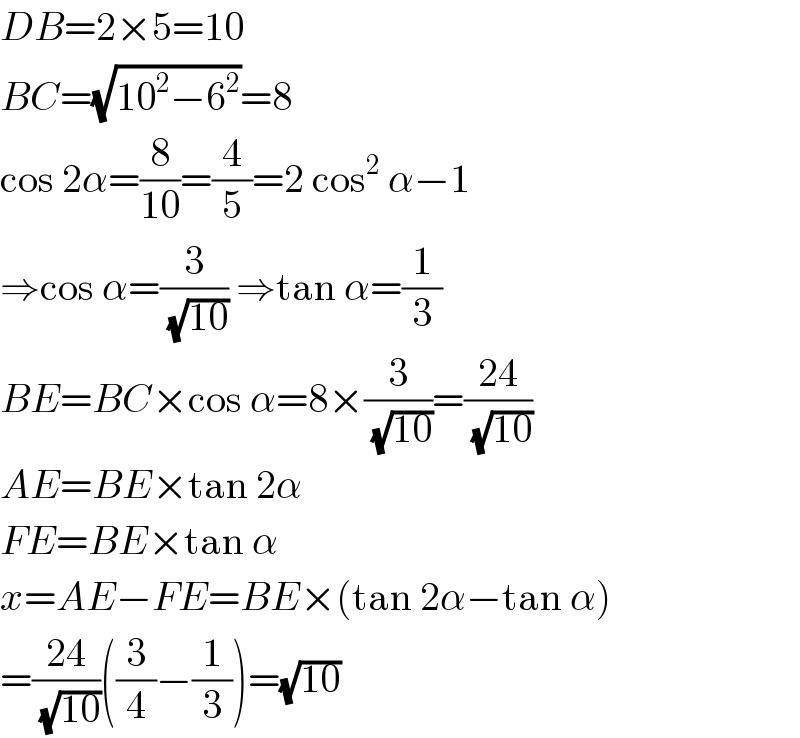
DB=2×5=10 BC=(√(10^2 −6^2 ))=8 cos 2α=(8/(10))=(4/5)=2 cos^2 α−1 ⇒cos α=(3/( (√(10)))) ⇒tan α=(1/3) BE=BC×cos α=8×(3/( (√(10))))=((24)/( (√(10)))) AE=BE×tan 2α FE=BE×tan α x=AE−FE=BE×(tan 2α−tan α) =((24)/( (√(10))))((3/4)−(1/3))=(√(10))

$${DB}=\mathrm{2}×\mathrm{5}=\mathrm{10} \\ $$$${BC}=\sqrt{\mathrm{10}^{\mathrm{2}} −\mathrm{6}^{\mathrm{2}} }=\mathrm{8} \\ $$$$\mathrm{cos}\:\mathrm{2}\alpha=\frac{\mathrm{8}}{\mathrm{10}}=\frac{\mathrm{4}}{\mathrm{5}}=\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}\:\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${BE}={BC}×\mathrm{cos}\:\alpha=\mathrm{8}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}=\frac{\mathrm{24}}{\:\sqrt{\mathrm{10}}} \\ $$$${AE}={BE}×\mathrm{tan}\:\mathrm{2}\alpha \\ $$$${FE}={BE}×\mathrm{tan}\:\alpha \\ $$$${x}={AE}−{FE}={BE}×\left(\mathrm{tan}\:\mathrm{2}\alpha−\mathrm{tan}\:\alpha\right) \\ $$$$=\frac{\mathrm{24}}{\:\sqrt{\mathrm{10}}}\left(\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\sqrt{\mathrm{10}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply