Question Number 81123 by M±th+et£s last updated on 09/Feb/20
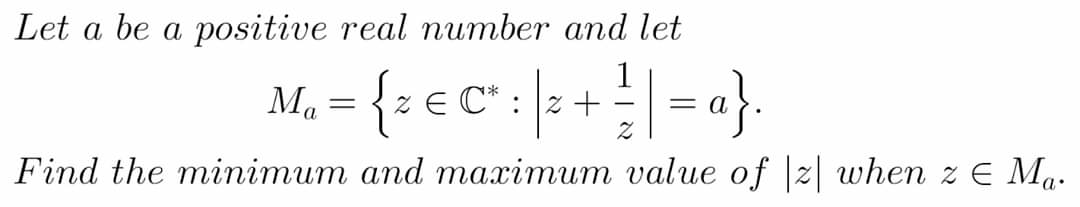
Commented by mr W last updated on 09/Feb/20

$${let}\:{z}={x}+{yi} \\ $$$$\mid{z}\mid=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${let}\:{P}=\mid{z}\mid^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${z}+\frac{\mathrm{1}}{{z}}={x}+{yi}+\frac{\mathrm{1}}{{x}+{yi}}={x}+{yi}+\frac{{x}−{yi}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$={x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)+{y}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right){i} \\ $$$$\mid{z}+\frac{\mathrm{1}}{{z}}\mid=\sqrt{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)^{\mathrm{2}} }={a} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left({P}+\mathrm{1}\right)^{\mathrm{2}} +\left({P}−{x}^{\mathrm{2}} \right)\left({P}−\mathrm{1}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {P}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}\left({P}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} \left({P}+\mathrm{1}\right)\frac{{dP}}{{dx}}+\left(\frac{{dP}}{{dx}}−\mathrm{2}{x}\right)\left({P}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\left({P}−{x}^{\mathrm{2}} \right)\left({P}−\mathrm{1}\right)\frac{{dP}}{{dx}}=\mathrm{2}{a}^{\mathrm{2}} {P}\frac{{dP}}{{dx}} \\ $$$${min}.\:{or}\:{max}.\:\mid{z}\mid\:\Rightarrow{min}.\:{or}\:{max}.\:{P}\:\Rightarrow\frac{{dP}}{{dx}}=\mathrm{0} \\ $$$$\mathrm{2}{x}\left({P}+\mathrm{1}\right)^{\mathrm{2}} +\left(−\mathrm{2}{x}\right)\left({P}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{8}{xP}=\mathrm{0} \\ $$$${P}\neq\mathrm{0}\:\Rightarrow{x}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \left({y}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${y}\neq\mathrm{0}\:\Rightarrow\left({y}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$${y}^{\mathrm{4}} −\left(\mathrm{2}+{a}^{\mathrm{2}} \right){y}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{2}+{a}^{\mathrm{2}} \pm{a}\sqrt{\mathrm{4}+{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${P}_{{min}} =\mathrm{0}^{\mathrm{2}} +\frac{\mathrm{2}+{a}^{\mathrm{2}} −{a}\sqrt{\mathrm{4}+{a}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\mathrm{2}+{a}^{\mathrm{2}} −{a}\sqrt{\mathrm{4}+{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${P}_{{max}} =\mathrm{0}^{\mathrm{2}} +\frac{\mathrm{2}+{a}^{\mathrm{2}} +{a}\sqrt{\mathrm{4}+{a}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\mathrm{2}+{a}^{\mathrm{2}} +{a}\sqrt{\mathrm{4}+{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow\mid{z}\mid_{{min}} =\sqrt{\frac{\mathrm{2}+{a}^{\mathrm{2}} −{a}\sqrt{\mathrm{4}+{a}^{\mathrm{2}} }}{\mathrm{2}}} \\ $$$$\Rightarrow\mid{z}\mid_{{max}} =\sqrt{\frac{\mathrm{2}+{a}^{\mathrm{2}} +{a}\sqrt{\mathrm{4}+{a}^{\mathrm{2}} }}{\mathrm{2}}} \\ $$
Commented by mr W last updated on 10/Feb/20
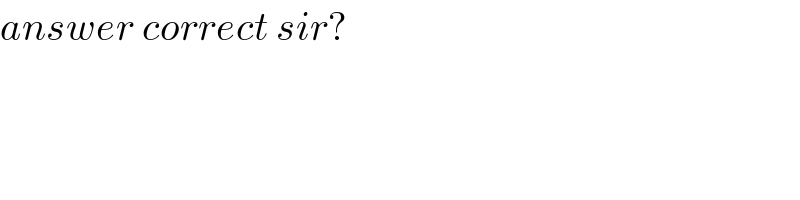
$${answer}\:{correct}\:{sir}? \\ $$
Commented by M±th+et£s last updated on 10/Feb/20
$${yes}\:{thank}\:{you}\:{nice}\:{work} \\ $$
