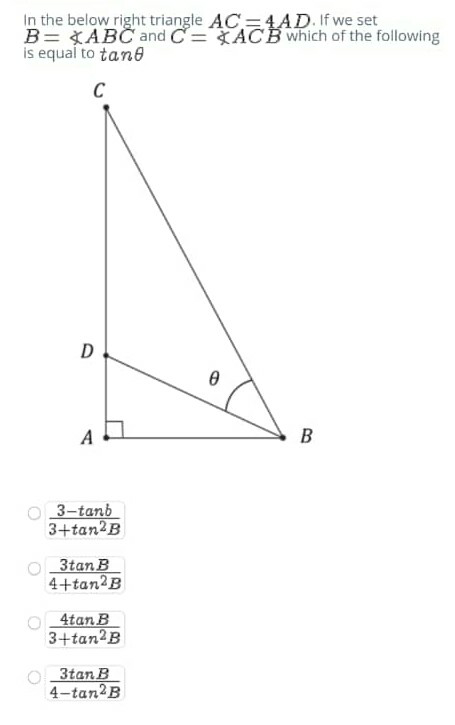
Question Number 81149 by TawaTawa last updated on 09/Feb/20
Answered by mind is power last updated on 09/Feb/20
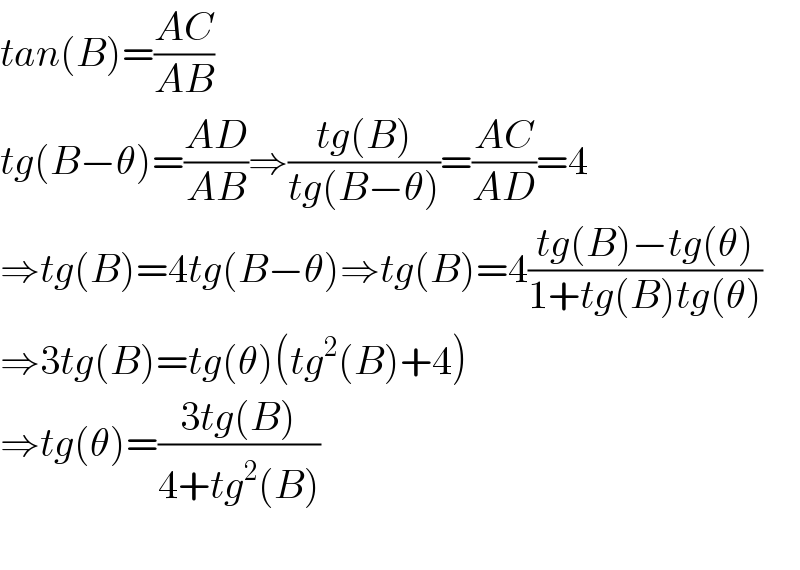
$${tan}\left({B}\right)=\frac{{AC}}{{AB}} \\ $$$${tg}\left({B}−\theta\right)=\frac{{AD}}{{AB}}\Rightarrow\frac{{tg}\left({B}\right)}{{tg}\left({B}−\theta\right)}=\frac{{AC}}{{AD}}=\mathrm{4} \\ $$$$\Rightarrow{tg}\left({B}\right)=\mathrm{4}{tg}\left({B}−\theta\right)\Rightarrow{tg}\left({B}\right)=\mathrm{4}\frac{{tg}\left({B}\right)−{tg}\left(\theta\right)}{\mathrm{1}+{tg}\left({B}\right){tg}\left(\theta\right)} \\ $$$$\Rightarrow\mathrm{3}{tg}\left({B}\right)={tg}\left(\theta\right)\left({tg}^{\mathrm{2}} \left({B}\right)+\mathrm{4}\right) \\ $$$$\Rightarrow{tg}\left(\theta\right)=\frac{\mathrm{3}{tg}\left({B}\right)}{\mathrm{4}+{tg}^{\mathrm{2}} \left({B}\right)} \\ $$$$ \\ $$
Commented by TawaTawa last updated on 09/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mind is power last updated on 09/Feb/20
$${withe}\:{pleasur}\:{miss} \\ $$
