Question Number 81188 by jagoll last updated on 10/Feb/20
Commented by jagoll last updated on 10/Feb/20

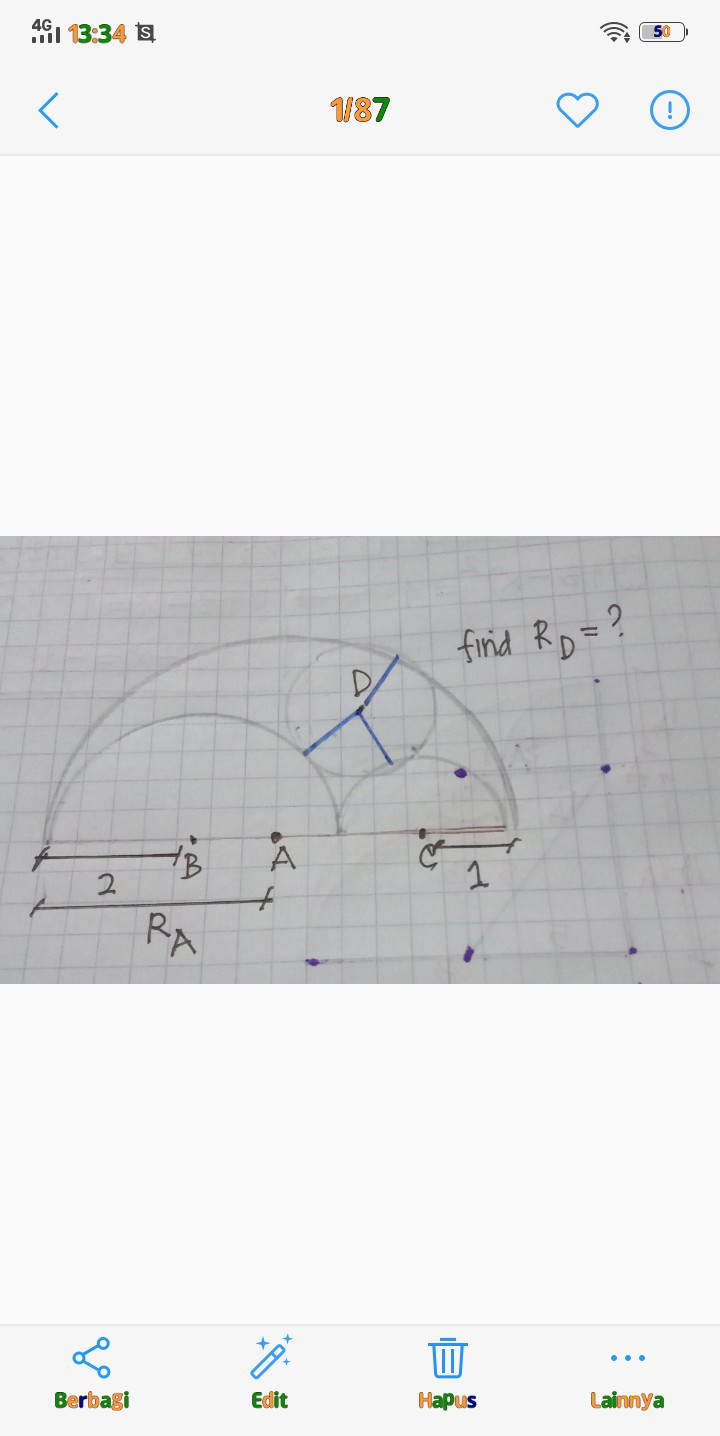
$${dear}\:{mr}\:{W} \\ $$
Answered by mr W last updated on 10/Feb/20

Commented by mr W last updated on 10/Feb/20
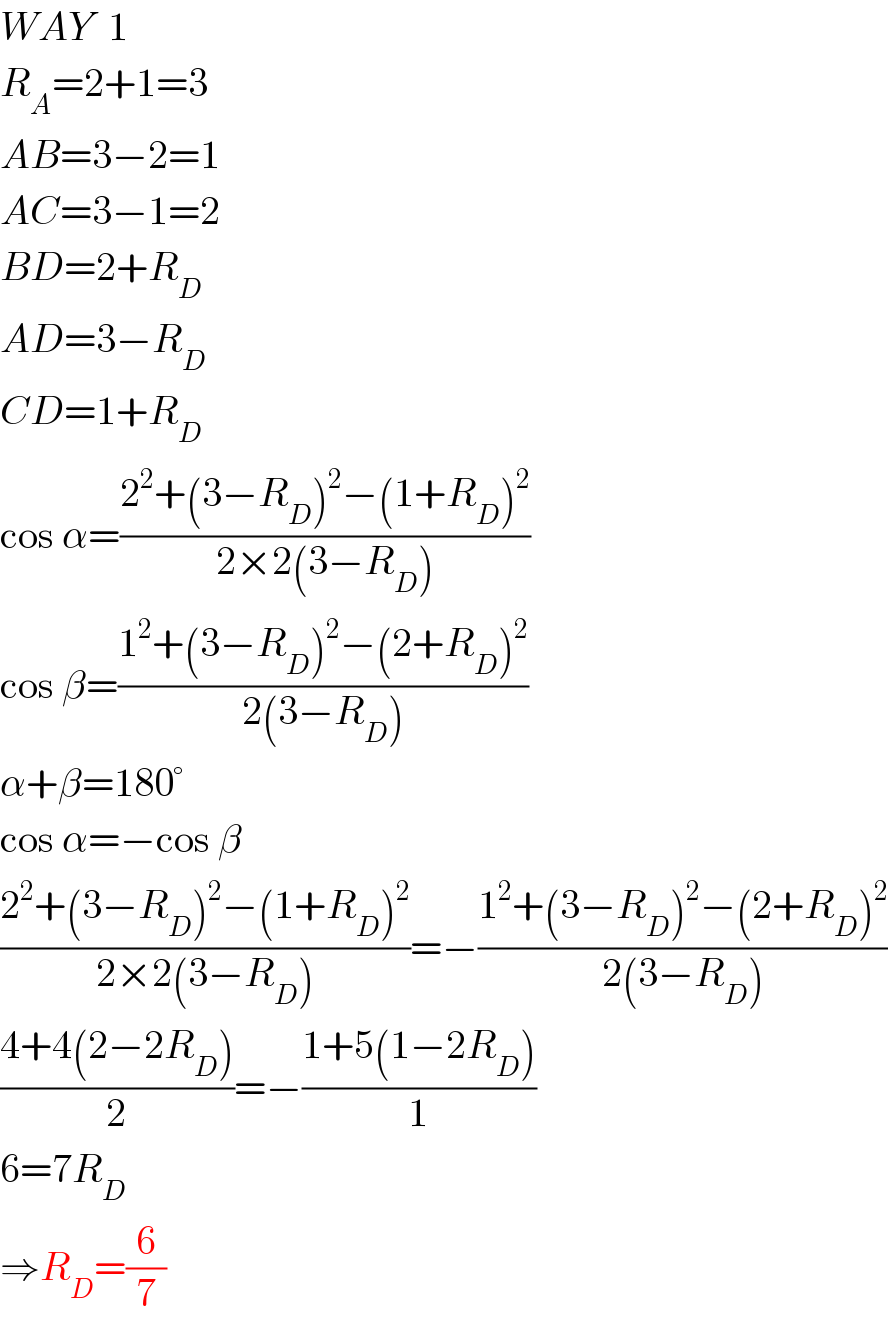
$${WAY}\:\:\mathrm{1} \\ $$$${R}_{{A}} =\mathrm{2}+\mathrm{1}=\mathrm{3} \\ $$$${AB}=\mathrm{3}−\mathrm{2}=\mathrm{1} \\ $$$${AC}=\mathrm{3}−\mathrm{1}=\mathrm{2} \\ $$$${BD}=\mathrm{2}+{R}_{{D}} \\ $$$${AD}=\mathrm{3}−{R}_{{D}} \\ $$$${CD}=\mathrm{1}+{R}_{{D}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{2}^{\mathrm{2}} +\left(\mathrm{3}−{R}_{{D}} \right)^{\mathrm{2}} −\left(\mathrm{1}+{R}_{{D}} \right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}\left(\mathrm{3}−{R}_{{D}} \right)} \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{1}^{\mathrm{2}} +\left(\mathrm{3}−{R}_{{D}} \right)^{\mathrm{2}} −\left(\mathrm{2}+{R}_{{D}} \right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{3}−{R}_{{D}} \right)} \\ $$$$\alpha+\beta=\mathrm{180}° \\ $$$$\mathrm{cos}\:\alpha=−\mathrm{cos}\:\beta \\ $$$$\frac{\mathrm{2}^{\mathrm{2}} +\left(\mathrm{3}−{R}_{{D}} \right)^{\mathrm{2}} −\left(\mathrm{1}+{R}_{{D}} \right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}\left(\mathrm{3}−{R}_{{D}} \right)}=−\frac{\mathrm{1}^{\mathrm{2}} +\left(\mathrm{3}−{R}_{{D}} \right)^{\mathrm{2}} −\left(\mathrm{2}+{R}_{{D}} \right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{3}−{R}_{{D}} \right)} \\ $$$$\frac{\mathrm{4}+\mathrm{4}\left(\mathrm{2}−\mathrm{2}{R}_{{D}} \right)}{\mathrm{2}}=−\frac{\mathrm{1}+\mathrm{5}\left(\mathrm{1}−\mathrm{2}{R}_{{D}} \right)}{\mathrm{1}} \\ $$$$\mathrm{6}=\mathrm{7}{R}_{{D}} \\ $$$$\Rightarrow{R}_{{D}} =\frac{\mathrm{6}}{\mathrm{7}} \\ $$
Commented by mr W last updated on 10/Feb/20
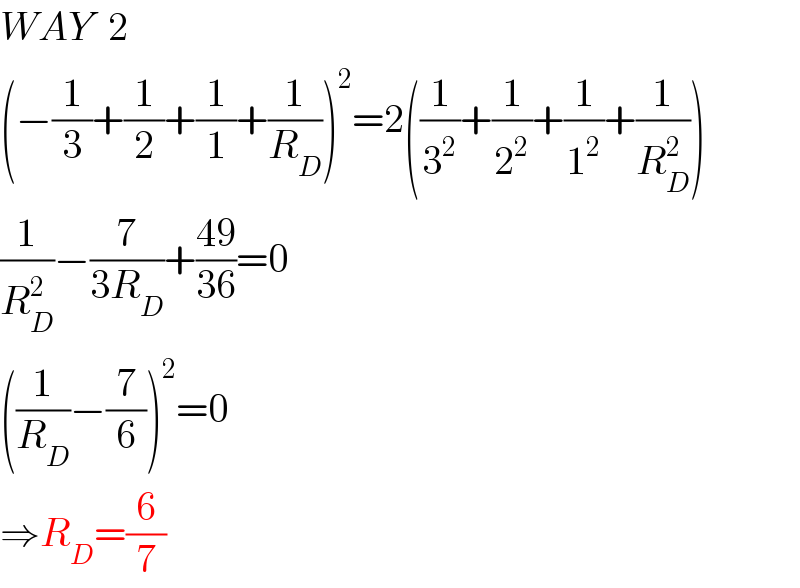
$${WAY}\:\:\mathrm{2} \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{{R}_{{D}} }\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}_{{D}} ^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{1}}{{R}_{{D}} ^{\mathrm{2}} }−\frac{\mathrm{7}}{\mathrm{3}{R}_{{D}} }+\frac{\mathrm{49}}{\mathrm{36}}=\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{{R}_{{D}} }−\frac{\mathrm{7}}{\mathrm{6}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{R}_{{D}} =\frac{\mathrm{6}}{\mathrm{7}} \\ $$
Commented by jagoll last updated on 10/Feb/20
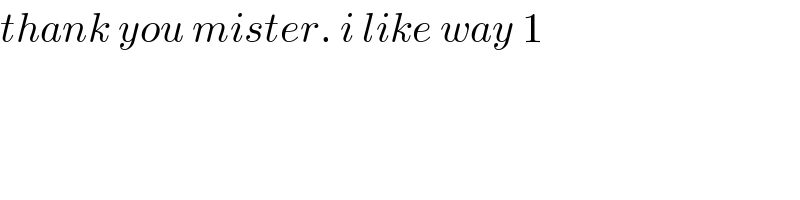
$${thank}\:{you}\:{mister}.\:{i}\:{like}\:{way}\:\mathrm{1} \\ $$
Answered by ajfour last updated on 10/Feb/20
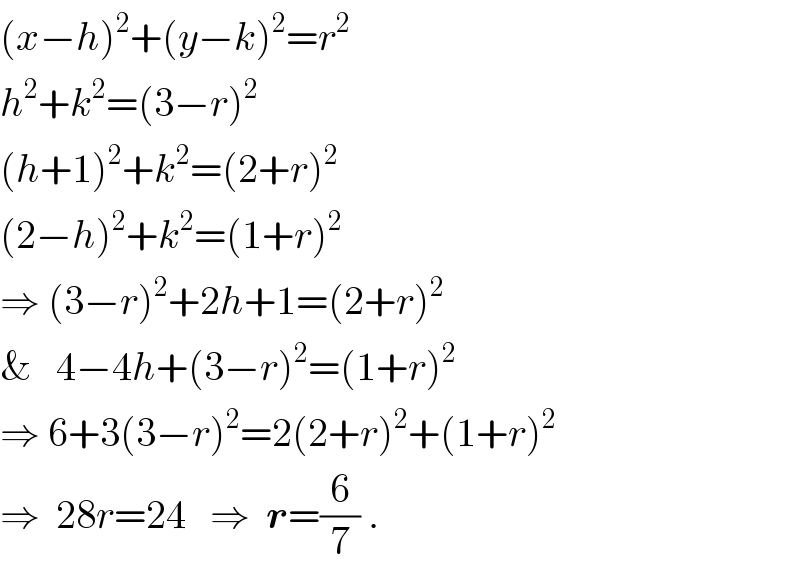
$$\left({x}−{h}\right)^{\mathrm{2}} +\left({y}−{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${h}^{\mathrm{2}} +{k}^{\mathrm{2}} =\left(\mathrm{3}−{r}\right)^{\mathrm{2}} \\ $$$$\left({h}+\mathrm{1}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} =\left(\mathrm{2}+{r}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2}−{h}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} =\left(\mathrm{1}+{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\left(\mathrm{3}−{r}\right)^{\mathrm{2}} +\mathrm{2}{h}+\mathrm{1}=\left(\mathrm{2}+{r}\right)^{\mathrm{2}} \\ $$$$\&\:\:\:\mathrm{4}−\mathrm{4}{h}+\left(\mathrm{3}−{r}\right)^{\mathrm{2}} =\left(\mathrm{1}+{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{6}+\mathrm{3}\left(\mathrm{3}−{r}\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{2}+{r}\right)^{\mathrm{2}} +\left(\mathrm{1}+{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{28}{r}=\mathrm{24}\:\:\:\Rightarrow\:\:\boldsymbol{{r}}=\frac{\mathrm{6}}{\mathrm{7}}\:. \\ $$
Commented by jagoll last updated on 10/Feb/20
$${thank}\:{you}\:{mister}\:.\:{great}.. \\ $$
