Question Number 81222 by M±th+et£s last updated on 10/Feb/20
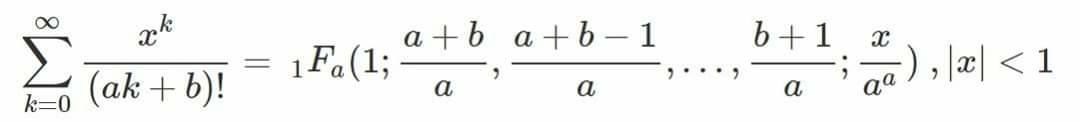
Answered by mind is power last updated on 10/Feb/20

$$\:\:_{\mathrm{1}} {F}_{{a}} \left(\mathrm{1};\frac{{a}+{b}}{{a}},\frac{{a}+{b}−\mathrm{1}}{{a}},…….,\frac{{b}+\mathrm{1}}{{a}};\frac{{x}}{{a}^{{a}} }\right) \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{k}!}{\underset{{j}=\mathrm{0}} {\overset{{a}−\mathrm{1}} {\prod}}\underset{{l}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left(\frac{{a}+{b}−{j}}{{a}}+{l}\right)}.\frac{{x}^{{k}} }{{a}^{{ak}} }.\frac{\mathrm{1}}{{k}!} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}} }{\underset{{j}=\mathrm{0}} {\overset{{a}−\mathrm{1}} {\prod}}\underset{{l}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left({a}+{b}−{j}+{al}\right).\frac{\mathrm{1}}{{a}^{{k}.{a}} }}.\frac{\mathrm{1}}{{a}^{{ka}} } \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}} }{\underset{{j}=\mathrm{0}} {\overset{{a}−\mathrm{1}} {\prod}}\underset{{l}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left({a}+{b}−{j}+{al}\right)}=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}} }{\underset{{l}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\underset{{j}=\mathrm{0}} {\overset{{a}−\mathrm{1}} {\prod}}\left({a}\left(\mathrm{1}+{l}\right)+{b}−{j}\right)} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}} }{\underset{{l}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\frac{\left({a}\left(\mathrm{1}+{l}\right)+{b}\right)!}{\left({al}+{b}\right)!}} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}} }{\underset{{l}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left({a}\left(\mathrm{1}+{l}\right)+{b}\right)!.\frac{\mathrm{1}}{\left({b}\right)!.\underset{{l}=\mathrm{0}} {\overset{{k}−\mathrm{2}} {\prod}}\left({a}\left({l}+\mathrm{1}\right)+{b}\right)!}} \\ $$$$\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{b}!{x}^{{k}} }{\left({ak}+{b}\right)!.}={b}!.\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{k}} }{\left({ak}+{b}\right)!}\:\:{ther}\:{is}\:{b}!\:\: \\ $$
Commented by M±th+et£s last updated on 11/Feb/20
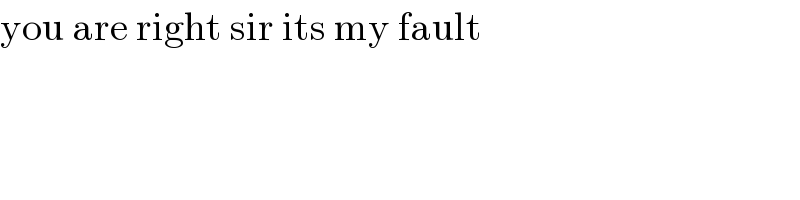
$$\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:\mathrm{sir}\:\mathrm{its}\:\mathrm{my}\:\mathrm{fault} \\ $$
