Question Number 81242 by panky0214 last updated on 10/Feb/20

Commented by mr W last updated on 10/Feb/20
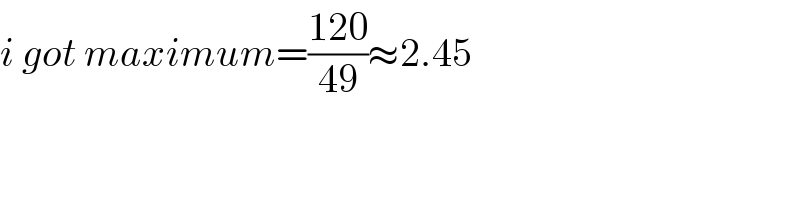
$${i}\:{got}\:{maximum}=\frac{\mathrm{120}}{\mathrm{49}}\approx\mathrm{2}.\mathrm{45} \\ $$
Commented by mr W last updated on 10/Feb/20
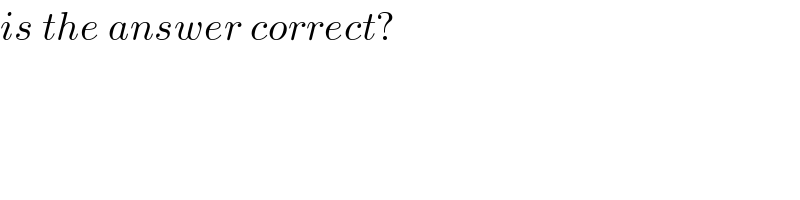
$${is}\:{the}\:{answer}\:{correct}? \\ $$
Commented by panky0214 last updated on 10/Feb/20
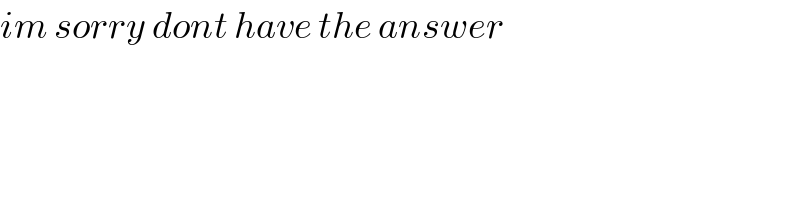
$${im}\:{sorry}\:{dont}\:{have}\:{the}\:{answer}\: \\ $$
Answered by mr W last updated on 10/Feb/20
![we have ten men, their names are cos x_k (k=1,2,...,10), or M_k for short. each of them can carry a number from −1 to +1. the sum of these numbers is zero. if n men carry positive numbers whose sum is T, then the other 10−n men carry negative numbers whose sum is −T. Σ_(k=1) ^n M_k =T Σ_(k=n+1) ^(10) M_k =−T now the numbers will be cubed. the positive numbers remain positive and the negative numbers remain negative. the sum of all is S. S=Σ_(k=1) ^(10) cos^3 x_k =S_P +S_N S_P =Σ_(k=1) ^n cos^3 x_k =Σ_(k=1) ^n M_k ^3 S_N =Σ_(k=n+1) ^(10) cos^3 x_k =Σ_(k=n+1) ^(10) M_k ^3 such that S is maximum, S_P should be as great as possible and S_N as small as possible. since Σ_(k=1) ^n M_k =T, the maximum of Σ_(k=1) ^n M_k ^3 is when M_k are equal and =(T/n). S_(P,max) =n((T/n))^3 similarly S_(N,min) =−(10−n)((T/(10−n)))^3 ⇒S_(max) =n((T/n))^3 −(10−n)((T/(10−n)))^3 let T=np with p≤1 ⇒S_(max) =n[1−(n^2 /((10−n)^2 ))]p^3 we see p=1 makes S_(max) maximum. ⇒S_(max) =n[1−(n^2 /((10−n)^2 ))] n=3 makes S_(max) maximum. ⇒S_(max) =3[1−(3^2 /7^2 )]=((120)/(49))≈2.45 that means Σ_(k=1) ^(10) cos^3 x_k reaches its maximum ((120)/(49)) when three from cos x_k take the value 1 for each and the other seven take −(3/7) for each.](https://www.tinkutara.com/question/Q81264.png)
$${we}\:{have}\:{ten}\:{men},\:{their}\:{names}\:{are} \\ $$$$\mathrm{cos}\:{x}_{{k}} \:\left({k}=\mathrm{1},\mathrm{2},…,\mathrm{10}\right),\:{or}\:{M}_{{k}} \:{for}\:{short}. \\ $$$${each}\:{of}\:{them}\:{can}\:{carry}\:{a}\:{number}\:{from} \\ $$$$−\mathrm{1}\:{to}\:+\mathrm{1}. \\ $$$${the}\:{sum}\:{of}\:{these}\:{numbers}\:{is}\:{zero}.\:{if} \\ $$$${n}\:{men}\:{carry}\:{positive}\:{numbers}\:{whose} \\ $$$${sum}\:{is}\:{T},\:{then}\:{the}\:{other}\:\mathrm{10}−{n}\:{men} \\ $$$${carry}\:{negative}\:{numbers}\:{whose}\:{sum} \\ $$$${is}\:−{T}. \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{M}_{{k}} ={T} \\ $$$$\underset{{k}={n}+\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{M}_{{k}} =−{T} \\ $$$${now}\:{the}\:{numbers}\:{will}\:{be}\:{cubed}.\:{the} \\ $$$${positive}\:{numbers}\:{remain}\:{positive} \\ $$$${and}\:{the}\:{negative}\:{numbers}\:{remain} \\ $$$${negative}.\:{the}\:{sum}\:{of}\:{all}\:{is}\:{S}. \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\mathrm{cos}^{\mathrm{3}} \:{x}_{{k}} ={S}_{{P}} +{S}_{{N}} \\ $$$${S}_{{P}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}^{\mathrm{3}} \:{x}_{{k}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{M}_{{k}} ^{\mathrm{3}} \\ $$$${S}_{{N}} =\underset{{k}={n}+\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\mathrm{cos}^{\mathrm{3}} \:{x}_{{k}} =\underset{{k}={n}+\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{M}_{{k}} ^{\mathrm{3}} \\ $$$${such}\:{that}\:{S}\:{is}\:{maximum},\:{S}_{{P}} \:{should} \\ $$$${be}\:{as}\:{great}\:{as}\:{possible}\:{and}\:{S}_{{N}} \:{as}\:{small} \\ $$$${as}\:{possible}. \\ $$$${since}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{M}_{{k}} ={T},\:{the}\:{maximum}\:{of}\: \\ $$$$\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{M}_{{k}} ^{\mathrm{3}} \:{is}\:{when}\:{M}_{{k}} \:{are}\:{equal}\:{and}\:=\frac{{T}}{{n}}. \\ $$$${S}_{{P},{max}} ={n}\left(\frac{{T}}{{n}}\right)^{\mathrm{3}} \\ $$$${similarly} \\ $$$${S}_{{N},{min}} =−\left(\mathrm{10}−{n}\right)\left(\frac{{T}}{\mathrm{10}−{n}}\right)^{\mathrm{3}} \\ $$$$\Rightarrow{S}_{{max}} ={n}\left(\frac{{T}}{{n}}\right)^{\mathrm{3}} −\left(\mathrm{10}−{n}\right)\left(\frac{{T}}{\mathrm{10}−{n}}\right)^{\mathrm{3}} \\ $$$${let}\:{T}={np}\:{with}\:{p}\leqslant\mathrm{1} \\ $$$$\Rightarrow{S}_{{max}} ={n}\left[\mathrm{1}−\frac{{n}^{\mathrm{2}} }{\left(\mathrm{10}−{n}\right)^{\mathrm{2}} }\right]{p}^{\mathrm{3}} \\ $$$${we}\:{see}\:{p}=\mathrm{1}\:{makes}\:{S}_{{max}} \:{maximum}. \\ $$$$\Rightarrow{S}_{{max}} ={n}\left[\mathrm{1}−\frac{{n}^{\mathrm{2}} }{\left(\mathrm{10}−{n}\right)^{\mathrm{2}} }\right] \\ $$$${n}=\mathrm{3}\:{makes}\:{S}_{{max}} \:{maximum}. \\ $$$$\Rightarrow{S}_{{max}} =\mathrm{3}\left[\mathrm{1}−\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{7}^{\mathrm{2}} }\right]=\frac{\mathrm{120}}{\mathrm{49}}\approx\mathrm{2}.\mathrm{45} \\ $$$${that}\:{means}\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\mathrm{cos}^{\mathrm{3}} \:{x}_{{k}} \:{reaches}\:{its} \\ $$$${maximum}\:\frac{\mathrm{120}}{\mathrm{49}}\:{when}\:{three}\:{from}\:\mathrm{cos}\:{x}_{{k}} \\ $$$${take}\:{the}\:{value}\:\mathrm{1}\:{for}\:{each}\:{and}\:{the}\:{other} \\ $$$${seven}\:{take}\:−\frac{\mathrm{3}}{\mathrm{7}}\:{for}\:{each}. \\ $$
Commented by mr W last updated on 10/Feb/20
![if we had 100 times cos x_k , then ⇒S_(max) =n[1−(n^2 /((100−n)^2 ))] with n=33 ⇒S_(max) =33[1−((33^2 )/(67^2 ))]=((112200)/(4489))≈24.994](https://www.tinkutara.com/question/Q81265.png)
$${if}\:{we}\:{had}\:\mathrm{100}\:{times}\:\mathrm{cos}\:{x}_{{k}} ,\:{then} \\ $$$$\Rightarrow{S}_{{max}} ={n}\left[\mathrm{1}−\frac{{n}^{\mathrm{2}} }{\left(\mathrm{100}−{n}\right)^{\mathrm{2}} }\right]\:{with}\:{n}=\mathrm{33} \\ $$$$\Rightarrow{S}_{{max}} =\mathrm{33}\left[\mathrm{1}−\frac{\mathrm{33}^{\mathrm{2}} }{\mathrm{67}^{\mathrm{2}} }\right]=\frac{\mathrm{112200}}{\mathrm{4489}}\approx\mathrm{24}.\mathrm{994} \\ $$
